非线性解方程组c语言_08 -- 非线性有限元分析方法

最新推荐文章于 2024-04-24 08:15:00 发布

草莓味的真知棒

最新推荐文章于 2024-04-24 08:15:00 发布

阅读量723

点赞数

文章标签：非线性解方程组c语言

本文链接：https://blog.csdn.net/weixin_32121931/article/details/113330906

版权

到目前为止，讨论的都是线性问题，这里采用了两个基本假设：

（1）材料的应力-应变关系是线性的，{σ}=[D]{ε}

（2）结构的应变-位移关系是线性的，{ε}=[B]{δ}

非线性有限元分析方法大同小异，以材料非线性为例：

（1）当材料的应力-应变关系是非线性时，刚度矩阵不是常数，与位移值有关，可记为：[K(δ)]

（2）此时，结构的整体平衡方程为：{Ψ}=[K(δ)]{δ}-{P}=0

增量法

采用增量法分析非线性问题时，把荷载划分为许多荷载增量，这些增量可以相等，也可以不等。每次施加一个荷载增量，在每一步计算中，假定方程是线性的，刚度矩阵[K]是常数。在不同的荷载增量中，刚度矩阵可以具有不同的数值，并与应力-应变关系相对应。每步施加一个荷载增量{△P}，得到一个位移增量{△δ}，累积后即得到位移{δ}。

增量法是用一系列线性问题去近似非线性问题，实质上是用分段线性的折线去代替非线性曲线。

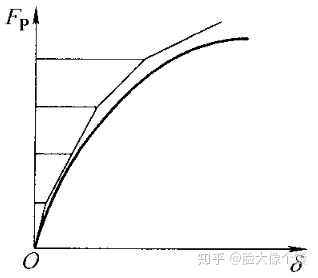
把荷载分为n个增量，所以总荷载为：

$equation?tex=%5Cleft%5C%7B+P+%5Cright%5C%7D%3D%5Csum_%7Bj%3D1%7D%5E%7Bn%7D%7B%5CDelta+P_%7Bj%7D%7D$

在施加第i个荷载增量后，荷载为：

$equation?tex=%5Cleft%5C%7B+P_%7Bi%7D+%5Cright%5C%7D%3D%5Csum_%7Bj%3D1%7D%5E%7Bi%7D%7B%5CDelta+P_%7Bj%7D%7D$

每一个荷载增量

$equation?tex=%5Cleft%5C%7B+%5CDelta+P_%7Bj%7D+%5Cright%5C%7D$ 产生一个位移增量

$equation?tex=%5Cleft%5C%7B+%5CDelta+%5Cdelta_%7Bj%7D+%5Cright%5C%7D$ 和应力增量

$equation?tex=%5Cleft%5C%7B+%5CDelta+%5Csigma_%7Bj%7D+%5Cright%5C%7D$ ，因此在施加第i个荷载增量后，位移和应力分别为：

$equation?tex=%5Cleft%5C%7B+%5Cdelta_%7Bi%7D+%5Cright%5C%7D%3D%5Csum_%7Bj%3D1%7D%5E%7Bi%7D%7B%5CDelta+%5Cdelta_%7Bj%7D%7D$

$equation?tex=%5Cleft%5C%7B+%5Csigma_%7Bi%7D+%5Cright%5C%7D%3D%5Csum_%7Bj%3D1%7D%5E%7Bi%7D%7B%5CDelta+%5Csigma_%7Bj%7D%7D$

至于如何由荷载增量

$equation?tex=%5Cleft%5C%7B+%5CDelta+P_%7Bi%7D+%5Cright%5C%7D$ 计算位移增量

$equation?tex=%5Cleft%5C%7B+%5CDelta+%5Cdelta_%7Bi%7D+%5Cright%5C%7D$ 和应力增量

$equation?tex=%5Cleft%5C%7B+%5CDelta+%5Csigma_%7Bi%7D+%5Cright%5C%7D$ ，有以下几种不同的方法。

一、始点刚度法

设第i-1步末的应力

$equation?tex=%5Cleft%5C%7B+%5CDelta+%5Csigma_%7Bi-1%7D+%5Cright%5C%7D$ 已求出，结合应力-应变关系可以确定第i-1步末的弹性矩阵

$equation?tex=%5Cleft%5B+D_%7Bi-1%7D+%5Cright%5D$ ，从而可以计算出第i-1步末的刚度矩阵

$equation?tex=%5Cleft%5B+K_%7Bi-1%7D+%5Cright%5D$ 。然后，假定在第i步内的刚度矩阵保持不变并近似地等于

$equation?tex=%5Cleft%5B+K_%7Bi-1%7D+%5Cright%5D$ ，于是，由下列方程可计算出第i步的位移增量

$equation?tex=%5Cleft%5C%7B+%5CDelta+%5Cdelta_%7Bi%7D+%5Cright%5C%7D$ ：

$equation?tex=%5Cleft%5C%7B+%5CDelta+%5Cvarepsilon_%7Bi%7D+%5Cright%5C%7D%3D%5Cleft%5B+B_%7Bi%7D+%5Cright%5D%5Cleft%5C%7B+%5CDelta+%5Cdelta_%7Bi%7D+%5Cright%5C%7D$

$equation?tex=%5Cleft%5C%7B+%5CDelta+%5Csigma_%7Bi%7D+%5Cright%5C%7D%3D%5Cleft%5B+D_%7Bi%7D+%5Cright%5D%5Cleft%5C%7B+%5CDelta+%5Cvarepsilon_%7Bi%7D+%5Cright%5C%7D$

$equation?tex=%5Cleft%5C%7B+%5Cdelta_%7Bi%7D+%5Cright%5C%7D%3D%5Cleft%5C%7B+%5Cdelta_%7Bi-1%7D+%5Cright%5C%7D%2B%5Cleft%5C%7B+%5CDelta+%5Cdelta_%7Bi%7D+%5Cright%5C%7D$

$equation?tex=%5Cleft%5C%7B+%5Csigma_%7Bi%7D+%5Cright%5C%7D%3D%5Cleft%5C%7B%5Csigma_%7Bi-1%7D+%5Cright%5C%7D%2B%5Cleft%5C%7B+%5CDelta+%5Csigma_%7Bi%7D+%5Cright%5C%7D$

根据第i步的总应力

$equation?tex=%5Cleft%5C%7B+%5Csigma_%7Bi%7D+%5Cright%5C%7D$ ，修正材料弹性常数，求出相应的单元刚度矩阵和整体刚度矩阵

$equation?tex=%5Cleft%5B+K_%7Bi%7D+%5Cright%5D$ ，准备施加下一步荷载增量

$equation?tex=%5Cleft%5C%7B+%5CDelta+P_%7Bi%2B1%7D+%5Cright%5C%7D$ 。

如果是最后一级荷载，则结束运算；如果不是，则进行下一步计算。

如果

$equation?tex=%5Cleft%5C%7B+%5Cdelta_%7Bi%7D+%5Cright%5C%7D$ 是精确解的话，应该满足下式：

{Ψ}=[K(δ)]{δ}-{P}=0

而实际上

$equation?tex=%5Cleft%5C%7B+%5Cdelta_%7Bi%7D+%5Cright%5C%7D$ 只是近似解，带入上式后有：

最低0.47元/天解锁文章

草莓味的真知棒

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
非线性解方程组c语言_08 -- 非线性有限元分析方法

到目前为止，讨论的都是线性问题，这里采用了两个基本假设：（1）材料的应力-应变关系是线性的，{σ}=[D]{ε}（2）结构的应变-位移关系是线性的，{ε}=[B]{δ}非线性有限元分析方法大同小异，以材料非线性为例：（1）当材料的应力-应变关系是非线性时，刚度矩阵不是常数，与位移值有关，可记为：[K(δ)]（2）此时，结构的整体平衡方程为：{Ψ}=[K(δ)]{δ}-{P}=0增量法采用增量法分析...
复制链接

扫一扫