十类方法,突破三角函数最值问题
三角函数的最值问题始终是三角函数中的热点问题之一,所涉及的知识广泛,综合性、灵活性较强。解决三角函数的最值问题,不仅会用到三角函数的定义、单调性、奇偶性、周期性、对称性、有界性,而且还会用到三角函数的恒等变换;同时,在三角函数的最值问题中常常涉及到初等函数、不等式、方程、几何等方面问题;
一、常用公式

下面具体介绍十类解题方法
题型一、y=asinx+b 或 y=acosx+b


题型二、y=asinx+bcosx型


题型三、转化二次函数(配方法)

若函数表达式中只含有正弦函数或余弦函数,且它们次数是2时,一般就需要通过配方或换元将给定的函数化归为二次函数的最值问题来处理.

题型四、引入参数转化(换元法)
对于一些比较复杂的复合三角函数,直接运用三角公式转化比较困难。针对题型结构特点,可以通过变量替换,将原来的三角问题转化为代数问题。这样就将比较复杂的函数转化为更容易求最值的代数函数求解。




题型五、基本不等式法
对于一些满足均值不等式特征结构的三角函数,可以运用均值不等式来解决此种类型的三角函数最值问题。均值不等式的一般形式:
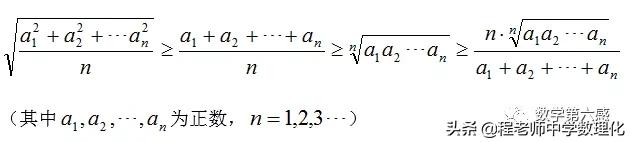
在运用均值不等式时,必须注意函数式中各项的正负,需要各项满足正值时方可使用,在解题时应加以论述说明;然后应该注意不等式中等号成立的条件、需要合理的拆添项,凑常数,以及不等式中和的最值与积的最值,

题型六、利用函数在区间内的单调性

题型七、转化为分式型



题型八、数形结合

题型九、判别法


题型十、分类讨论
含参数的三角函数的值域问题,需要对参数进行讨论.


课后作业

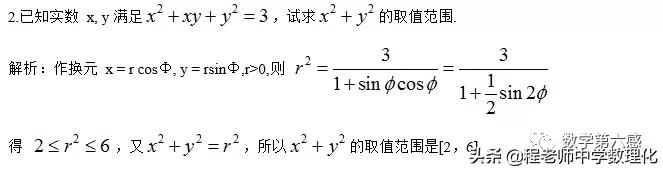
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








