离散数学教学课件完整指南

本文还有配套的精品资源，点击获取

简介：离散数学是计算机科学的基础课程，它涉及算法设计、数据结构、逻辑推理等多个核心领域。本课件基于耿素云和屈婉玲合著的经典教材，详细介绍了离散数学的各个关键部分，包括集合论、逻辑与命题、函数与关系、图论、组合数学、代数结构和形式语言与自动机。通过对这些模块的学习，学生可以培养逻辑思维、抽象思维和问题解决能力，为计算机科学深入学习奠定基础。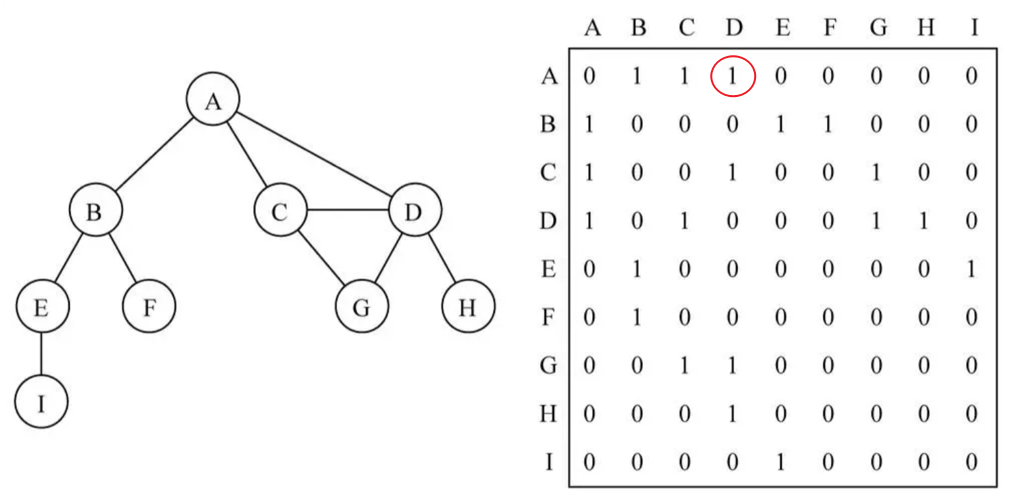

1. 集合论基础

集合论，作为数学中的一个重要分支，提供了一个强有力的工具来描述和分析离散结构。在这一章节中，我们将从集合的基础概念开始探索。

1.1 集合的基本概念

集合可以被定义为一组明确无重复的元素的全体。我们使用大写字母如A、B、C来表示集合，而使用小写字母如a、b、c来表示集合中的元素。例如，A = {1, 2, 3} 是一个包含三个元素的集合。集合之间的关系，如包含、相等、并集和交集，是理解和使用集合的基础。

1.2 集合间的基本运算

集合的基本运算包括并集、交集、差集和补集等。例如： - 并集（∪）：两个集合合并起来得到的新集合，包含所有属于这两个集合的元素。 - 例子：A ∪ B = {1, 2, 3, 4, 5}，如果 A = {1, 2, 3}，B = {3, 4, 5}。 - 交集（∩）：两个集合共有的元素构成的集合。 - 例子：A ∩ B = {3}，如果 A = {1, 2, 3}，B = {3, 4, 5}。

1.3 集合的应用实例

在计算机科学和相关领域中，集合概念有广泛的应用。例如，数据库系统中使用集合来表示表与表之间的关系，编程语言中的数据类型抽象往往利用集合论的概念。通过理解集合及其运算，可以更有效地解决复杂问题，如优化查询效率，提高数据处理的精确性。

通过本章内容的学习，读者应当能够熟练运用集合论的基本概念和运算方法，并理解其在实际应用中的重要性。

2. 逻辑与命题推理规则

2.1 命题逻辑基础

在本章中，我们将深入了解命题逻辑的基础知识，探讨命题逻辑的基本概念和命题逻辑表达式。命题逻辑是逻辑推理的基础，它涉及陈述句（命题）的真假值，以及这些命题通过逻辑运算符构建的复合表达式。每个命题在逻辑上都有一个明确的真值，即为真（T）或为假（F）。逻辑运算符包括合取（AND）、析取（OR）、否定（NOT）、蕴含（IF...THEN...）、等价（IFF...THEN...）等，它们用于构造更复杂的逻辑表达式。

2.2 逻辑运算符的含义和使用

2.2.1 合取（AND）运算符

合取运算符表示两个命题同时为真的情况。在逻辑表达式中，我们用符号 ∧ 来表示AND运算符。例如，如果命题P为真，命题Q为真，则P ∧ Q为真。

2.2.2 析取（OR）运算符

析取运算符表示两个命题至少有一个为真的情况。在逻辑表达式中，我们用符号 ∨ 来表示OR运算符。例如，如果命题P为真，命题Q为假，则P ∨ Q为真。

2.2.3 否定（NOT）运算符

否定运算符用于表示一个命题的相反真值。在逻辑表达式中，我们用符号 ¬ 来表示NOT运算符。例如，如果命题P为真，则 ¬P 为假。

2.2.4 蕴含（IF...THEN...）运算符

蕴含运算符用于表示一个命题导致另一个命题为真的关系。在逻辑表达式中，我们用符号 → 来表示蕴含。例如，如果命题P为真，命题Q为真，则P → Q为真。如果P为假，则P → Q不论Q的真值如何都为真。

2.2.5 等价（IFF...THEN...）运算符

等价运算符用于表示两个命题具有相同的真值。在逻辑表达式中，我们用符号 ↔ 或 ⇔ 来表示等价。例如，P ↔ Q 表示P和Q要么同时为真，要么同时为假。

2.3 逻辑推理规则

逻辑推理是利用命题和逻辑运算符构建逻辑论证，以推导出新结论的过程。推理的正确性依赖于推理规则的正确应用。本小节将介绍一些常用的逻辑推理规则。

2.3.1 模态推理

模态推理是基于命题真假可能性的一种推理。模态命题可以是必然（必然真或必然假）或者可能（可能真或可能假）。

2.3.2 归谬法（Reductio ad absurdum）

归谬法，即反证法，是一种通过假设某个命题为真来推导出矛盾，从而证明该命题实际上为假的逻辑推理方法。

2.3.3 条件推理

条件推理涉及条件语句（蕴含式）的推导。例如，若P → Q和P都为真，则可以推导出Q也为真。

2.4 逻辑规则的应用

2.4.1 证明逻辑表达式的有效性

证明一个逻辑表达式是否为有效式，意味着无论命题变量取什么真值，该表达式总是为真。可以通过构建真值表来验证。

graph TD
    A[构建真值表] --> B[计算逻辑表达式的真值]
    B --> C[验证所有情况下的真值]
    C --> |表达式为真| D[证明有效]
    C --> |表达式为假| E[证明无效]

2.4.2 使用逻辑推理解决数学问题

逻辑推理在数学证明中扮演着核心角色。在解题过程中，我们通常需要建立命题之间的逻辑联系，通过已知的逻辑运算结果推导出未知的结果。

graph LR
    A[提出假设] --> B[推理与计算]
    B --> C[得出结论]
    C --> |与已知结论一致| D[证明成功]
    C --> |与已知结论不一致| E[查找错误并修正]

2.4.3 解释逻辑表达式

在理解和解释逻辑表达式时，我们需要将复杂的逻辑表达式拆解为基本的命题和逻辑运算符，然后分析这些基本单元如何相互作用。

2.5 命题逻辑的应用实例

2.5.1 谜题和逻辑游戏

逻辑谜题和游戏，如数独、推箱子和逻辑游戏等，往往需要玩家运用逻辑规则进行推理，找到游戏的解决路径。

2.5.2 计算机科学中的应用

在计算机科学领域，命题逻辑被广泛应用于电路设计、程序验证、算法分析和人工智能决策过程中。

2.5.3 法律推理

在法律领域，命题逻辑可用于分析和解释法律条款，以及构建案件推理的逻辑结构。

2.6 命题逻辑练习题

通过一系列的练习题，可以帮助读者巩固对命题逻辑的理解和应用。以下是一个练习示例：

2.6.1 练习题

假设有以下命题：

P: 今天是周一 Q: 明天是周二 R: 天气晴朗

根据这些命题，构建以下逻辑表达式：

1. 如果今天是周一，那么明天是周二。
2. 如果明天是周二，那么天气晴朗。
3. 今天是周一且天气晴朗。
4. 今天不是周一或天气不晴朗。

解答：
1. P → Q
2. Q → R
3. P ∧ R
4. ¬P ∨ ¬R

通过解答这些练习题，可以帮助读者深入理解逻辑表达式构建和逻辑推理的过程。

3. 函数与关系的性质

函数与关系是描述数学对象间相互作用与联系的基础工具。它们不仅在数学领域内拥有广泛应用，也是计算机科学、数据分析、物理学等多个学科不可或缺的组成部分。本章内容将从基础开始，逐步深入探讨函数与关系的定义、性质和重要应用。通过本章节的深入研究，读者将能更好地理解这些基础概念，并能够将它们应用于实际问题的求解中。

3.1 函数与关系的基本概念

3.1.1 函数的定义与表示

在数学中，函数可以被视为一种特殊的对应关系，它将一个集合中的每一个元素映射到另一个集合中的唯一元素。这种对应关系是函数的核心特性，即每一个输入值（定义域中的元素）都有唯一的输出值（值域中的元素）与之对应。

例如，考虑函数 f(x) = x + 2 ，这个函数将任意实数映射到比它大的另一个实数，即输入值 x 映射到输出值 x + 2 。

3.1.2 关系的定义与分类

关系是指任意两个集合间元素的联系。如果集合 A 中的每一个元素都与集合 B 中的至少一个元素有联系，则称 A 与 B 之间存在关系。关系可以是函数关系，也可以是非函数关系。

关系可以根据其特性被分类为自反的、对称的、传递的等，这些特性定义了关系的不同类型。

3.2 函数与关系的性质

3.2.1 函数的性质

函数的主要性质包括：

• 单射（Injective） ：如果不同的元素在函数的作用下映射到不同的结果，则称此函数为单射。
• 满射（Surjective） ：如果函数的值域等于其到达集合，则称此函数为满射。
• 双射（Bijective） ：同时满足单射和满射条件的函数称为双射。双射函数可以保证一一对应关系。

3.2.2 关系的性质

关系的性质通常包括：

• 自反性 ：一个关系是自反的，如果对于集合中的每一个元素，它都与自己有关联。
• 对称性 ：一个关系是对称的，如果当元素 A 与元素 B 有关系时，元素 B 与元素 A 也有关系。
• 传递性 ：一个关系是传递的，如果当元素 A 与元素 B 有关系，且元素 B 与元素 C 有关系时，元素 A 与元素 C 也有关系。

3.3 函数与关系的应用

3.3.1 函数的应用实例

函数广泛应用于物理学中的速度与时间关系，经济学中的供需模型，以及计算机科学中的算法复杂性分析等领域。

例如，在经济学中，供给函数 Q = f(P) 可以描述产品数量 Q 与价格 P 之间的关系。

3.3.2 关系的应用实例

关系在数据库理论中尤为重要，它们用于定义实体间的关系，例如一对多、多对多等。

在社交网络中，关系可以被用来表示用户之间的连接，如“朋友”关系。

3.4 复合函数和逆函数的相关性质

3.4.1 复合函数的定义与性质

复合函数是由两个或更多的函数组合而成的新函数。如果函数 f 的输出值作为函数 g 的输入值，则复合函数可以写作 g(f(x)) 。复合函数的性质包括：

• 结合律 ： (g ∘ f) ∘ h = g ∘ (f ∘ h) 对于函数的复合操作成立。
• 存在性 ：如果 f 的值域与 g 的定义域有交集，则复合函数 g ∘ f 存在。

3.4.2 逆函数的定义与性质

逆函数是指将函数的作用逆转的函数。如果函数 f 将 x 映射到 y ，即 y = f(x) ，那么存在一个逆函数 f⁻¹ 将 y 映射回 x ，即 x = f⁻¹(y) 。逆函数的性质包括：

• 唯一性 ：对于给定的函数 f ，其逆函数 f⁻¹ 是唯一的，如果存在。
• 运算性 ： (f⁻¹ ∘ f) 和 (f ∘ f⁻¹) 都等于定义域和值域上的恒等函数。

3.4.3 复合函数与逆函数的应用

复合函数和逆函数在解决实际问题中非常有用。例如，在加密学中，复合函数可以用来设计复杂的加密算法，而逆函数则用于解密过程。

在计算机图形学中，复合函数可以用于变换物体的位置和方向，而逆函数则用于将变换的过程逆转，实现撤销操作。

3.5 函数与关系的可视化表示

函数与关系的可视化有助于直观理解它们的性质和行为。通过绘制图像和创建表格，我们可以更清晰地展示函数与关系之间的联系。

3.5.1 函数的图像表示

函数的图像通常是一条曲线，可以通过绘图工具或计算机软件绘制。

例如，函数 f(x) = x^2 的图像是一条对称的抛物线，它可以告诉我们关于函数的很多性质，如增减性、极值点等。

3.5.2 关系的图表示法

关系可以用图来表示，其中集合的元素用节点表示，元素间的关系用有向边或无向边表示。

例如，可以用图来表示社交网络中用户的关系，其中节点表示用户，边表示用户之间的朋友关系。

3.6 函数与关系的实际操作案例

3.6.1 利用函数进行数据分析

函数在数据分析中有着广泛应用，如使用函数模型来预测未来的趋势，或者通过函数来拟合实际的数据点。

3.6.2 关系数据库中查询优化

在关系数据库中，关系用于定义表之间的连接。查询优化依赖于对关系的理解，通过减少不必要的连接操作或合理利用索引，可以显著提高查询效率。

3.6.3 应用函数解决实际问题

函数在实际问题中有着广泛的应用。例如，在城市规划中，可以使用函数来模拟交通流量和预测拥堵情况，从而为交通管理提供决策支持。

通过本章的深入讨论，我们不仅学习了函数与关系的基础概念和性质，而且探索了它们在实际应用中的价值。函数与关系是连接数学与现实世界的重要桥梁，理解并能够运用它们，对于从事相关领域工作的人来说至关重要。

4. 图论概念与遍历算法

图论是离散数学中的一个核心分支，它不仅在数学领域具有广泛的应用，而且在计算机科学、工程学、社会科学等诸多领域都发挥着重要的作用。图由顶点（节点）和连接这些顶点的边组成，可以用来表示各种复杂的关系网络。本章将深入介绍图论的基本概念、图的分类以及图的遍历算法，这些内容对于理解后续章节中介绍的网络算法和优化问题至关重要。

图的基本概念与分类

在图论中，我们通常将图定义为 G = (V, E)，其中 V 表示顶点集合，E 表示边集合。边可以是有向的，也可以是无向的。有向边表示从一个顶点指向另一个顶点的方向，无向边则表示两个顶点之间是双向连接的。

有向图和无向图

• 有向图（Directed Graph） ：图中的每条边都是有方向的，通常用一对有序顶点来表示，例如 (u, v) 表示一条从顶点 u 指向顶点 v 的有向边。
• 无向图（Undirected Graph） ：图中的每条边都是无方向的，连接两个顶点但不指明方向，通常用一对无序顶点来表示，例如 {u, v} 表示顶点 u 和顶点 v 之间有一条连接。

完全图、稀疏图与密集图

• 完全图（Complete Graph） ：图中任意两个不同的顶点之间都存在一条边。在有向完全图中，每一对顶点之间都存在两条有向边，一条指向对方。
• 稀疏图（Sparse Graph） ：边的数量远少于可能的最大边数，即顶点总数的平方。
• 密集图（Dense Graph） ：边的数量接近可能的最大边数，即顶点总数的平方减去顶点总数，因为不能有自环（即边的起点和终点是同一个顶点）。

带权图和无权图

• 带权图（Weighted Graph） ：边有权重，表示连接两个顶点的边具有特定的数值属性，比如距离、成本或容量等。
• 无权图（Unweighted Graph） ：边没有权重，所有边都被认为是等价的。

示例代码

下面是一个简单的Python代码示例，展示了如何用邻接矩阵表示有向图和无向图，并进行初始化。

class Graph:
    def __init__(self, vertices, graph_type='undirected'):
        self.V = vertices  # Number of vertices in the graph
        self.graph_type = graph_type
        self.graph = [[0] * vertices for _ in range(vertices)]  # Initialize matrix

    def add_edge(self, u, v):
        if self.graph_type == 'undirected':
            self.graph[u][v] = 1
            self.graph[v][u] = 1  # Since it is undirected
        else:
            self.graph[u][v] = 1  # For directed graph

    def print_graph(self):
        for row in self.graph:
            print(row)

# 创建无向图实例
undirected_graph = Graph(4)
undirected_graph.add_edge(0, 1)
undirected_graph.add_edge(0, 2)
undirected_graph.add_edge(1, 2)
undirected_graph.add_edge(2, 3)
undirected_graph.print_graph()

# 创建有向图实例
directed_graph = Graph(4, graph_type='directed')
directed_graph.add_edge(0, 1)
directed_graph.add_edge(1, 2)
directed_graph.add_edge(2, 3)
directed_graph.print_graph()

在上述代码中，我们定义了一个 Graph 类，它可以创建有向图和无向图。通过使用邻接矩阵来初始化图，并添加边。 print_graph 方法用来打印邻接矩阵，从而可视化图的结构。

图的表示方法

• 邻接矩阵（Adjacency Matrix） ：用一个二维数组来表示图，其中的元素表示顶点之间的连接关系。对于带权图，元素值是边的权重；对于无权图，元素值通常为1或0。
• 邻接表（Adjacency List） ：使用一个数组来存储每个顶点的邻接点。数组的每个元素是一个列表，列表中的每个元素是与该顶点直接相连的顶点。

在下一节中，我们将探讨如何遍历图中的所有顶点，并介绍深度优先搜索（DFS）和广度优先搜索（BFS）这两种经典的图遍历算法。

图的遍历算法

图的遍历算法主要有深度优先搜索（DFS）和广度优先搜索（BFS）。它们是图算法中最基础也是最常见的算法，用于搜索图中的顶点或边。在实际应用中，DFS和BFS常用于解决路径问题、最短路径问题以及网络爬虫等。

深度优先搜索（DFS）

深度优先搜索（Depth-First Search, DFS）是一种用于遍历或搜索树或图的算法。该算法沿着图的边尽可能深地搜索路径，直到到达一个节点，该节点没有任何未被访问过的邻接节点，然后回溯。

DFS算法步骤

1. 从图的根节点开始。
2. 访问节点并将其标记为已访问。
3. 对于该节点的所有未访问的邻接节点，递归地进行深度优先搜索。

DFS伪代码

DFS(graph, vertex, visited):
    if vertex is visited:
        return
    mark vertex as visited
    process vertex
    for each neighbor in graph.adjacent(vertex):
        if neighbor is not visited:
            DFS(graph, neighbor, visited)

广度优先搜索（BFS）

广度优先搜索（Breadth-First Search, BFS）是一种用于遍历或搜索树或图的算法。该算法从根节点开始，先访问所有邻近节点，然后再访问邻近节点的邻近节点，以此类推。

BFS算法步骤

1. 创建一个队列 Q，并将起始节点压入队列。
2. 若队列非空，将队首节点弹出，并标记为已访问。
3. 将该节点的所有未访问的邻接节点压入队列。
4. 重复步骤2和3，直到队列为空。

BFS伪代码

BFS(graph, start):
    create a queue Q
    enqueue start to Q
    mark start as visited
    while Q is not empty:
        vertex = Q.dequeue()
        process vertex
        for each neighbor in graph.adjacent(vertex):
            if neighbor is not visited:
                mark neighbor as visited
                Q.enqueue(neighbor)

示例代码

以下是使用Python实现DFS和BFS算法的代码示例。

from collections import deque

# DFS 递归实现
def dfs_recursive(graph, vertex, visited=None):
    if visited is None:
        visited = set()
    visited.add(vertex)
    print(vertex)
    for neighbor in graph[vertex]:
        if neighbor not in visited:
            dfs_recursive(graph, neighbor, visited)
    return visited

# BFS 迭代实现
def bfs_iterative(graph, start):
    visited = set()
    queue = deque([start])
    while queue:
        vertex = queue.popleft()
        if vertex not in visited:
            print(vertex)
            visited.add(vertex)
            queue.extend(set(graph[vertex]) - visited)
    return visited

# 构建图的邻接表表示
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

# 执行DFS和BFS
dfs_recursive(graph, 'A')
print("\n BFS Traversal:")
bfs_iterative(graph, 'A')

在上述代码中，我们使用字典来表示图的邻接表。 dfs_recursive 函数实现了DFS算法的递归版本，而 bfs_iterative 函数则实现了BFS算法的迭代版本。两者都能够遍历图中的所有节点，并在控制台上打印访问顺序。

通过DFS和BFS的实现，我们可以观察到两种算法的搜索路径和方式有所不同。DFS倾向于尽可能深地遍历图的分支，而BFS则会从起始点开始按层次逐渐向外扩展。

算法分析

DFS和BFS的时间复杂度都是O(V+E)，其中V表示顶点数，E表示边数。空间复杂度主要取决于图的表示和递归调用栈，对于BFS来说，空间复杂度为O(V)。

应用场景

• DFS ：常用于路径寻找、拓扑排序、检测图的连通分量以及解决棋盘问题等。
• BFS ：用于找出最短路径，比如在社交网络中寻找两个人之间的最短联系路径。

结论

通过本节的学习，我们了解了图的定义、分类以及图的两种基本遍历算法——DFS和BFS。在实际应用中，根据不同的需求选择合适的遍历算法至关重要。在下一节中，我们将继续探索图论的高级概念，如连通性、强弱连通分量等，以及更高级的图算法。

5. 组合数学原理

5.1 排列组合的基本原则

排列和组合是组合数学中最基本的概念，它们在解决计数问题中扮演着重要的角色。具体来说，排列关注的是元素的顺序，而组合则不考虑元素的顺序。

5.1.1 排列的概念及其计算

排列是指从n个不同元素中取出m（m≤n）个元素的所有可能方式的数目。排列的数目可以通过排列公式计算得出：

[ P(n, m) = \frac{n!}{(n-m)!} ]

这里 n! 表示n的阶乘，即从1乘到n的乘积。例如，从5个不同的元素中取出3个元素的排列数为：

[ P(5, 3) = \frac{5!}{(5-3)!} = \frac{120}{2} = 60 ]

5.1.2 组合的概念及其计算

与排列不同，组合关注的是选择的元素本身而不是它们的顺序。组合的数目可以通过组合公式计算得出：

[ C(n, m) = \frac{P(n, m)}{m!} = \frac{n!}{m!(n-m)!} ]

例如，从5个不同的元素中取出3个元素的组合数为：

[ C(5, 3) = \frac{5!}{3!2!} = \frac{120}{6} = 20 ]

5.1.3 排列与组合的实例应用

在现实世界中，排列和组合的概念有很多应用。比如在密码学中，确定密码的组合数，或者在游戏设计中，计算玩家获胜的概率。

5.1.4 排列组合的代码实现

在Python中，可以使用内置函数或者自定义函数来计算排列和组合的数目：

import math

def permutation(n, m):
    return math.factorial(n) // math.factorial(n - m)

def combination(n, m):
    return math.factorial(n) // (math.factorial(m) * math.factorial(n - m))

# 使用函数
n, m = 5, 3
print(f"排列数 P({n}, {m}) = {permutation(n, m)}")
print(f"组合数 C({n}, {m}) = {combination(n, m)}")

5.1.5 排列组合的逻辑分析

在代码中，首先导入了 math 模块来使用阶乘函数。 permutation 函数计算排列数，而 combination 函数计算组合数。通过数学上的阶乘定义，我们可以得出排列和组合的计算公式。接着，我们用具体的数字n和m来调用这些函数，并打印结果。

5.2 二项式定理及其应用

二项式定理是组合数学中的一个重要定理，它提供了二项式（a+b）的幂展开的通项公式。

5.2.1 二项式定理介绍

二项式定理可以表示为：

[ (a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k ]

其中，(\binom{n}{k})表示二项式系数，可以通过(\frac{n!}{k!(n-k)!})来计算。

5.2.2 二项式系数的计算

使用二项式系数可以简化很多计数问题的计算。比如，在掷骰子问题中，求掷出特定点数的组合方式数目。

5.2.3 二项式定理在概率论中的应用

二项式定理在概率论中有着广泛的应用，特别是在二项分布中。二项分布的概率质量函数可以通过二项式定理来推导。

5.2.4 二项式定理的代码实现

在Python中，我们可以使用 math 模块来计算二项式系数，并用它来展开二项式：

import math

def binomial_coefficient(n, k):
    ***b(n, k)

def expand_binomial(a, b, n):
    result = 0
    for k in range(n + 1):
        result += binomial_coefficient(n, k) * (a**(n - k) * b**k)
    return result

# 使用函数
a, b, n = 2, 3, 5
print(f"二项式系数 C({n}, 3) = {binomial_coefficient(n, 3)}")
print(f"二项式展开 (a + b)^{n} = {expand_binomial(a, b, n)}")

5.2.5 二项式定理的逻辑分析

在上述代码中， binomial_coefficient 函数用于计算二项式系数，它使用了Python 3.8引入的 ***b 函数。 expand_binomial 函数用于展开二项式，它通过遍历k从0到n的所有可能值，并根据二项式系数计算每一项的值，最后将它们累加起来得到展开后的结果。

5.3 组合方法解决实际问题

组合数学不仅仅是理论知识，它还能解决很多实际问题，比如在资源分配、计划调度等方面。

5.3.1 资源分配问题的组合解法

在资源分配问题中，我们要考虑的是如何将有限资源分配给需求者，组合数学可以帮助我们计算出最优的分配方案。

5.3.2 计划调度问题的组合优化

在计划调度问题中，我们可以使用组合数学的方法来找出最有效的任务执行顺序，以减少资源的浪费。

5.3.3 组合方法的代码实现

假设我们要解决一个简单的资源分配问题，我们可以编写一个程序来模拟资源的分配过程：

from itertools import permutations

def resource_allocation(resources, demanders):
    # 生成需求者的排列，作为分配方案
    allocations = list(permutations(resources, len(demanders)))
    return allocations

# 使用函数
resources = ['A', 'B', 'C']
demanders = [1, 2, 3]
allocations = resource_allocation(resources, demanders)
for i, allocation in enumerate(allocations):
    print(f"方案 {i + 1}: {allocation}")

5.3.4 组合方法的逻辑分析

在上述代码中，我们使用了 itertools.permutations 来生成所有可能的资源分配方案。这里的资源分配问题通过简单的排列来模拟，可以看作是一个资源到需求者的一一映射。通过遍历所有排列，我们可以找到所有可能的资源分配方案，并进行分析和选择。

5.4 组合数学与其他数学分支的关联

组合数学不仅独立应用广泛，还与其他数学分支有着紧密的联系，比如它与线性代数、概率论、统计学等多个领域都有交集。

5.4.1 组合数学与线性代数的联系

在某些问题中，组合结构可以用向量和矩阵来表示，从而应用线性代数的方法进行分析和计算。

5.4.2 组合数学在概率论中的作用

组合数学在概率论中发挥着基础性作用，尤其是在计算概率时，经常需要用到排列和组合的知识。

5.4.3 组合数学与统计学的相互影响

在统计学中，组合数学可以帮助我们理解数据的组合模式，从而更好地进行数据分析和推断。

5.4.4 组合数学在其他领域的影响

组合数学的方法也被广泛应用在计算机科学、运筹学、生物信息学等领域，为解决复杂问题提供了工具。

通过本章内容的介绍，我们可以看到组合数学在计数问题、资源分配、计划调度等实际问题中发挥的重要作用。它不仅帮助我们理解世界，还为我们提供了用于解决问题的多种组合方法。

6. 代数结构概述

代数结构在数学中是一类拥有特定运算规则的集合，它们构成了现代数学的基石之一，并广泛应用于物理、计算机科学、密码学等领域。本章内容将着重于群、环、域的基本概念和性质，这些结构构成了代数系统的主要框架，并通过实例展示这些代数结构在各个领域的实际应用。

6.1 群的基本概念

群的定义与性质

群是代数结构中最基本的类型，它是由一组元素以及在这些元素上定义的一个二元运算构成，满足四个基本条件：封闭性、结合律、单位元的存在和每个元素有逆元。在实际应用中，群经常用于表示对称性，例如几何图形的对称操作、多项式的根的排列等。

群的定义

群（G, ）由非空集合 G 和运算 * 组成，满足以下条件： 1. 封闭性 ：对于任意 a, b ∈ G，有 a * b ∈ G。 2. 结合律 ：对于任意 a, b, c ∈ G，有 (a * b) * c = a * (b * c)。 3. 单位元 ：存在元素 e ∈ G，使得对任意 a ∈ G，有 e * a = a * e = a。 4. 逆元 *：对于任意 a ∈ G，存在元素 b ∈ G 使得 a * b = b * a = e。

群的类型

群可以分为多种类型，例如交换群（或阿贝尔群），其运算满足交换律；有限群和无限群，分别表示群的元素数量是有限或无限的；还有循环群，它的任何元素都可以由群中的一个元素通过重复运算生成。

群在现代数学中的应用

群的理论在现代数学中有着广泛的应用，例如在拓扑学中，基本群用于描述空间的“洞”的结构；在数论中，模算术形成了一个群；在物理学中，李群用于描述对称性和守恒定律。

6.2 环和域的基本概念

环的定义与性质

环是另一种重要的代数结构，它由一组元素和两个二元运算（通常是加法和乘法）组成，并满足加法的群结构以及乘法的封闭性和结合律，并且加法和乘法之间满足分配律。

环的定义

环（R, +, *）由非空集合 R 和两个运算 + 和 * 组成，满足以下条件： 1. （R, +）是一个加法交换群。 2. 对于任意 a, b, c ∈ R，有 (a * b) * c = a * (b * c)。 3. 对于任意 a, b ∈ R，有 a * b = b * a（乘法交换律，不一定是环的所有类型都满足）。 4. 对于任意 a, b, c ∈ R，有 a * (b + c) = (a * b) + (a * c)（左分配律）和 (b + c) * a = (b * a) + (c * a)（右分配律）。

域的定义与性质

域是一种特殊类型的环，在其中每个非零元素都有逆元。这意味着在域中可以执行除法运算（除了除以零）。

域的定义

域（F, +, ）由非空集合 F 和两个运算 + 和 * 组成，其中（F, +）是一个加法交换群，（F-{0}, ）是一个乘法交换群，且满足加法和乘法的分配律。

环和域在现代数学和相关领域的应用

环和域的理论在数学分析、代数几何、密码学等领域都有重要应用。例如，在编码理论中，域的概念用于构造和分析线性码；在代数几何中，环的理论用于定义代数簇。

6.3 代数结构的应用实例

实例一：密码学中的群论应用

群论在密码学中的一个应用是素数阶循环群的生成，这是基于椭圆曲线密码学的基础。椭圆曲线上的点可以形成一个有限群，其中的运算满足群的定义，而这些性质被用来构造密钥对和执行加密。

实例二：整数模运算形成的环

整数模 n 形成一个环，这是密码学中广泛应用的模算术的基础。模算术是构建散列函数和块加密算法（如AES）的关键工具。

实例三：数域在密码学中的应用

数域是域的一个实例，它在密码学中用于有限域或伽罗瓦域，这为公钥加密提供了代数基础。例如，利用有限域上的多变量多项式方程构造的加密系统，被用于防止特定类型的数学攻击。

实例四：代数结构在计算机图形学中的应用

在计算机图形学中，群论可以用来模拟和分析几何变换，如旋转、缩放和平移等。这些变换常常构成群，为图形变换提供了代数框架。

实例五：代数结构在量子计算中的应用

量子计算中，量子位的操作遵循某些群的规则。例如，量子比特的旋转操作构成一个群，这些操作反映了量子力学的对称性，并且是量子算法的基础。

6.4 代数结构的编程应用

6.4.1 群论与编程

在计算机科学中，群的概念可以用于算法设计和软件工程。例如，一个类的设计可以遵循群的结构，以确保操作的正确性和一致性。

代码块示例与分析

class SymmetryGroup:
    def __init__(self, elements):
        self.elements = elements

    def operate(self, a, b):
        """定义群的运算"""
        # 实际应用中需要根据具体的群性质来定义这个运算
        pass

    def inverse(self, a):
        """返回元素a的逆元"""
        # 实际应用中需要根据具体的群性质来定义这个逆运算
        pass

# 创建一个群实例
g = SymmetryGroup(elements=[...])

# 执行群运算
a = g.elements[0]
b = g.elements[1]
result = g.operate(a, b)

# 找到元素的逆元
inverse_a = g.inverse(a)

在上述代码中，我们定义了一个群的抽象类 SymmetryGroup ，它包含了元素集合和运算方法，以及寻找元素逆元的方法。在具体实现时，需要根据实际的群结构来定义运算和逆运算。

6.4.2 环和域在编程中的表示

在编程中，我们可以定义环和域的结构来模拟数学中的概念。例如，我们可以创建一个域的类，该类包含了所有域必须满足的运算规则。

代码块示例与分析

class Field:
    def __init__(self, elements):
        self.elements = elements

    def add(self, a, b):
        """定义加法运算"""
        pass

    def multiply(self, a, b):
        """定义乘法运算"""
        pass

    def add_inverse(self, a):
        """返回元素a的加法逆元"""
        pass

    def multiply_inverse(self, a):
        """返回元素a的乘法逆元（除了0之外）"""
        pass

# 创建一个域实例
f = Field(elements=[...])

# 执行域运算
a = f.elements[0]
b = f.elements[1]
sum_result = f.add(a, b)
product_result = f.multiply(a, b)

在这个 Field 类中，我们定义了加法和乘法运算，以及它们的逆运算，来保证域的结构。在实例化时，我们需要提供具体的元素集合，并实现运算方法，以确保它们满足域的所有性质。

6.5 本章总结

在本章中，我们介绍了代数结构的基本概念，包括群、环和域，以及它们的性质和类型。我们探讨了代数结构在现代数学和相关领域中的应用，特别是在密码学、计算机图形学和量子计算中的重要性。通过具体的实例，展示了如何在实践中使用这些概念。最后，我们通过编程实例展示了如何在编程中实现和操作代数结构，强调了理论与实践相结合的重要性。

以上内容展示了第六章“代数结构概述”的结构和内容，按照要求从浅入深地逐步引导读者理解这一重要数学分支，并通过实例将理论与现代科技应用联系起来，最后提供了代码示例，帮助读者通过编程实现相关概念。

7. 形式语言与自动机基础

形式语言和自动机理论是计算机科学的基石，它们在理解计算机程序设计语言和人工智能中扮演着至关重要的角色。本章将介绍形式语言和自动机的定义、基本概念和理论，以及它们在计算机程序设计语言中的应用。我们将从形式语言的构成开始，逐步深入到自动机的理论和实践。

7.1 形式语言和文法的基本概念

在正式探讨自动机之前，我们需要了解形式语言的基础知识。形式语言是一组有限或无限字符串的集合，这些字符串由有限的字母表（符号集）构成。而文法则是定义形式语言结构的一组规则。

7.1.1 字母表与字符串

• 字母表 ：形式语言由一个有限的字符集构成，这个集合称为字母表。
• 字符串 ：字母表中的字符按照一定顺序排列成的有限序列称为字符串。

7.1.2 形式语言的定义

• 语言 ：由特定字母表生成的所有可能字符串的集合称为形式语言。
• 递归定义 ：形式语言可以通过递归的方式定义，即从一组初始字符串（称为句子）开始，通过应用生成规则（文法规则）来产生新的字符串。

7.1.3 文法的分类

• 0型文法（无限制文法） ：每个文法规则的左边是一个符号，右边是任意长度的符号序列。
• 1型文法（上下文相关文法） ：规则左边的符号必须被上下文符号包围。
• 2型文法（上下文无关文法） ：规则左边仅有一个符号。
• 3型文法（正规文法） ：规则分为两种类型：要么是将一个符号替换为另一个符号，要么是在字符串的开始或结束位置添加一个符号。

7.2 有限自动机和下推自动机

自动机是计算机科学中用于识别和处理特定输入序列的抽象计算模型。有限自动机（FA）和下推自动机（PDA）是其中的两种基本类型。

7.2.1 有限自动机（FA）

• 定义 ：有限自动机是一种模型，由一组状态、一个初始状态、一组接受状态和转移函数组成。
• 状态转移 ：FA根据当前状态和输入符号，通过转移函数转移到下一个状态。

7.2.2 下推自动机（PDA）

• 定义 ：下推自动机是带有额外的栈数据结构的自动机，除了FA的所有组件外，它还有栈操作（压栈和弹栈）。
• 使用栈的优势 ：PDA能够处理那些有限自动机无法处理的上下文相关语言。

7.2.3 自动机的作用

• 识别语言 ：FA和PDA可以被用来识别特定形式的语言。
• 实现编译器 ：编译器的词法分析器通常使用FA来识别源代码中的符号，而语法分析器往往使用PDA来构建语法树。

7.3 自动机在程序设计语言中的应用

形式语言和自动机的理论在程序设计语言的编译过程中扮演着核心角色。在编译器的不同阶段，FA和PDA被用来处理源代码，确保其符合特定的语法规则。

7.3.1 词法分析

• 任务 ：词法分析器将源代码文本分解成一系列标记（tokens）。
• 实现 ：使用FA可以识别诸如标识符、关键字、运算符等标记。

7.3.2 语法分析

• 任务 ：语法分析器检查标记序列是否符合程序设计语言的语法规则。
• 实现 ：PDA在这里发挥重要作用，帮助构建一个符合语法规则的结构化表示（如抽象语法树）。

7.3.3 代码生成和优化

• 代码生成 ：将抽象语法树转换为机器代码。
• 代码优化 ：自动机理论也可用于代码优化，提高程序的性能。

7.3.4 实例：简单编译器的构造

为了说明FA和PDA在实际中的应用，我们可以构造一个简单的编译器框架。这个框架会展示如何使用FA进行词法分析，以及如何使用PDA进行语法分析。

代码块是一个简化的例子，描述了使用有限自动机进行词法分析的过程：

# Python 伪代码，使用正则表达式来模拟 FA 的词法分析过程
import re

# 示例：一个简单的词法分析器，用于识别整数和操作符
lexer_rules = {
    'INTEGER': r'\d+',  # 匹配整数
    'PLUS': r'\+',     # 加号
    'MINUS': r'-',     # 减号
}

# 文本输入
source_code = "123 + 45 - 6"

# 识别所有标记
tokens = [(token, re.search(pattern, source_code)) for token, pattern in lexer_rules.items()]

# 提取标记的值
tokens = [(token, match.group(0)) for token, match in tokens if match]

print(tokens) # 输出识别到的标记

通过上述的编译器框架，我们可以看到FA和PDA的理论如何实际应用于程序语言的处理过程中。最终，形式语言和自动机的深入理解将为设计更高效的编译器和程序提供坚实的基础。

本文还有配套的精品资源，点击获取

简介：离散数学是计算机科学的基础课程，它涉及算法设计、数据结构、逻辑推理等多个核心领域。本课件基于耿素云和屈婉玲合著的经典教材，详细介绍了离散数学的各个关键部分，包括集合论、逻辑与命题、函数与关系、图论、组合数学、代数结构和形式语言与自动机。通过对这些模块的学习，学生可以培养逻辑思维、抽象思维和问题解决能力，为计算机科学深入学习奠定基础。

本文还有配套的精品资源，点击获取