归一化强度代表什么_量子态以及其归一化:量子信息的视角

本文使用 Zhihu On VSCode 创作并发布

量子态

在量子物理的视角下，量子态（quantum state)是用来描述一个系统的每种可能的结果的概率分布的数学量。与此同时，一个系统的行为可以通过量子态以及整个系统随时间的演化(evolution)方程(薛定谔方程)预测。

量子态，广义上可以分为纯态（纯量子态）和混合量子态两种。其中混合量子态的定义不是统一的，在稍后的篇幅中会指出不同点。需要注意的是，量子态使用数值描述时是定义于整个复数域的。

对于一个量子系统而言，其具有一个对应的希尔伯特空间(Hilbert Space)，也就是一种广义的完备的内积空间（可以将其视作欧几里得空间在无穷维上的扩展）。所以这个量子系统的量子态可以用其对应的希尔伯特空间的向量表示。这便被称为状态向量（state vector,在部分资料中被翻译为态矢）。由于在量子力学中，如果某个状态向量是另一个状态向量的标量倍数，那么这两个状态向量被认为对应着同样的量子态。故状态向量的L2范数并没有物理意义，只有方向才具有物理意义。

因此，为了统一起见，所有的状态向量的L2范数都被设定为1，所以一个量子系统的所有的状态向量的集合是这个系统对应的希尔伯特空间的单位球。由于状态向量的元素是复数域的，因此如果两个状态向量仅仅只有全局相位因子(global phase factor)不同，那么这两个状态向量依旧代表同一个量子态。也就是当

，且

时,可以认为这两个状态向量表示同一个量子态，因为这两个状态向量的范数也就是概率（振幅）一致。

纯态

纯态的定义

纯态(Pure State)，在一些场景中可能被称为状态向量(state vector)或者波函数(wave function)，当一个量子态能被描述为其他量子态的一种混合（mixture）的时候，这个量子态就是纯态（表示的）。如果一个量子系统具有精确的已知状态的时候，也称其处于纯态。

纯态的性质

如果将纯态写作为状态向量的形式时，纯态的态矢(系数向量)

符合L2归一。如果有：

,那么：

其中，

是指纯态

的状态向量的第

个分量的值，而

指的是这个分量的绝对值（模长）。由于这里的向量是复数域的，对于复数

而言，其模长为

。

因此可以发现，如果将纯态通过状态向量的视角表述，那么纯态是一个位于

维内积空间中的单位球上的向量，这个结果于上一小节的定义相符。特别的，在双态系统中的纯态空间几何表示方法是Bloch Sphere，布洛赫球面。

补充：纯态的表示以及Bloch Sphere

在量子力学中，数学表示可以是多样的，在这里可以先行引入密度矩阵或密度算子的概念。给定纯态

，使用状态向量这一数学表示，可以调用Dirac Notation得到：

,或者使用密度矩阵表示：

思考：结合第一部分的量子态L2范数归一的规定，为什么纯态的密度矩阵这一数学表示可以和状态向量等价。

Bloch Sphere

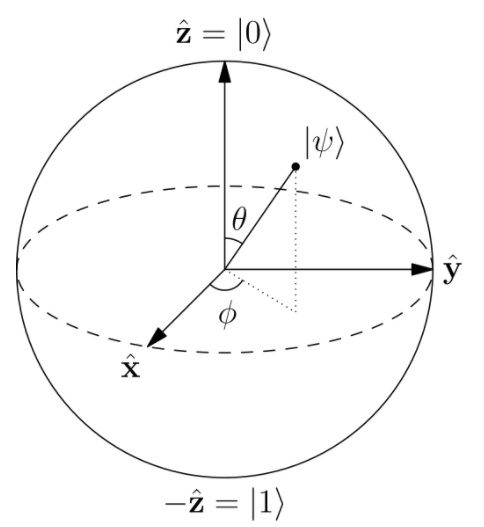
z轴的两端分别是一对本征态

和

,由于纯态的L2归一性易得：这两个本征态对应的本征值都为1，因为这个球是个单位球，球面上所有点到球心到距离均为1，因此本征态模长不变，故本征值也就是几何意义的缩放因子，也为1。

由于纯态可以用状态向量表示且满足L2归一（特别的，这里的写法体现了量子叠加，下一部分将会详细描述）

所以可以表达为：

其中

表示0和1态的相对相位因子，根据量子态小节的结论，可以发现这里并不需要写全局相位因子，而这个表达方式将原先的

和