两条平行导线同向电流_大物学习笔记（十六）——磁场对载流导线的作用与磁介质...

目录：

空山新雨后：大物学习笔记（目录）​zhuanlan.zhihu.com

---

安培力

• 公式：
  （B和L都是向量，同样满足向量叉乘）如果不是直线的话，利用微分的思想。
  • 对于任意曲线：如果磁场强度不变可以连接首尾等效代替。

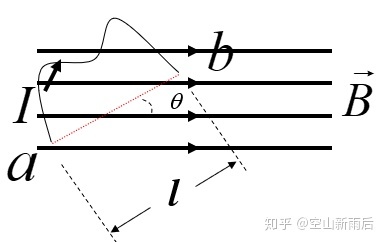
• 推导：单个电荷的受力
  。单位长度的受力就是
  。然后积分就是
  。

例题

---

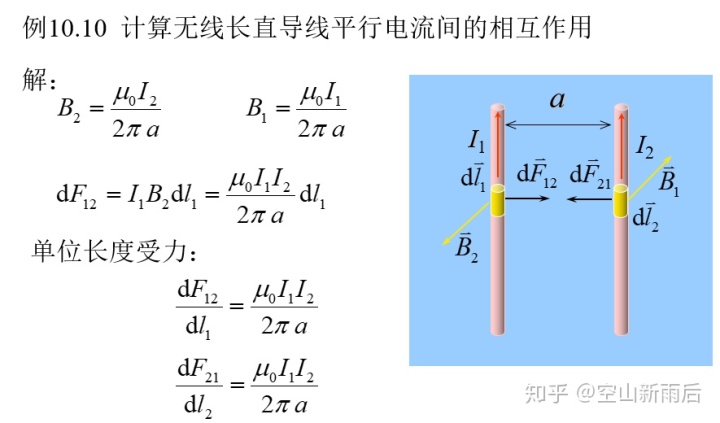
磁力矩

• 线圈的磁力矩：
  （P与B都是矢量，满足矢量叉乘）
• 线圈的磁矩：
  。（N线圈匝数，I线圈中电流，S线圈面积）
  适用于任意形状的线圈。

例题

1.有一半径为R的闭合载流线圈，通过电流I。今把它放在均匀磁场中，磁感应强度为B，其方向与线圈平面平行。求：以直径为转轴，线圈所受磁力矩的大小和方向。

解法一：利用微元的思想

以直径为转轴，那么直径上的受力肯定不产生力矩。那么圆弧上，单位长度的力矩就是

。单位长度

。

所以积分

解法二：利用公式

所以

---

磁场的功

• 载流导线在磁场中运动：
• 磁力矩的做功：
  (力矩做功参见刚体运动大物学习笔记（二）)

例题

---

磁介质

• 物质的磁化： 当一块介质放在外磁场中将会与磁场发生相互作用，产生一种所谓的“磁化”现象，介质中出现附加磁场。我们把这种在磁场作用下磁性发生变化的介质称为“磁介质”。简单来讲就是有了一个磁场，介质在此磁场的作用下，产生一个附加磁场，介质中的磁场就发生了变化。
• 磁介质中的磁场：
• 相对磁导率：
• 四种磁介质：
  • 顺磁性介质：介质磁化后呈弱磁性。附加磁场
    与外场
    同向。
    。
  • 抗磁性介质：介质磁化后呈弱磁性。附加磁场
    与外场
    反向。
    。
  • 铁磁性介质：介质磁化后呈强磁性（如电磁铁的铁芯）。附加磁场
    与外场
    同向。
    。
  • 完全抗磁体：磁介质内的磁场等于零（如超导体）。附加磁场
    与外场
    等大反向。
    。

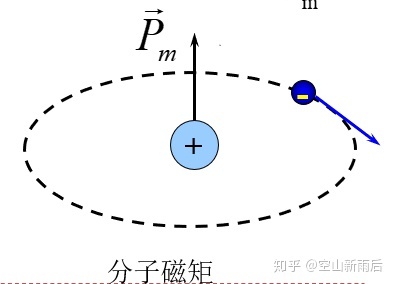
• 分子磁矩：
  。分子中各电子的轨道运动和自旋产生的磁矩之和。（计算参加磁矩）

• 磁化强度：
  。磁化强度是空间坐标的矢量函数。当磁化强度矢量为恒矢量时，磁介质被均匀磁化。
  • 单位：A/m
• 有介质存在时的高斯定理 :
  。磁介质在磁化后，由于外磁场和附加磁场都属于涡旋场。因此，在有磁介质存在时，磁场中的高斯定理仍成立。
• 有介质存在时的安培环路定理 ：
  • 满足：
    ，
    （证明过程参考电场的介质中的高斯定理）

---

（所有图片均来自网络，侵删）