w 星球的一个种植园，被分成 m*n 个小格子（东西方向 m 行，南北方向 n 列）。每个格子里种了一株合根植物。

这种植物有个特点，它的根可能会沿着南北或东西方向伸展，从而与另一个格子的植物合成为一体。

如果我们告诉你哪些小格子间出现了连根现象，你能说出这个园中一共有多少株合根植物吗？

5 4
16
2 3
1 5
5 9
4 8
7 8
9 10
10 11
11 12
10 14
12 16
14 18
17 18
15 19
19 20
9 13
13 17
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.
  • 15.
  • 16.
  • 17.
  • 18.

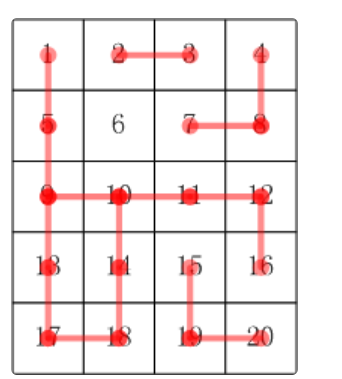
【并查集】合根植物（连通块的数数量）_算法

答案：5

当两个格子出现连根现象时，合并两个格子代表的集合，最后求根节点的个数，即为连通块的个数。

模板：初始化，查找根节点，合并两个节点代表的集合

初始化：每个节点各自为树。

【并查集】合根植物（连通块的数数量）_初始化_02

 

void init(){
  for(i:1~n)dp[i]=i;
}
  • 1.
  • 2.
  • 3.

查找根节点：递归压缩路径

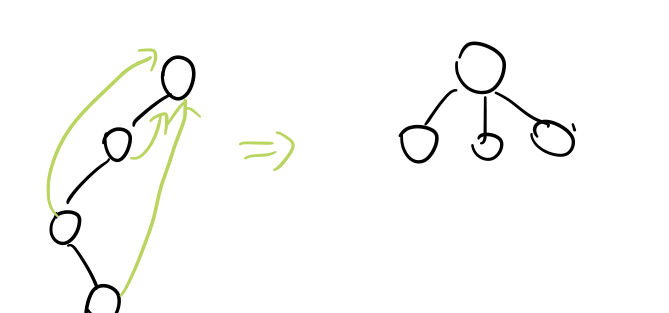
【并查集】合根植物（连通块的数数量）_i++_03

 

int find(int x){
  if(p[x]!=x){
     p[x]=find(p[x]);
  }
  return p[x];
}
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.

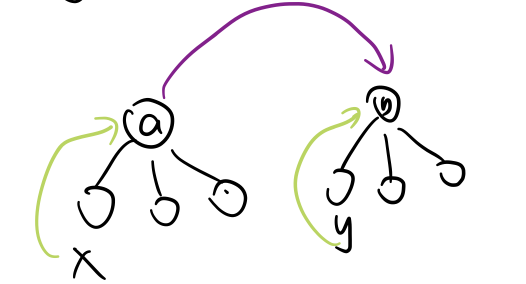
 合并两个节点代表的集合：

【并查集】合根植物（连通块的数数量）_i++_04

 

void join(int x,int y){
  if(find(x)!=find(y)){
     p[find(x)]=find(y);
  }
}
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.

代码：

#include <iostream>
using namespace std;
const int N=1000001;
int n;
int p[N];
void init(){
  for(int i=1;i<=n;i++){
    p[i]=i;
  }
}
int find(int x){
   if(p[x]!=x)p[x]=find(p[x]);
   return p[x];
}
void join(int x,int y){
  if(find(x)!=find(y)){
    p[find(x)]=find(y);
  }
}
int a,b,k;
int main()
{
  cin>>a>>b;
  n=a*b;
  init();
  cin>>k;
  for(int i=0;i<k;i++){
    int x,y;
    cin>>x>>y;
    join(x,y);
  }
  int ans=0;
  for(int i=1;i<=n;i++){
    if(p[i]==i)ans++;
  }

  cout<<ans;

  return 0;
}
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.
  • 15.
  • 16.
  • 17.
  • 18.
  • 19.
  • 20.
  • 21.
  • 22.
  • 23.
  • 24.
  • 25.
  • 26.
  • 27.
  • 28.
  • 29.
  • 30.
  • 31.
  • 32.
  • 33.
  • 34.
  • 35.
  • 36.
  • 37.
  • 38.
  • 39.
  • 40.