半圆阴影_没有办法了，只好用初中数学方法求阴影部分面积了

我在前文：

——《小学六年级奥数：求阴影部分面积》

中留了两道难题，一直惦记于心。今时今日，黔驴技穷，实在不能用“小学数学方法”予以解答，十分苦恼。转念一想，此类题目若是用超出限定范围的方法解答，又会是什么情况呢？便尝试了一下，可以解决了。今日先发一文，给出前文“难题2”的详细分析和解题过程。

题目如下图：

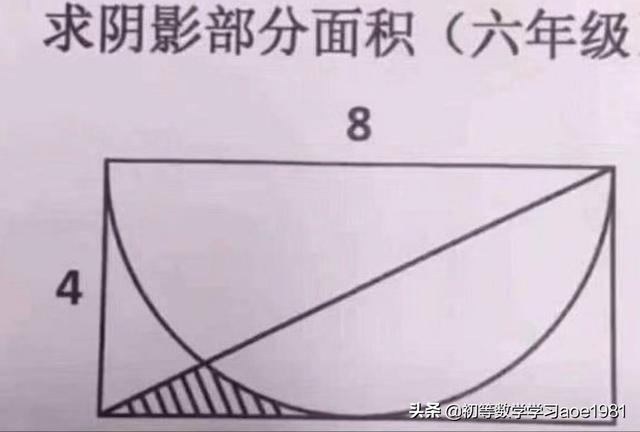
难题2

为了表达的方便，首先作下图：

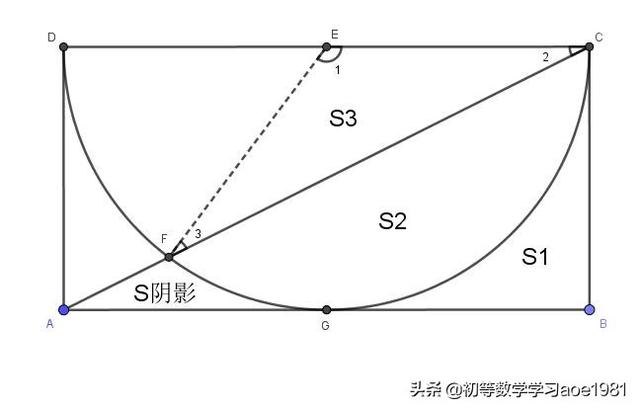
(一)探索思路

①由于：

S阴影＝S△ABC―S1―S2

求解S阴影的问题转化为分别求解：S△ABC、 S1、S2；

②S△ABC＝S长方形ABCD÷2，可解；

③S1＝(S长方形ABCD―S半圆ECGD)÷2，可解；

④由于：

S2＝S扇形ECGF―S3

解题的关键进一步转化为求解圆心角∠1的度数；

⑤由于：

EC＝EF＝半径＝宽

所以：

∠2＝∠3

∠1＝180°―2×∠2

求解∠2的度数变为新的关键；

⑥在RT△ACD中，有：

tan(∠2)＝AD÷CD＝4÷8＝0.5

利用反正切函数即可求得∠2的度数。

(二)解题过程

①∠2＝arctan(AD÷CD)

＝arctan(4÷8)

＝arctan(0.5)

≈26.565051177077989351572193720453°

②∠1＝180°―2×∠2

＝180°―2×26.565051177077989351572193720453°

≈126.86989764584402129685561255909°

③S扇形ECGF＝π×r×r×∠1÷360°

＝3.1415926535897932384626433832795×4×4×126.86989764584402129685561255909°÷360°

≈17.714379484705448048273047362857

④本步根据正弦定理求三角形CEF的面积：

S3＝CE×EF×sin(∠1)÷2

＝4×4×sin(126.86989764584402129685561255909°)÷2

＝6.4

此步中：sin(∠1)＝0.8让我怀疑该题说不定有“小学解”，这个正弦值太凑巧了。本题值得进一步思索。

⑤S2＝S扇形ECGF―S3

＝17.714379484705448048273047362857―6.4

≈11.314379484705448048273047362857

⑥S1＝(S长方形ABCD―S半圆ECGD)÷2

＝(8×4―3.1415926535897932384626433832795×4×4×÷2)÷2

≈3.433629385640827046149426466882

⑦S阴影＝S△ABC―S1―S2

＝8×4÷2―3.433629385640827046149426466882―11.314379484705448048273047362857

≈1.251991129653724905577526170261

(三)回顾反思

本文的解法在两个方面超越了“小学数学方法”范围：

1.利用反三角函数arctan(0.5)表达并计算圆心角∠1的度数；

2.利用正弦定理：

S△ABC＝a×b×sin(C) ÷2＝b×c×sin(A) ÷2＝a×c×sin(B) ÷2

求解三角形CEF的面积。

真心希望有大神出现，能够给出本题的“小学解法”。