STM32平台上的FFT算法实现教程

于 2025-05-01 13:56:54 发布
阅读量870 收藏 25
点赞数 29
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_33557333/article/details/147672752
版权

本文还有配套的精品资源，点击获取 menu-r.4af5f7ec.gif

简介：本文深入探讨了如何在STM32微控制器上实现快速傅里叶变换（FFT）。通过分析"FFT EXAMPLE1_FFTstm32_stm32fft例程_"项目，本文指导开发者理解如何在STM32平台上有效使用FFT算法，包括项目配置、数据采集、FFT计算及结果解析等关键步骤。项目利用STM32 HAL库提供的标准化API，展示了如何通过配置时钟系统、设置ADC参数以及使用FFT库函数等来实现FFT，并对结果进行处理和显示。该项目为嵌入式系统中的复杂数字信号处理提供了实用的实践案例。 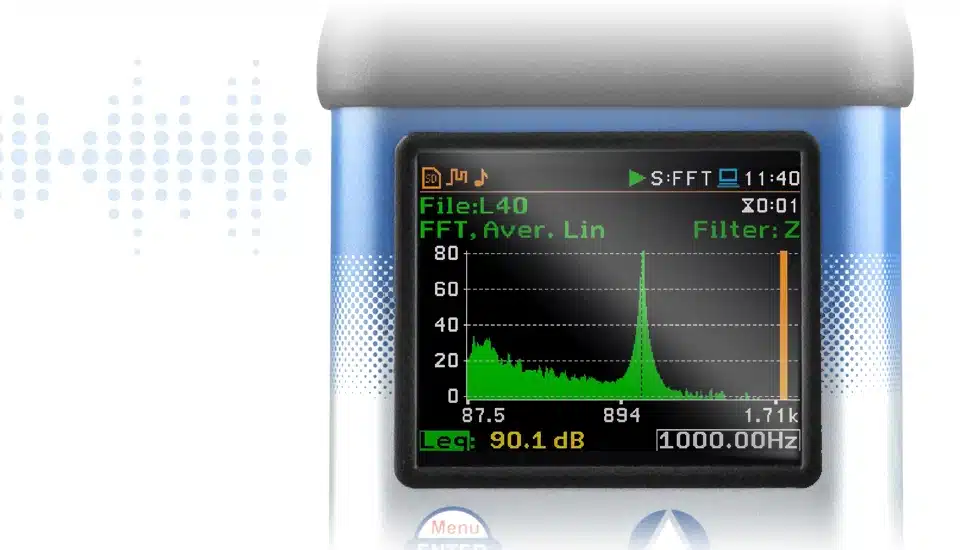FFT

1. STM32微控制器FFT实现

快速傅里叶变换（FFT）是一种在工程和科学领域广泛使用的算法，它能够在微控制器上高效地将时域信号转换为频域信号。对于STM32这样的微控制器，其应用变得尤为重要，因为它能够在硬件层面提供实时信号处理能力，尤其是在资源受限的嵌入式系统中。

在本章中，我们将首先讨论FFT算法在STM32微控制器中的实现基础，包括算法的工作原理和对微控制器性能的影响。我们会介绍STM32的硬件特性，以及如何利用这些特性来优化FFT的运算过程。此外，我们还将探讨STM32的软件环境，包括固件库和编程接口，这对于在STM32平台上成功实施FFT至关重要。

1.1 FFT算法简介

离散傅里叶变换（DFT）是一种基本算法，用于将时域中的有限样本转换为频域。然而，DFT在计算上非常昂贵，特别是当样本数量较多时。FFT是DFT的一种快速实现算法，它通过一种称为“蝴蝶运算”的技巧极大地降低了计算复杂性，使得在资源受限的STM32微控制器上也能进行实时频谱分析成为可能。

1.2 STM32微控制器特性

STM32微控制器系列由STMicroelectronics生产，以其高性能、低功耗和丰富的外设配置而著称。这一系列微控制器内置了浮点运算单元（FPU），这对于执行FFT等复杂的数学运算非常有帮助。同时，STM32还提供了丰富的库函数和硬件抽象层（HAL），这使得开发者能够更加专注于算法的实现，而不是底层硬件的配置细节。

在下一章中，我们将深入探讨一个具体的FFT例程项目，分析其项目结构和工作流程，以及如何在STM32平台上引入和配置STM32FFT库。

2. "FFT EXAMPLE1_FFTstm32_stm32fft例程_"项目分析

2.1 项目概述与目标

2.1.1 STM32FFT库的引入和配置

STM32FFT库是一个针对STM32微控制器优化的快速傅里叶变换（FFT）库。它被引入项目是为了解决复杂信号的频谱分析问题，从而实现快速、准确的频域转换。项目中通过配置FFT库的参数，如采样率、点数（N点FFT）、位反转（bit-reversal）模式等，来适应不同的应用场景。使用STM32FFT库可以避免开发者从零开始编写FFT算法，节省了开发时间，并且确保了算法的性能和准确性。 

#include "arm_math.h"  // 引入FFT库
#define FFT_SIZE 1024   // 定义FFT变换点数

arm_rfft_fast_instance_f32 S; // 实例化FFT结构体
float32_t maxValue = 0;       // 用于存储最大频率值
float32_t maxValue_index = 0; // 最大频率值的索引
float32_t *pSrc;              // 输入数据的指针
float32_t *pDst;              // FFT结果的指针
uint32_t fftSize;             // FFT点数

// 初始化FFT库
arm_rfft_fast_init_f32(&S, FFT_SIZE);
fftSize = S.length;

// 输入数据数组的初始化（示例）
pSrc = (float32_t*)malloc(fftSize * sizeof(float32_t));
pDst = (float32_t*)malloc(fftSize * sizeof(float32_t));

// 填充输入数据，此处省略具体代码...

// 计算FFT
arm_rfft_fast_f32(&S, pSrc, pDst, 0);

// FFT计算结果分析
for (int i = 0; i < fftSize; i++) {
    float32_t real = pDst[2 * i];
    float32_t imag = pDst[2 * i + 1];
    float32_t magnitude = sqrtf(real * real + imag * imag);
    if (magnitude > maxValue) {
        maxValue = magnitude;
        maxValue_index = i;
    }
}
// 最大频率值分析结束

// 清理资源
free(pSrc);
free(pDst);

在上述代码中，我们首先引入了FFT库，并定义了FFT点数，然后实例化了FFT结构体。之后，我们通过 arm_rfft_fast_init_f32 函数初始化FFT库，并在输入数据数组中填充了数据。计算FFT后，我们遍历FFT结果以找到最大幅度的频率分量。

2.1.2 项目结构和工作流程

“FFT EXAMPLE1_FFTstm32_stm32fft例程”项目的结构主要分为几个部分：初始化模块、数据采集模块、FFT计算模块、结果处理模块以及数据展示模块。整个工作流程如下：

  1. 初始化模块 ：设置系统时钟，初始化外设如ADC以及FFT库。
  2. 数据采集模块 ：配置ADC以设定采样率和通道，采集模拟信号，并将其转换成数字信号。
  3. FFT计算模块 ：对采集到的数字信号进行快速傅里叶变换。
  4. 结果处理模块 ：从FFT的结果中提取频谱信息，并进行必要的数值分析。
  5. 数据展示模块 ：将处理后的数据结果展示给用户，如通过LCD显示频谱图。 
graph TD;
    A[开始] --> B[初始化系统时钟];
    B --> C[初始化外设];
    C --> D[配置ADC采样];
    D --> E[启动ADC采集];
    E --> F[读取ADC数据];
    F --> G[执行FFT变换];
    G --> H[结果分析与处理];
    H --> I[数据可视化展示];
    I --> J[结束];

2.2 关键功能模块解析

2.2.1 FFT库函数的作用与调用方式

STM32FFT库提供了多个函数来支持FFT的计算过程，其中关键函数 arm_rfft_fast_f32 用于执行实数的FFT变换。其调用方式非常简单，只需要几个步骤：

  1. 初始化FFT结构体：通过 arm_rfft_fast_init_f32 函数，传入FFT大小和FFT结构体的指针。
  2. 执行FFT变换：使用 arm_rfft_fast_f32 函数，传入初始化的FFT结构体指针，输入数据指针，输出数据指针，以及一个用于指示是否进行位反转操作的标志。
  3. 计算幅值：在得到复数结果后，通过计算实部和虚部的平方和来求得幅值。 
// 初始化FFT结构体
arm_rfft_fast_init_f32(&S, FFT_SIZE);

// 执行FFT变换
arm_rfft_fast_f32(&S, pSrc, pDst, 0);

// 计算幅值
for (int i = 0; i < fftSize; i++) {
    float32_t real = pDst[2 * i];
    float32_t imag = pDst[2 * i + 1];
    float32_t magnitude = sqrtf(real * real + imag * imag);
    // 幅值处理逻辑，此处省略...
}

2.2.2 系统集成点与接口设计

在FFT例程中，系统集成点主要指的是FFT计算模块如何与数据采集模块和结果处理模块相连接。关键的接口设计包括：

  • 数据接口 ：输入为ADC采集的原始数据，输出为FFT计算后的频域数据。
  • 控制接口 ：通过函数调用和参数传递来控制FFT的点数、采样率、是否进行位反转等。
  • 状态接口 ：例如，通过返回值判断FFT是否计算成功，或者是否有错误发生。 
// 示例函数，展示如何从数据采集模块获取数据，并执行FFT计算
void calculate_fft() {
    // 假设 pSrc 是从ADC获取的数据数组
    if (arm_rfft_fast_f32(&S, pSrc, pDst, 0) == ARM_MATH_SUCCESS) {
        // FFT计算成功，执行结果处理
    } else {
        // FFT计算失败，处理错误
    }
}

在上述示例函数 calculate_fft 中，我们首先调用 arm_rfft_fast_f32 函数来执行FFT计算，然后检查其返回值来判断是否成功。如果成功，我们将继续处理结果数据；如果失败，则需要进行错误处理。

本章节中，我们通过代码和逻辑分析的方式，详细介绍了STM32FFT库函数的使用和系统集成点的接口设计。对于一个项目而言，理解这些关键模块的作用和集成方式，对于高效开发和性能优化至关重要。

3. STM32 HAL库使用

3.1 HAL库简介

3.1.1 HAL库与STM32的关系

STM32微控制器系列是STMicroelectronics（意法半导体）推出的一系列基于ARM Cortex-M内核的32位微控制器。随着微控制器技术的发展，对开发工具链和库的要求也越来越高。STM32的硬件抽象层库（HAL）是为了简化软件开发并提供硬件独立性而设计的。HAL库包含了一组丰富的功能，使得开发者可以不必深入理解底层硬件细节，就能控制STM32的各种硬件外设，例如定时器、ADC、DAC、通信接口等。

HAL库与STM32的关系密不可分，它作为一种中间件，让开发者可以直接使用高级的API来操作硬件，而不是直接操作寄存器。这不仅降低了编程难度，还提高了代码的可读性和可维护性。通过使用HAL库，开发者可以更容易地将STM32应用到不同领域和项目中。

3.1.2 HAL库的主要功能和优势

HAL库的主要功能包括：

  • 硬件外设初始化：包括时钟配置、GPIO配置、中断配置等。
  • 硬件外设操作：包括数据的发送和接收、状态检查、错误处理等。
  • 中断和事件处理：支持中断驱动和轮询两种方式，简化中断处理逻辑。
  • 低功耗管理：包括睡眠模式、唤醒源配置、低功耗定时器等。

HAL库的优势在于：

  • 硬件抽象 ：HAL库屏蔽了硬件的差异，同一套代码可以在不同型号的STM32微控制器上运行。
  • 模块化设计 ：HAL库提供的API按照硬件外设功能划分，使得代码更加模块化和可复用。
  • 易用性 ：HAL库的API设计尽量直观易懂，减少了学习成本。
  • 移植性 ：HAL库能够支持不同的IDE环境，如Keil MDK、IAR EWARM、SW4STM32等。
  • 更新支持 ：ST定期更新HAL库，以支持新推出的STM32产品。

3.2 HAL库在FFT例程中的应用

3.2.1 配置时钟和外设

在FFT例程中，为了确保数据采集的准确性和FFT运算的高效性，正确配置时钟和外设至关重要。例如，对于一个基于ADC的信号采集系统，我们需要确保ADC的时钟频率、分辨率、采样率以及触发源都已正确设置。

使用STM32 HAL库，开发者可以轻松配置时钟和外设。以下是一个代码示例，展示了如何使用HAL库来初始化ADC： 

/* ADC init function */
void MX_ADC_Init(void)
{
    ADC_ChannelConfTypeDef sConfig = {0};

    /**Configure the global features of the ADC (Clock, Resolution, Data Alignment and number of conversion) 
    */
    hadc.Instance = ADC1;
    hadc.Init.ClockPrescaler = ADC_CLOCK_SYNC_PCLK_DIV2;
    hadc.Init.Resolution = ADC_RESOLUTION_12B;
    hadc.Init.ScanConvMode = DISABLE;
    hadc.Init.ContinuousConvMode = ENABLE;
    hadc.Init.DiscontinuousConvMode = DISABLE;
    hadc.Init.ExternalTrigConvEdge = ADC_EXTERNALTRIGCONVEDGE_NONE;
    hadc.Init.ExternalTrigConv = ADC_SOFTWARE_START;
    hadc.Init.DataAlign = ADC_DATAALIGN_RIGHT;
    hadc.Init.NbrOfConversion = 1;
    hadc.Init.DMAContinuousRequests = DISABLE;
    hadc.Init.EOCSelection = ADC_EOC_SINGLE_CONV;
    if (HAL_ADC_Init(&hadc) != HAL_OK)
    {
        Error_Handler();
    }
    /**Configure for the selected ADC regular channel its corresponding rank in the sequencer and its sample time. 
    */
    sConfig.Channel = ADC_CHANNEL_0;
    sConfig.Rank = 1;
    sConfig.SamplingTime = ADC_SAMPLETIME_1CYCLE_5;
    if (HAL_ADC_ConfigChannel(&hadc, &sConfig) != HAL_OK)
    {
        Error_Handler();
    }
}

3.2.2 实现数据流的输入输出

数据流的输入输出处理是FFT例程中的核心环节之一。HAL库提供了丰富的函数用于处理输入输出数据流，包括DMA（直接内存访问）相关的API。DMA是STM32微控制器中非常有用的一个功能，它允许外设直接读写内存，而不必通过CPU干预，从而显著提高了数据处理的效率。

以下是一个使用DMA进行ADC数据输入的代码示例： 

/* DMA init function */
void MX_DMA_Init(void)
{
    /* DMA controller clock enable */
    __HAL_RCC_DMA1_CLK_ENABLE();

    /* ADC1 DMA Init */
    hdma_adc1.Instance = DMA1_Channel1;
    hdma_adc1.Init.Direction = DMA_PERIPH_TO_MEMORY;
    hdma_adc1.Init.PeriphInc = DMA_PINC_DISABLE;
    hdma_adc1.Init.MemInc = DMA_MINC_ENABLE;
    hdma_adc1.Init.PeriphDataAlignment = DMA_PDATAALIGN_WORD;
    hdma_adc1.Init.MemDataAlignment = DMA_MDATAALIGN_WORD;
    hdma_adc1.Init.Mode = DMA_CIRCULAR;
    hdma_adc1.Init.Priority = DMA_PRIORITY_HIGH;
    if (HAL_DMA_Init(&hdma_adc1) != HAL_OK)
    {
        Error_Handler();
    }

    __HAL_LINKDMA(&hadc, DMA_Handle, hdma_adc1);

    /* DMA interrupt init */
    /* DMA1_Channel1_IRQn interrupt configuration */
    HAL_NVIC_SetPriority(DMA1_Channel1_IRQn, 0, 0);
    HAL_NVIC_EnableIRQ(DMA1_Channel1_IRQn);
}

在实际应用中，通过合理配置DMA，可以实现持续的数据采集和FFT运算，而不会因为CPU的介入而产生延迟或中断响应的瓶颈。这样不仅能提升数据处理速度，还能确保微控制器资源的合理分配。

4. FFT算法基础

4.1 FFT算法原理

4.1.1 离散傅里叶变换（DFT）概念

离散傅里叶变换（Discrete Fourier Transform，简称DFT）是信号处理领域中非常核心的一个算法。它将时域中离散的信号转换到频域中，使我们能够分析信号的频率成分。具体来说，DFT可以将一个长度为N的复数序列{x(n)}变换到另一个长度也为N的复数序列{X(k)}，其中X(k)是x(n)的频域表示。

DFT的数学表达式如下：

这里，W_N^k = e^(-j2πk/N) 是复数单位根，n和k是整数索引，范围从0到N-1。每个X(k)都是输入序列x(n)的加权和，权重为对应频率的复数指数。

4.1.2 FFT算法的优化思路和步骤

直接计算DFT的复杂度为O(N^2)，这在N较大时非常耗时。快速傅里叶变换（Fast Fourier Transform，简称FFT）算法通过分治策略降低计算复杂度，从而实现了DFT的快速计算。它的核心思想是将大的DFT分解成多个小的DFT，然后合并结果。最著名的FFT算法是由J. W. Cooley和J. W. Tukey在1965年提出的。

FFT算法的关键步骤包括：

  1. 分解：将原始数据序列分成奇数索引序列和偶数索引序列。
  2. 递归：对上述两个序列分别应用FFT算法。
  3. 合并：根据蝶形运算合并结果。

假设我们有N个数据点，FFT算法的复杂度降低到O(NlogN)。对于常见的2的幂次序列，FFT算法尤其高效，这使得它在工程实践中得到了广泛应用。

4.2 FFT算法在信号处理中的应用

4.2.1 频谱分析与信号处理

频谱分析是信号处理中的一个核心应用，它通过分析信号频率成分来解释信号特性。FFT算法使得实时分析和处理信号的频率成分成为可能。通过FFT变换得到的频谱信息可以用来检测信号中的噪声、谐波和调制信息等。

4.2.2 实时数据处理的挑战与对策

在实时信号处理中，FFT算法需要快速且准确地完成变换，这对算法的实现提出了较高要求。为了应对实时数据处理的挑战，需要采取一系列优化对策：

  • 使用定点数代替浮点数，减少计算量并加快执行速度。
  • 利用SIMD指令集并行处理数据。
  • 优化内存访问模式，减少cache miss。
  • 设计高效的缓冲区管理和数据流控制策略。

通过以上措施，可以在保证算法精度的同时，提高FFT算法的处理速度和实时性。下面，我们将通过一个实际代码示例来展示FFT算法的具体实现和优化策略。

5. 数据采集与处理

数据采集与处理是任何数字信号处理项目的核心组成部分，特别是在使用快速傅里叶变换（FFT）进行信号频谱分析时。STM32微控制器由于其丰富的外设和强大的处理能力，经常被用于此类应用。本章将深入探讨数据采集的硬件要求与设置，以及如何在软件层面实现数据处理。

5.1 数据采集的硬件要求与设置

5.1.1 ADC配置与采样速率设定

STM32的模拟数字转换器（ADC）是数据采集的关键部分。为了获得高质量的数字信号，必须正确配置ADC以匹配应用需求。ADC配置涉及多个参数，例如分辨率、采样时间、连续转换模式等。

在STM32中，ADC的初始化和配置通常通过HAL库函数进行。以下是配置ADC的一个基本代码示例： 

/* ADC初始化结构体设置 */
ADC_HandleTypeDef hadc;
hadc.Instance = ADC1;
hadc.Init.ClockPrescaler = ADC_CLOCK_SYNC_PCLK_DIV4;
hadc.Init.Resolution = ADC_RESOLUTION_12B;
hadc.Init.ScanConvMode = DISABLE;
hadc.Init.ContinuousConvMode = ENABLE;
hadc.Init.DiscontinuousConvMode = DISABLE;
hadc.Init.ExternalTrigConvEdge = ADC_EXTERNALTRIGCONVEDGE_NONE;
hadc.Init.ExternalTrigConv = ADC_SOFTWARE_START;
hadc.Init.DataAlign = ADC_DATAALIGN_RIGHT;
hadc.Init.NbrOfConversion = 1;
hadc.Init.DMAContinuousRequests = ENABLE;
hadc.Init.EOCSelection = ADC_EOC_SINGLE_CONV;

/* ADC初始化 */
if (HAL_ADC_Init(&hadc) != HAL_OK)
{
    /* 初始化错误处理 */
}

在该代码段中，我们初始化了一个ADC实例，设置了时钟分频器、分辨率、采样模式等参数，并通过 HAL_ADC_Init 函数启动了ADC初始化过程。

在实际应用中，采样速率的设定取决于所要分析信号的最高频率成分，根据奈奎斯特定律，采样速率必须至少是信号最高频率的两倍。

5.1.2 信号预处理方法

原始信号往往需要预处理才能进行有效的FFT运算。预处理过程可能包括信号滤波、增益调整、信号范围匹配等步骤。例如，可以通过简单的低通滤波器消除高频噪声，或通过增益放大器调整信号幅度以适应ADC的输入范围。

一个简单的数字低通滤波器实现例子如下： 

#define FILTER_TAPS 6 // 滤波器阶数
float filter_coefficients[FILTER_TAPS] = { /* 滤波器系数 */ };
float filter_state[FILTER_TAPS] = { 0 }; // 滤波器状态

void low_pass_filter(float* input, float* output, int length) {
    for (int i = 0; i < length; i++) {
        filter_state[0] = filter_state[1];
        filter_state[1] = filter_state[2];
        filter_state[2] = filter_state[3];
        filter_state[3] = filter_state[4];
        filter_state[4] = filter_state[5];
        filter_state[5] = input[i];
        output[i] = 0;
        for (int j = 0; j < FILTER_TAPS; j++) {
            output[i] += filter_coefficients[j] * filter_state[j];
        }
    }
}

在上面的代码中，我们使用了一个固定系数的FIR滤波器来对输入信号进行低通滤波处理，以减少高频噪声的影响。

5.2 数据处理的软件实现

5.2.1 缓冲区管理和数据流控制

采集到的数据需要被存储在一个缓冲区中，以便进行FFT运算。根据应用场景的不同，缓冲区的管理策略也会有所差异。在实时处理场景中，通常使用循环缓冲区来保持数据流的连续性。

一个基本的循环缓冲区管理策略的实现例子： 

#define BUFFER_SIZE 1024

float buffer[BUFFER_SIZE];
int read_ptr = 0;
int write_ptr = 0;

void buffer_write(float value) {
    buffer[write_ptr] = value;
    write_ptr = (write_ptr + 1) % BUFFER_SIZE;
}

float buffer_read() {
    if (read_ptr == write_ptr) {
        // 缓冲区为空的处理逻辑
    }
    float value = buffer[read_ptr];
    read_ptr = (read_ptr + 1) % BUFFER_SIZE;
    return value;
}

在此实现中， buffer_write 函数用于向缓冲区写入数据，而 buffer_read 函数用于从缓冲区读取数据。读写指针通过取模操作实现循环。

5.2.2 错误检测与异常处理机制

在数据处理流程中，错误和异常的检测是不可或缺的。这包括但不限于缓冲区溢出、数据丢失、非法输入等。为了确保数据处理的鲁棒性，需要在软件中实现错误检测和异常处理机制。

一个简单的错误检测和异常处理逻辑实现示例： 

void process_data() {
    float value;
    if (!is_buffer_full()) {
        value = get_next_data_sample();
        buffer_write(value);
    } else {
        // 缓冲区溢出的处理逻辑
    }
}

bool is_buffer_full() {
    return ((write_ptr + 1) % BUFFER_SIZE) == read_ptr;
}

float get_next_data_sample() {
    // 数据采集逻辑
}

在此例中， process_data 函数检查缓冲区是否已满，以避免数据丢失。如果缓冲区已满，将调用特定的错误处理逻辑。

通过本章节的介绍，我们可以看到，数据采集与处理不仅需要正确的硬件配置和高效的软件实现，还需要完整的错误处理机制来确保数据的准确性和系统的稳定性。接下来的第六章将深入探讨FFT计算的具体步骤与代码示例。

6. FFT计算步骤与代码示例

在信号处理领域，快速傅里叶变换（FFT）是分析频率成分的基本工具。STM32微控制器作为嵌入式领域的明星产品，经常被用来执行实时FFT计算。本章节将详细介绍FFT的计算步骤，并通过代码示例展示如何在STM32上实现FFT。

6.1 FFT计算流程详解

6.1.1 初始化FFT库和算法参数

在FFT计算之前，首先需要初始化FFT库，设置合适的参数以适应特定的应用需求。以下是初始化步骤的详细说明：

  1. 引入FFT库，如 arm_cfft_radix4_instance ，并对其进行初始化。
  2. 根据需要选择正向FFT还是逆向FFT。
  3. 配置FFT的大小，如 1024 点FFT。
  4. 设置输出数据的格式，例如是否进行位反转。

代码示例： 

#include "arm_math.h" /* 包含ARM数学库 */
#define FFT_SIZE 1024 /* FFT点数 */

/* FFT实例初始化 */
arm_cfft_radix4_instance_f32 S;

float32_t real[FFT_SIZE]; /* 存储FFT结果的实部 */
float32_t imag[FFT_SIZE]; /* 存储FFT结果的虚部 */
float32_t output[FFT_SIZE * 2]; /* 存储FFT输出 */

void fft_init() {
    /* FFT初始化 */
    arm_cfft_radix4_init_f32(&S, FFT_SIZE, 0, 1);
}

6.1.2 进行FFT变换的步骤

FFT计算分为几个基本步骤：

  1. 将输入信号的时域数据复制到FFT库的输入数组中。
  2. 调用FFT函数进行变换。
  3. 将变换后的频域数据转换为可读的频谱。

代码示例： 

void fft_compute() {
    /* 复制数据到FFT输入数组 */
    memcpy((void *)output, (void *)real, FFT_SIZE * sizeof(float32_t));
    memcpy((void *)(output + FFT_SIZE), (void *)imag, FFT_SIZE * sizeof(float32_t));

    /* 执行FFT变换 */
    arm_cfft_radix4_f32(&S, output);

    /* 计算每个频点的幅值 */
    arm_cmplx_mag_f32(output, real, FFT_SIZE);
}

6.2 实际代码演示与分析

6.2.1 核心代码段与函数解释

本节中，我们将深入分析上述代码中的关键函数。首先是 arm_cfft_radix4_init_f32 ，用于初始化FFT结构。这个函数需要指定FFT点数、标度因子和是否为逆向FFT。

然后是 arm_cfft_radix4_f32 ，它执行实际的FFT计算。输入参数是初始化后的FFT结构体和复数数据数组。

最后， arm_cmplx_mag_f32 用于计算复数数组的幅值，这是将FFT输出转换为幅谱的过程。

6.2.2 性能分析与优化策略

性能分析是确保FFT模块高效运行的关键步骤。在优化策略方面，可以采取以下措施：

  1. 代码层面优化 ：使用内联函数，减少函数调用的开销。
  2. 数据对齐 ：确保输入输出数据对齐到特定的内存边界，以提高缓存利用率。
  3. 循环展开 ：手动或者使用编译器优化来减少循环开销。

代码层面优化的示例： 

/* 手动循环展开实现计算幅值 */
for (int i = 0; i < FFT_SIZE; i++) {
    real[i] = sqrtf(output[i * 2] * output[i * 2] + output[i * 2 + 1] * output[i * 2 + 1]);
}

以上示例展示了如何在STM32上初始化FFT库，执行FFT计算，并对结果进行初步的性能分析和优化策略的制定。这些步骤和优化技巧对于提高STM32项目中FFT处理的性能至关重要。

接下来的章节中，我们将探讨如何处理FFT计算后的结果数据，包括如何进行后处理和展示，以及结果验证和测试的相关内容。

本文还有配套的精品资源，点击获取 menu-r.4af5f7ec.gif

简介：本文深入探讨了如何在STM32微控制器上实现快速傅里叶变换（FFT）。通过分析"FFT EXAMPLE1_FFTstm32_stm32fft例程_"项目，本文指导开发者理解如何在STM32平台上有效使用FFT算法，包括项目配置、数据采集、FFT计算及结果解析等关键步骤。项目利用STM32 HAL库提供的标准化API，展示了如何通过配置时钟系统、设置ADC参数以及使用FFT库函数等来实现FFT，并对结果进行处理和显示。该项目为嵌入式系统中的复杂数字信号处理提供了实用的实践案例。

本文还有配套的精品资源，点击获取 menu-r.4af5f7ec.gif

codingdie
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值