无限循环小数四则运算_狐狸笔记 | 0.999999无限循环下去，就等于1吗？

前日和12岁的儿子一起学数学。这一章是关于小数，无限循环小数是一个重点。各种循环小数与分数的切换，花式运算，不亦乐乎。

儿子突然在纸头上写了几行式子给我看：

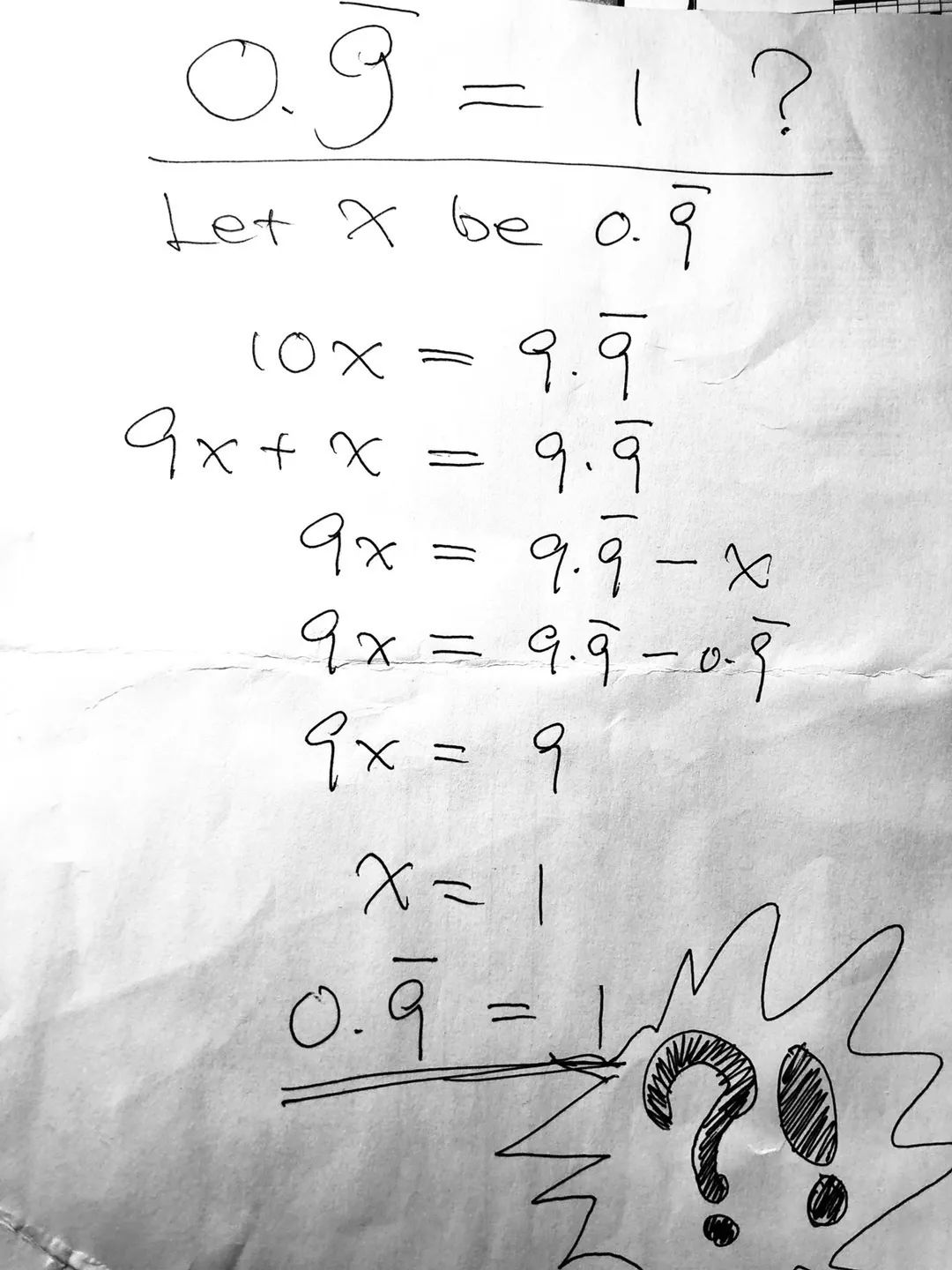
0.999999无限循环就等于1? 不对啊，它只是无限接近1,但怎么会就等于1呢？离1不是还有一点点距离吗？即使这个距离是无限小……

我跟儿子这样争辩。

儿子笑而不语，用铅笔轻轻敲着他写的式子，一脸坏坏的得意。

对啊，他写的推演，看起来也的确是没毛病。何况公式也说了：0.XXXX无限循，就等于X除以9. 那么X如果是9, 那这个数不就等于1了吗？

数学公式和推演，证明了我的常识理解的错误，但我又不理解我的理解错在了哪里。这事奇怪了。

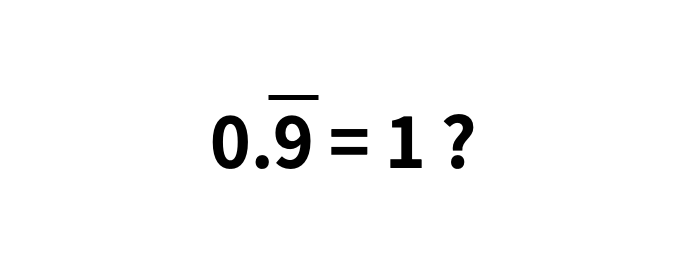
我本人小时虽然数学不错，但也就是高三水平，还是文科班的。自已想不清楚，只能发朋友圈求助。好，这时好戏开场了。

我的朋友圈除了偶尔晒孩有很多点赞外，从来没有这么多激情四射，用心良苦的评论的，应该是创造了“互动率”的纪录。

有意思的是十几位回复的朋友，明显站在两大阵营：

有数学和理科基础的朋友，很多支持“0.9999无限循环=1”的结论。除了上述两种实证方法之外，他们还提出其他的数学推演方法。

但其他人相信这个推演里面有偷换概念的地方，还有很专业的人说：无限循环小数不是definite number (确定数)，而是一个indefinite number (不确定数)，不能使用确切数的四则运算法则，不确定数有自已的计算理论。

(可是如果不能使用四则运算，那数学书里这么多运算，小数分数切来切去加加减减，不就都不成立了吗？)

也有很多人跟我一样，认为0.99999无限循环是无限接近1, 但不是1. 但他们一样无法驳倒数学推演的逻辑。

还是懵圈，于是上百度搜索。哈！原来百度知道上也是吵成一片，跟我朋友圈一样，两派意见各执一词。倒是有个观点有点意思：

0.9999无限循环是否等于1,这是一个不能成立的命题，因为前者是一个不确定的数，后者是一个确定数，二者之间不能谈“等于”的问题。

看了这么多观点，这还是我和儿子之间悬而未决的问题。昨晚回家，他兴冲冲跟我说：他问了学校老师了，0.99999无限循环就等于1.

我去问他课余的数学老师，她也说：就是等于1, 因为数学推演能证明这个结论。

听了这么多人说的不同的观点，要说确切和权威的答案，其实我也并没有。

但一些不确切的想法还是有的 --- 数学本是一个高度抽象的思维方式，演算的规则是抽象的，“极限”这样的概念更是抽象出来的。当用一个抽象的概念加诸于另一个抽象的概念时，就好像是“用数学去证明数学”，也许就会出现某种悖论或是无法解释的漏洞？

这种无法自恰的漏洞，可能是因为数学里运用了模糊和“近似”的思维方法。

比如无限循环小数与分数之间的“等值”关系，也许就是一个抽象和“近似性”思维的体现方式。比如“1/3”和“0.3333无限循环”这两个“数”，“1/3”能代表“将一个东西(数)平均一分为三”的概念，在生活之中是有能对应上的实际存在的概念的；但“0.3333无限循环”则不能代表将一分为三，只代表一个小数点后面一个3无穷延伸下去的“纯抽象概念”。所谓“3的无穷延伸”的概念，只存在于我们的想象和概念化思维之中，在生活中是找不到对应的概念的。

“1/3 = 0.33333无限循环”的论断后面有一个“等值关系”的前提，是一个更加抽象化的数学思维概念。它不去追究两个数分别代表的不同的“意义”，而用近似性的思维，假定二者都有一个“值”，之后才能划这个等号。(其实这个等号也只能说是“约等于”的关系)。

那么“0.99999无限循环=1”的论断，其实一开始就存在一个“建立等值关系”的前提。这个前提出现时，就已暗中自动运用了抽象、近似和模糊化的数学思维(因为“0.99999无限循环”不具备一个确切的“值”，你要论它是不是等值于1，其实就先决了一个条件：你运用近似性原理假定它是有一个“值”的。)

但你也可以不接受这个“等值假定”，也就是看重“0.99999无限循环”这个“数”所代表的概念(而不是“值”)，那么你就不能去谈论“这个数是否等于1”这个话题，因为这个话题没有一个grounding, 也就没有了思考和讨论的可能。

(就好像科学假定宇宙的时间和空间是从大爆炸那个奇点开始的，于是你就不能提出“大爆炸之前宇宙是什么样的？”，因为大爆炸是时间的开始，没有“之前”这个概念。)

所以我暗中怀疑：“0.99999无限循环是否等于1”这个问题，可能涉及到数学原理上的某些Loophole(漏洞)，也就是用数学原理去证明一个抽象的数学概念时，有可能会让这个数学概念偏离了它原始的数学概念，出现某种两边不是人的尴尬状况。

于是：

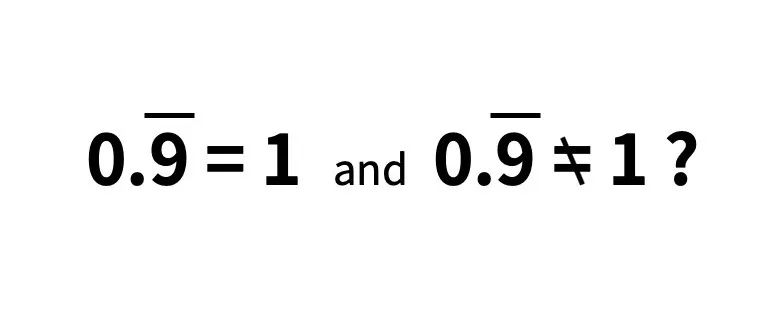
你选择相信左边还是右边，在于你的出发点和立场是怎样。

可以接受这种看起来相互矛盾的结论吗？

当然，我是一个文科生，这都是我完全不专业的臆断。要想提升一个认知高度，一定还得阅读很多数学专著才行。(可是每天忙成这样，哪有时间去找专著来读呢？)

但眼面前，就让我们与这个莫衷于是的问题和平共处吧。“Let’s live with this dilemma, until we find out more in the future.”--- 今晚要去跟儿子这么说。

其实我想让他明白的是：世上并没有那么多黑白分明的确切的答案，你所能获得的答案，往往在于你的立场。而每个人可以站在不同立场，所以很多事都可能是模糊摇摆、自相矛盾而经不起推敲的，你也不得不学会与它们共处。

但重要的不是答案，而是你有没有试图去找那个答案。一件事有没有被推敲过，it makes a big difference.

这种思维习惯，通常叫做“批判性思维”，也叫做“思辩”。

而这，正是“狐狸猎手”这个公号的主旨，所以才想到要写下来这篇笔记。

(当然各位有什么高见，也请在留言区留言，帮我们想得再明白一些也是很有帮助的，谢谢！)