普林斯顿大学公开课 算法1-10：并检查集合-高速整合方法优化

本节介绍了高速综合优化算法。

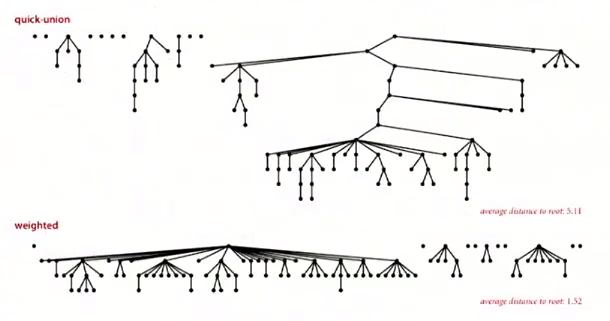
重量的概念，每次操作的时候将重量小的部件挂在重量大的部件之下。

这样就避免了树形结构太高的问题。

下图展示了优化前后的树形结构深度的对照。

证明

能够证明每一个节点的深度最大为lgN。

1. 由于每次合并的时候较小的部件要放在较大的部件之下，所以假设要添加树的高度。每次合并之后，树的大小至少要翻一番。

2. 而N个节点最多仅仅能翻lgN番。

复杂度

这样的算法中合并操作最坏的复杂度为lgN，查询操作最坏情况的复杂度为lgN。

路径压缩

尽管眼下的算法已经可以保证复杂度在lgN下面。可是还有更好的方法。

基本想法就是在查找根节点时，将路径上的全部节点进行路径压缩。仅仅须要一行额外的代码。

使用路径压缩之后查询操作的复杂度是lg*N。lg*是第二种函数，表示的是lgN几次才干达到1。比方lg*16，须要三次lg，lg16=4，lg4=2，lg2=1，所以lg*16=3。

理论上来说查询操作的复杂度不是1，可是实际应用中，这样的算法的复杂度就是1。

结论

尽管现代的超级计算机速度非常快，可是好的算法能节省很多其它的时间。第一种高速查找算法解决一个问题须要30年时间，而如今有了更好的算法。解决相同的问题仅仅须要6秒。

所以，不要期望以后计算机速度快了算法就不须要了。算法是计算机的基础。它永远不会过时。

代码

public  class  UnionFind {

     private  int [] id;

     private  int [] size;

 

     public  UnionFind( int  n) {

         id =  new  int [n];

         size =  new  int [n];

         for ( int  i =  0 ; i < n; i++) {

             id[i] = i;

             size[i] =  1 ;

         }

     }

 

     public  void  union( int  a,  int  b) {

         int  root_a = root(a);

         int  root_b = root(b);

 

         if (root_a == root_b) {

             return ;

         }

 

         // 为了保持树的平衡

         if (size[root_a] < size[root_b]) {

             id[root_a] = id[root_b];

             size[root_b] += size[root_a];

         }  else  {

             id[root_b] = id[root_a];

             size[root_a] += size[root_b];

         }

     }

 

     public  boolean  connected( int  a,  int  b) {

         return  root(a) == root(b);

     }

 

     public  int  root( int  x) {

         while (x != id[x]) {

             id[x] = id[id[x]];  // 路径压缩

             x = id[x];

         }

         return  x;

     }

}

版权声明：本文博主原创文章，博客，未经同意不得转载。