过直线上一点画垂线图_有一点数学话题：尺规作图

尺规作图是什么？

尺规作图能作什么？

为什么直尺要求不带刻度？

尺规作图里有着什么逻辑？

什么是尺规作图三大不能解决难题？

NO.1 什么是尺规作图

顾名思义，就是有限次地利用没有刻度的直尺和圆规来按要求作图。是古希腊的一个数学课题，因趣味性及创造性一直深受人喜爱，时至今日依然是热议的数学话题之一。

为什么要用不带刻度的直尺？难道说条件落后到造不出一个带刻度的尺子了？当然不是，反面来考虑，如果直尺带有刻度，这个话题就变得很普通而又无趣，直接上尺子量就好了，就没什么意思了！

尺规作图所追求的就是利用尽可能少的条件去解决复杂的问题，这样也才能显现我们卓越的智慧。

甚至如果可以的话，连尺子也不要用，实际上确实存在这样的话题：单规作图。

NO.2 从五条公法到基本作图

不管是几何，还是代数，都会有最基本的公理存在，作为我们推断其他结论的理论依据，比如自然数的皮亚诺公理，欧氏几何的五条公设等等，尺规作图也不另外，我们作出的各种各样的图，都可以归根结底到以下5条公法：

(1)根据两个已经确定的点作出经过这两个点的直线。

(2) 以一个已经确定的点为圆心，以两个已经确定的点之间的距离为半径作圆。

(3) 确定两个已经做出的相交直线的交点。

(4)确定已经做出的相交的圆和直线的交点。

(5) 确定已经做出的相交的两个圆的交点。

以上作图简单到你觉得我可能在糊弄你，但我真的没有这个意思，仔细去想，尺规作图作的每一个步骤都是以上五个操作其中之一，任何复杂的作图都都是由基本操作设计组合而成。

数学就是这样由一些公认的基本事实(公理)不断堆砌而成的大厦，地基打得越扎实，楼便能盖得越高。

当然在我们实际作图中考虑的问题是，如何对以上操作设计一个组合，得出解决问题的方案。

接下来，对公法作一个升级，有一些尺规作图的基本作图：

(1)作一条线段等于已知线段

(2)作一个角等于已知角

(3)作已知线段的垂直平分线

(4)作已知角的角平分线

(5)过一点作已知直线的垂线

(6)过一点作已知直线的平行线

(7)过不共线的三点作圆

相信这几个问题对我们来说肯定是小开思了，此处就不一一画图了。由于公法太过朴素，不好用，于是我们设置一些基本作图，为了简化步骤，将作图方案改为由以上基本作图组成而成。

说了这么多，我们好像还没介绍如何根据一个具体的问题去设计作图方案。

不急不急，解决复杂问题前一定得先弄明白我们能作什么，知道自己有什么工具，才能了解能去解决什么问题。

磨刀不误砍柴工，接下来我们看个例子。

NO.3 黄金分割点的作图及分析

问题：已知线段AB，作AB的黄金分割点。

       

问题分析：不妨设线段AB长度为1，构造其黄金分割点即构造一个长度为的线段．

步骤1：取AC中点(构造长为1/2的线段)

          

步骤2：过点B作线段AB的垂线(构造直角)

步骤3：以B点为圆心，BC为半径画圆(构造BD=1/2)

步骤4：连接AD(构造直角三角形ABD)

 

步骤5：以点D为圆心，DB为半径画圆，与AD交于E点．(构造AE=)

步骤6：以A为圆心，AE为半径作圆与AB交于M点，M即为黄金分割点。

NO.4 尺规作图的实质

通过上面的例子，我们可以这么说，所谓的尺规作图，与其说图是画出来的，不如说是算出来的。

尺规作图看似是几何问题，实际上，每一个问题的作图依据都蕴含着代数的运算。正是有这样一步一步精准的计算，才能准确地作出想要的图形。

那是不是任何图都能画？显然不是。什么样的图能画，什么样的图不能画，或者说，具体有运算是可以画出来的？

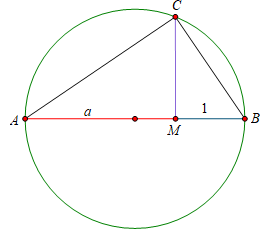
给定两个线段a、b，可作以下：

1、加法：即构造长度为a+b的线段。

2、减法：即构造长度为构造a-b(a>b)的线段。

3、乘法：若想作出线段a·b，则还需给出单位1．若无单位1，则无法知道两者比例，也无法得知两者乘积。

 

如图，置a、b共线，任取非共线一点C使MC=1，作过A、B、C三点的圆，延长CM与圆交点记为D点，根据相交弦定理：MA·MB=MC·MD，MD记为所求线段ab。

4、除法：类似乘法：

将线段1和线段b调换位置，根据MA·MB=MC·MD，即可作出线段a/b。

5、乘方：等同于作乘法，例如a^2=a·a，a的整数次幂均可作。

6、开方：置线段a与线段1共线，以a+1为直径构造圆，过M点作垂线交圆于点C，由射影定理可得：MC=。

总结：给定a、b和单位1，可作加法、减法、乘法、除法、开方五种运算的结果。用加减乘除开方算出的实数，均可用尺规作图作出．并且除此之外的运算，也被证明是不可作。

回顾上面作黄金分割点的例子，其问题即为已知1，作，这里涉及到开方、减法、除法，所以可作。

所以如何去设计作图方案？首先得算出来，然后按照我们上面做加、减、乘、除、开方的方法去画出计算所得的结果就好了呀！

NO.5 正十七边形与三大不能解决难题

高斯同学曾利用尺规作图作出正十七边形，为什么正十七边形可作，在于通过计算发现，正十七边形的内角满足：

观察其内角的余弦值，尽管式子很长且复杂，但是其可通过加减乘除开方得到，并未涉及其他运算，故这样的一个角是可以作出来的，角可作则正十七边形可作，当然作图过程也是比较复杂，此处放个图自行感受一下。

再比如说同为正多边形家族的正七边形却作不了，为啥呢？因为正七边形的内角满足是方程的根，此三次方程求根涉及开立方运算，不在我们尺规作图能力范围之内，无法做出这个角，便无法作出这个图形。

数学史上流传着一个传说，尺规作图有三大未解难题：化圆为方、倍立方体、三等分角。

在基础理论尚未构建完成的时代，总有人想要去证明出来，当我们理解尺规作图的原理，再来看这些问题的时候，他们之所以不可作，就显得非常简单了。

1、化圆为方：作一个面积与已知圆相等的正方形。设给定圆的半径为1，则面积为π，若要作一个正方形的面积和此圆相等，则正方形边长为，即问题变成：已知1作，因为π是超越数(上一篇提过)，故不可作。

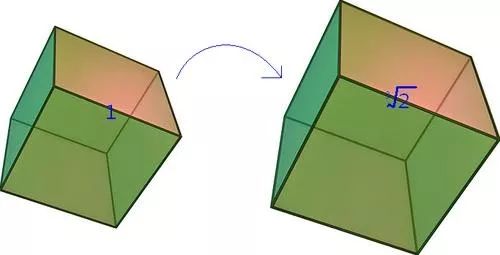
2、倍立方体：已知一个立方体，作一个体积等于其两倍的立方体。设给定立方体边长为1，则体积为1，作一个体积为2的立方体即构造长度为三次根号2的线段，前面我们已经讲了仅能作开平方，并不能作开立方，故不可作。

3、三等分角：任意给一个角，对其作三等分。这个问题等价于已知cosA，求方程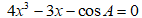的根，根据三次方程的公式解可以发现，一般性的三次方程其结果仅仅是二次根号是表示不出来的，故不可作。

谢谢阅读，以上都是瞎编的。

你点的每个赞，我都认真当成了喜欢