POJ 1149 PIGS (AC这道题很不容易啊)网络流

PIGS

Description

Mirko works on a pig farm that consists of M locked pig-houses and Mirko can’t unlock any pighouse because he doesn’t have the keys. Customers come to the farm one after another. Each of them has keys to some pig-houses and wants to buy a certain number of pigs.
All data concerning customers planning to visit the farm on that particular day are available to Mirko early in the morning so that he can make a sales-plan in order to maximize the number of pigs sold.
More precisely, the procedure is as following: the customer arrives, opens all pig-houses to which he has the key, Mirko sells a certain number of pigs from all the unlocked pig-houses to him, and, if Mirko wants, he can redistribute the remaining pigs across the unlocked pig-houses.
An unlimited number of pigs can be placed in every pig-house.
Write a program that will find the maximum number of pigs that he can sell on that day.
Input

The first line of input contains two integers M and N, 1 <= M <= 1000, 1 <= N <= 100, number of pighouses and number of customers. Pig houses are numbered from 1 to M and customers are numbered from 1 to N.
The next line contains M integeres, for each pig-house initial number of pigs. The number of pigs in each pig-house is greater or equal to 0 and less or equal to 1000.
The next N lines contains records about the customers in the following form ( record about the i-th customer is written in the (i+2)-th line):
A K1 K2 … KA B It means that this customer has key to the pig-houses marked with the numbers K1, K2, …, KA (sorted nondecreasingly ) and that he wants to buy B pigs. Numbers A and B can be equal to 0.
Output

The first and only line of the output should contain the number of sold pigs.
Sample Input

3 3
3 1 10
2 1 2 2
2 1 3 3
1 2 6
Sample Output

7

题意：
输入第一行给你n个猪圈，m个顾客。
第二行n个数，分别表示第i个猪圈里有多少头猪。
然后后m行，每行第一个数表示第i个人有k把钥匙，后k个数为他的钥匙能开的猪圈标号。最后一个数表示他需要多少头猪。
所有开着门的猪圈里的猪能相互串。（人买走猪后就把猪圈锁上了）
求最多能卖多少头猪。

思路：
一开始 没有思路，想了好久，终于建好图了（细节请见代码注释） 。接着就无限WA。WA。WA。憋了一下午。晚上李队长帮忙挑错，后来LH也加入挑错的行列，挑了1h，才挑出来。（对拍拍了快1000组数据也没有拍出错）。
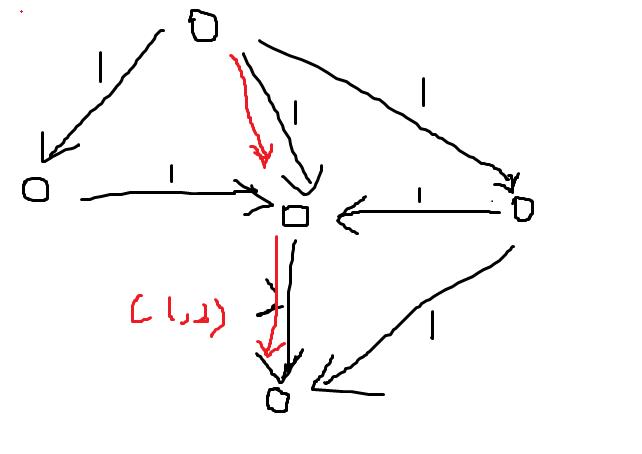
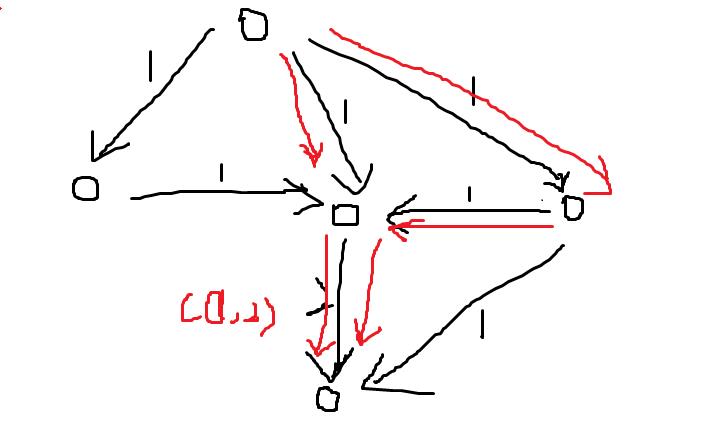
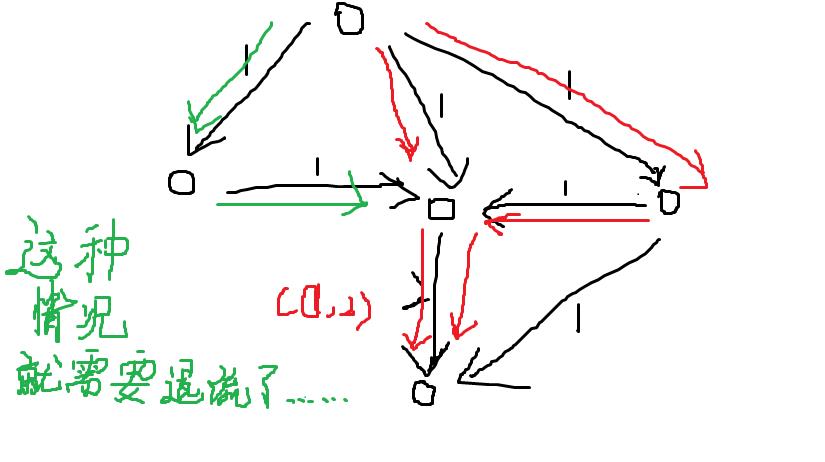
原来是我没有建反向的流。反向流是无论什么情况都要建的。。
下面是需要返向流的原因。
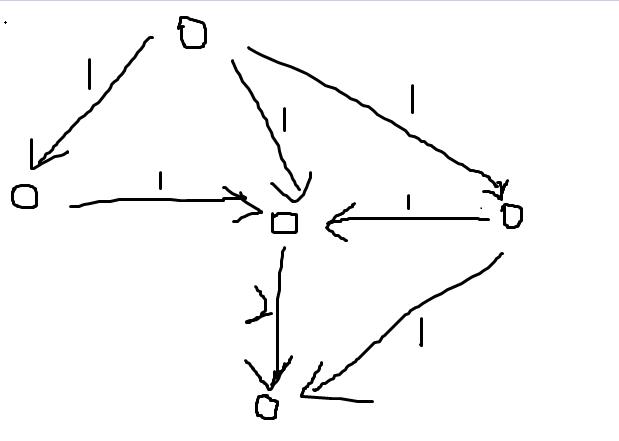
假设有个这个图。

这个图如果不建反向流的话就是错的。然而对拍拍不出来。。。

#include <queue>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int houses,customers,num[2005],vis[2005],tot=0,a[2005],jy,p[2005];
int first[2005],nxt[2005*2005],w[2005*2005],v[2005*2005];
void add(int from,int to,int weight)//ATTENTION!!!!!!需要建反向边！！！ (多谢LH大神的指点)
{
    v[tot]=to;w[tot]=weight;//否则是没有办法回溯的  无论是不是DAG都是这样。。。 
    nxt[tot]=first[from];
    first[from]=tot++;
    v[tot]=from;w[tot]=0;
    nxt[tot]=first[to];
    first[to]=tot++;
}
int maxflow()
{
    queue<int>q;int f=0;
    while(1)
    {
        memset(vis,0,sizeof(vis));
        memset(a,0,sizeof(a));
        q.push(0);vis[0]=1;a[0]=0x3fffffff;
        while(!q.empty()){
            jy=q.front();q.pop();
            for(int i=first[jy];~i;i=nxt[i]){
                if(!vis[v[i]]&&w[i]){
                    vis[v[i]]=1;
                    a[v[i]]=min(a[jy],w[i]);
                    p[ v[i] ]=i;//找 上次 改流的边   。。。 
                    q.push(v[i]);
                }
            }
        }
        if(a[2004]==0)break;
        for(int i=2004;i;i=v[ p[i]^1 ]) 
            w[ p[i] ]-=a[2004],w[ p[i]^1 ]+=a[2004];//反向边要  “－ ”
        f+=a[2004];
    }
    return f;
}
int main()
{
    scanf("%d%d",&houses,&customers);// houses 1 <= M <= 1000  customers  1 <= N <= 100
    memset(first,-1,sizeof(first));
    for(int i=1;i<=houses;i++)
        scanf("%d",&num[i]);
    for(int i=1;i<=houses;i++)//建一个超级源点“0”。 
        add(0,i,0x3fffffff);
    int A,B,xx;
    for(int i=1006;i<=customers+1005;i++)//第i个customer
    {
        scanf("%d",&A);
        for(int j=1;j<=A;j++)//第i个customer 拥有的钥匙 
        {
            scanf("%d",&xx);//钥匙号
            if(!vis[xx])//如果没有被打开过，直接把猪圈和商人之间连上边权为猪圈里面猪的数量的边 
                vis[xx]=i,add(xx,i,num[xx]);//xx---->猪圈号    i----->商人号  
            else//如果它被打开过，把打开过该猪圈的最后一个商人和此商人连边。 
                add(vis[xx],i,0x3fffffff),vis[xx]=i;//vis[xx]----> 打开过该猪圈的最后一个商人！最后一个商人！否则是错的（多谢李队长指点。。。） 
        }
        scanf("%d",&B);
        add(i,2004,B);//设点2004为超级终点
    }
    printf("%d\n",maxflow());
}

一下午+一晚上 。。。。

转载于:https://www.cnblogs.com/SiriusRen/p/6532477.html