MATLAB工具-PolyhedronInertialProperties：计算多面体惯性特性

本文还有配套的精品资源，点击获取

简介：MATLAB中的"PolyhedronInertialProperties"工具用于计算多面体的质量矩、转动惯量和质心位置。这些惯性特性对于理解物体在运动中的动力学行为至关重要，尤其在机械工程、航空航天和机器人学等领域。计算过程包括定义多面体的几何描述、计算质量、质心位置，以及转动惯量和质量矩。该工具简化了复杂计算过程，用户可以通过输入顶点和面信息获得惯性矩阵和质心位置，同时包含数据导入和分析功能。使用该工具需要遵守 license.txt 文件中的条款，且可能包含附加文件 polyhedronzip 以提供进一步的帮助和支持。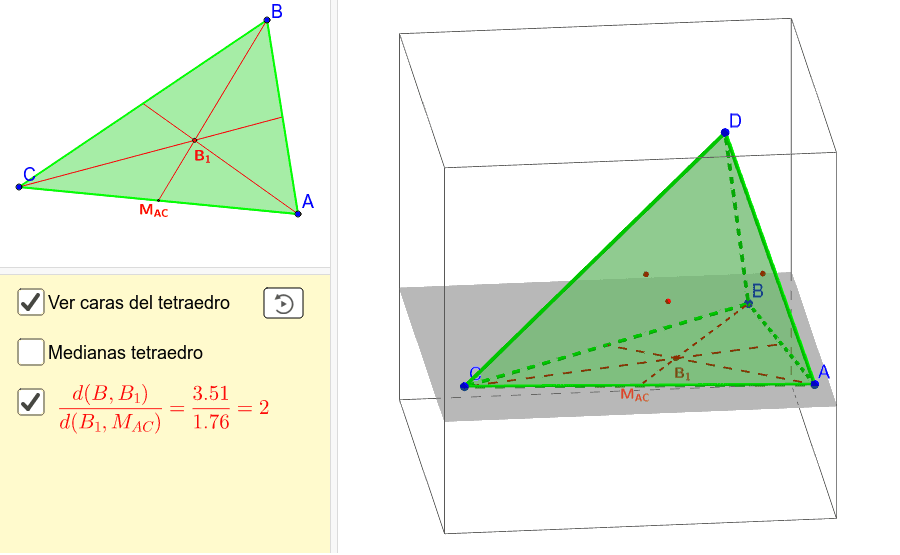

1. MATLAB工具-PolyhedronInertialProperties概述

1.1 PolyhedronInertialProperties简介

在工程设计与分析领域，对多面体物体的惯性特性进行准确计算是至关重要的。MATLAB作为一款强大的数学计算与仿真平台，提供了名为PolyhedronInertialProperties的工具箱，旨在简化这一复杂过程。该工具能够通过数学算法快速求解多面体的质量特性，包括质心位置和转动惯量，大大提高了工程师在机械设计和材料分析等工作中的效率。

1.2 工具特点与适用范围

PolyhedronInertialProperties主要面向机械、航天、汽车等领域的工程师和研究人员。它不仅适用于规则的几何形状，甚至可以处理复杂的非规则多面体。通过对多面体的顶点、边和面进行定义，该工具能够直观地展示出物体的惯性特性，为工程设计提供理论支持和验证依据。

1.3 应用前景与展望

随着技术的不断进步，MATLAB工具箱的多项功能持续优化，PolyhedronInertialProperties的精确性和易用性也在不断增强。未来，它将更加广泛地应用于快速原型设计、高精度仿真、以及优化算法中，成为工程师手中不可或缺的工具。

2. 多面体定义及其在工程中的应用

2.1 多面体的数学定义与特性

2.1.1 几何基础和顶点、边、面的关系

多面体是三维空间中的一个几何体，它由多个平面（称为面）的边界构成，这些平面边界的交集形成线段（称为边），多个边的交点形成顶点。多面体的特点是其每一个面都是一个凸多边形，且任何一个顶点的所有面都可以构成一个锥体，锥体的顶点位于多面体外部。

数学上，我们可以用顶点、边、面的数目来描述一个特定的多面体。一个典型的多面体公式是欧拉公式，即 V - E + F = 2，其中V是顶点数，E是边数，F是面数。此外，多面体的对偶多面体是将原多面体的每一个面变为顶点，每一个顶点变为面，并保持边的连接关系得到的。

一个多面体的几何结构可以用顶点集合V、边集合E和面集合F来描述。例如，对于一个立方体，V = {V1, V2, ..., V8}，E = {E1, E2, ..., E12}，F = {F1, F2, ..., F6}。

2.1.2 多面体在现实世界中的对应物

在现实世界中，多面体的对应物可以是自然界中发现的晶体结构、工程结构中的支撑框架，或者是艺术和建筑设计中用到的几何形状。例如，煤炭和钻石晶体的结构可以看作是多面体的实例；桥梁和塔架的设计往往采用多面体结构以提高结构的稳定性和强度。

多面体在各种应用中的重要性在于其能够以最小的表面积包含最大的体积，这在材料科学和工程设计中非常有用，因为它可以优化材料的使用并减轻结构的重量。

2.2 工程应用中的多面体建模

2.2.1 多面体在机械结构设计中的应用

多面体在机械结构设计中的应用可以追溯到古代，当时人们就利用几何形状来构建稳固的结构。在现代工程中，多面体被用于设计具有复杂几何形状的部件，这些部件可以通过有限元分析等数值方法进行强度和耐久性测试。

例如，使用计算机辅助设计（CAD）软件，工程师可以构建多面体模型来模拟汽车车身、飞机机翼和其他复杂组件的结构。这些模型的多面体表示可以精确地反映实际物体的几何特性，为后续的材料选择、应力分析和制造过程提供依据。

2.2.2 多面体在材料科学和工程分析中的角色

在材料科学领域，多面体结构在材料的微观建模中起着关键作用。多面体可以用来模拟各种多孔材料、合金、以及复合材料中的颗粒结构。通过对这些结构的建模和分析，研究人员能够预测材料的力学、热学和电磁性能。

工程分析中，多面体模型被用于模拟和优化结构的性能，例如通过有限元分析（FEA）来评估应力集中和裂纹扩展。此外，多面体的对称性原则在工程中被用来设计均匀分布载荷的结构，以及通过拓扑优化来减少材料的使用。

graph TD
    A[开始] --> B[确定多面体几何]
    B --> C[应用CAD进行设计]
    C --> D[进行数值分析]
    D --> E[材料性能预测]
    E --> F[结构优化]
    F --> G[最终设计确认]

上述流程图展示了多面体在工程设计中的一般应用流程。从确定多面体的几何结构开始，利用CAD软件进行设计，然后进行必要的数值分析，以此来预测材料性能并优化结构设计。最终通过不断迭代来确认最佳设计方案。

在实际操作中，机械工程师和材料科学家会使用专业的CAD和CAE（计算机辅助工程）软件来处理复杂的多面体模型。例如，使用ANSYS进行有限元分析，或者使用SolidWorks来创建和修改多面体模型。

flowchart LR
    A[确定多面体几何] -->|CAD软件| B[构建3D模型]
    B -->|有限元分析| C[应力、热、电磁分析]
    C -->|材料选择| D[性能预测和结构优化]
    D -->|迭代改进| E[验证模型]
    E -->|产品实现| F[最终设计确认]

通过这个流程图，我们可以看到一个从确定多面体几何结构到产品最终实现的详细过程。每个步骤都经过精心设计和计算，确保最终的设计能够在各方面达到预期性能。

3. 惯性特性的计算步骤：

3.1 多面体几何描述的输入方法

3.1.1 数值输入与图形界面输入的比较

在确定多面体的惯性特性时，输入描述是至关重要的第一步。目前，主要有数值输入和图形界面输入这两种方法。数值输入，顾名思义，是通过编写代码或者使用表格的形式直接给出多面体各个顶点的坐标、边的连接关系以及面的构成。这种方法的优点是对于计算机来说易于处理，可以快速转换为内部数据结构。然而，对于人类用户来说，特别是缺乏编程背景的用户，这种方法显得不够直观，容易出错。

与数值输入相对的是图形界面输入。这种方法借助于交互式的图形界面，让用户可以直观地通过鼠标点击、拖拽等操作来定义多面体的各个面、边和顶点。显然，这种方法对用户更加友好，特别是对于设计人员和工程师来说，它能更快地得到所需模型。但图形界面生成的模型往往需要额外的步骤来转换为计算机能够理解的格式。

3.1.2 输入数据的预处理与验证

无论采用数值输入还是图形界面输入，输入的数据都必须经过预处理和验证。预处理的目的是为了提高数据的准确性和一致性，例如，去除重复的顶点、调整顶点坐标精度等。验证则需要确认输入数据的几何结构是否完整且无逻辑错误。比如，每一条边的端点必须是已定义的顶点，每一个面都必须能被真实地在三维空间中构建出来，等等。

在实际操作中，可以设计一系列的算法来自动完成这些工作。例如，使用某种排序算法对顶点进行排序以消除重复；对边和面进行遍历来检查它们的有效性等。一些高级的工具还能够提供自动修复功能，对于小的不一致之处能够自动纠正，从而提升用户体验。

3.2 质量和质心位置的计算方法

3.2.1 质量的确定与密度分布的关系

在计算多面体的惯性特性时，质量是一个关键参数。实际中，多面体的质量通常由材料的密度和体积来决定。对于一个均质多面体，其密度在任何位置都是一致的，因此可以通过体积乘以密度来直接计算质量。对于非均质多面体，质量的计算就更为复杂。可能需要根据材料的密度分布，将多面体分割成小的单元，再对每个单元的质量进行计算，最后进行累加。

为实现这样的计算，可以使用数值积分方法，比如在MATLAB中使用 integral 或 quad 函数对体积内的密度函数进行积分。这样，即便密度在不同位置有复杂的函数关系，也能准确计算出质量。代码示例如下：

% 定义多面体体积内某位置的密度函数，例如ρ(x,y,z)
density_func = @(x,y,z) x.^2 + y.^2 + z.^2; % 示例密度函数

% 定义体积积分的限制，例如在多面体界定的区域内
x_limits = [0, 1];
y_limits = [0, 1];
z_limits = [0, 1];

% 计算质量
mass = integral3(density_func, x_limits(1), x_limits(2), y_limits(1), y_limits(2), z_limits(1), z_limits(2));

disp(['计算得到的多面体质量为：', num2str(mass)]);

3.2.2 质心位置的几何计算与物理意义

质心的位置决定了多面体旋转和移动时的物理行为。对于一个由若干顶点和面组成的多面体，其质心可以通过几何方法计算得到。具体来说，就是将每个顶点的质量（或体积）乘以它们到某一个原点（通常取多面体的一个顶点）的距离，然后对所有顶点进行积分求和，最后除以总质量，得到的即是质心的位置。

在代码实现上，我们可以按照以下步骤进行：

% 假定顶点坐标和各顶点的质量
vertices = [0 0 0; 1 0 0; 0 1 0; 0 0 1]; % 顶点坐标
masses = [1; 1; 1; 1]; % 假定每个顶点的质量

% 计算各顶点的坐标与原点的乘积向量
moment_vector = cross(vertices, masses .* vertices);

% 计算质心
total_mass = sum(masses);
centroid = moment_vector / total_mass;

disp(['计算得到的多面体质心位置为：', num2str(centroid)]);

质心位置的计算不仅在理论上有重要意义，而且在实际应用中也非常关键。例如，在航天工程和机器人学中，计算质心是必不可少的一步。

3.3 转动惯量和质量矩的计算方法

3.3.1 转动惯量的理论基础和计算公式

转动惯量是描述物体转动惯性大小的物理量，它与物体的质心位置、质量分布以及旋转轴的位置有密切关系。计算公式为：

[ I = \sum_{i=1}^{n} m_i \cdot r_i^2 ]

其中，(I)是转动惯量，(m_i)是每个质点的质量，(r_i)是每个质点到旋转轴的垂直距离。在连续介质中，可以将其转换为积分形式：

[ I = \int_V \rho(r) \cdot r^2 \cdot dV ]

在MATLAB中，我们可以使用 integral3 函数对体积内的每个点进行积分计算转动惯量。代码如下：

% 质量分布函数（示例）
density_func = @(x,y,z) x.^2 + y.^2 + z.^2;

% 转动惯量的积分计算
% 假设绕z轴旋转，计算公式为：I = ∫∫∫ρ(x,y,z) * (x^2 + y^2) dxdydz
inertia_z = integral3(density_func, x_limits(1), x_limits(2), y_limits(1), y_limits(2), z_limits(1), z_limits(2));

disp(['绕z轴的转动惯量为：', num2str(inertia_z)]);

3.3.2 质量矩的定义及其对称性原则

质量矩是指多面体质量相对于某一点的分布情况。在物理学中，质量矩可以被看作是物体对某一点的“质量距离”乘积。一个常见的应用是，要计算一个物体相对于其质心的质量矩，这有助于了解其旋转的动态行为。质量矩的计算公式为：

[ M = \sum_{i=1}^{n} m_i \cdot d_i ]

其中，(M)是质量矩，(m_i)是每个质点的质量，(d_i)是每个质点到某点（通常是质心）的向量。

对于对称性较高的物体，质量矩有许多简化计算的规则，比如对于轴对称的物体，垂直于对称轴的质量矩分量将为零。在实际应用中，利用对称性可以显著减少计算量。例如，对于一个立方体，可以证明其绕通过中心且平行于面的轴的转动惯量是相同的，这称为转动惯量的主轴定理。

在MATLAB中，我们可以通过遍历多面体的面、边和顶点来计算质量矩：

% 计算质量矩
% 假定中心点为原点
moment = sum(vertices .* masses);

disp(['多面体相对于原点的质量矩为：', num2str(moment)]);

通过上述方法，我们不仅能够计算出转动惯量和质量矩，还能够理解和应用它们在物理世界中所扮演的角色。这些计算为模拟和分析多面体在不同场景下的动态行为提供了基础。

4. 许可证文件 license.txt 的重要性

4.1 软件许可与版权法律

在IT行业中，软件许可与版权法律是维护开发者权益和确保用户合法使用软件的关键。了解这些法律和规范有助于确保企业和个人在使用软件时避免潜在的法律风险。

4.1.1 许可证文件的法律意义和作用

许可证文件通常被称为 license.txt ，它定义了软件的使用条款和条件。 license.txt 文件通常包含了软件使用许可的详细条款，包括但不限于：

• 许可类型（比如个人使用、商业使用、教育使用等）
• 许可的限制（如禁止转售、修改或逆向工程）
• 版权声明和归属信息
• 软件分发和维护的相关政策

这个文件是企业与用户之间的一个法律契约，规定了用户在不违反法律的前提下，可以如何使用该软件。一个有效的许可证协议可以防止软件被滥用，并为开发者的劳动成果提供保护。

4.1.2 软件盗版的风险和法律后果

软件盗版是指未经授权非法复制、分发或使用软件的行为。除了道德上的谴责，软件盗版还可能带来严重的法律后果：

• 对个人用户，他们可能面临民事诉讼、索赔或罚款。
• 对企业用户，除了罚款和法律诉讼，还可能导致商誉损失和市场份额下降。
• 对开发者和软件公司，盗版意味着潜在的收入损失和创新动力的削弱。

因此，确保用户了解并遵守 license.txt 文件中的条款是至关重要的。软件许可维护了软件生态系统的公平性和可持续性，保障了所有利益相关者的利益。

4.2 license.txt 在软件安装和使用中的作用

license.txt 文件在软件的安装和使用过程中扮演着重要角色。它确保用户在软件安装前已经阅读和同意了软件的使用条款。

4.2.1 许可证文件的验证流程

在安装现代软件时，通常会有一个步骤提示用户接受或拒绝许可协议。这个流程一般包括：

1. 安装程序会在开始安装之前提示用户阅读 license.txt 文件。
2. 用户必须点击“我接受条款”或类似的按钮来继续安装过程。
3. 如果用户拒绝接受，则安装程序会中止。

验证流程保证了用户对软件的使用是基于明确的法律理解和同意之上的，这样可以防止法律纠纷的发生。

4.2.2 许可证问题对软件功能的限制

如果用户未遵循许可证条款，软件可能会通过多种方式施加限制，以保证许可证的有效性和合规性：

• 软件可能仅提供有限的功能或试用期。
• 一些功能可能需要额外的授权。
• 在一些极端情况下，软件可能会停止工作。

这些限制在法律上是必要的，确保软件提供者能够控制和监督软件的合法使用情况。

总结来说， license.txt 文件在确保软件合法使用方面起到了至关重要的作用。它不仅为软件开发者和用户之间提供了一种法律上的保障机制，也为合法的软件使用设定了明确的边界。理解并遵守软件许可协议，是每一位IT专业人士和用户应该具备的基本素质。

5. polyhedronzip 文件的内容和作用

5.1 polyhedronzip 文件的结构和组成

polyhedronzip 文件是一种特定格式的压缩文件，广泛应用于多面体惯性特性分析软件中。它能够有效地存储和传输多面体相关的几何数据、材质属性以及计算结果。了解 polyhedronzip 文件的结构和组成，对于用户来说是非常重要的，这有助于更好地利用这些文件，无论是进行数据备份还是在多面体分析中使用。

文件压缩的必要性和优势

在存储和传输过程中，使用 polyhedronzip 文件可以大大减少所需的磁盘空间和网络带宽。在一些极端情况下，这能够减少数百倍的数据量。除了节省空间，压缩数据还有助于减少备份时间，以及提高数据传输的效率和安全性。此外，压缩可以提供一种方式来保护数据不被未经授权的访问，因为只有知道如何解压缩的用户才能访问文件内容。

常见的文件压缩工具和技术

polyhedronzip 文件的压缩通常使用特定的算法和工具来实现。这类工具通常提供高性能的压缩率和恢复速度，同时保证了数据的完整性。一些常见的压缩工具包括但不限于7-Zip、WinRAR和Zstandard等。这些工具运用如哈夫曼编码、LZ77、LZ78或其变种等先进的压缩算法，这些算法通过查找并消除数据中的冗余部分来降低文件大小。

5.2 polyhedronzip 在数据备份与传输中的应用

数据备份与传输是IT环境中最常见的任务之一，尤其是在需要处理大量多面体数据时。 polyhedronzip 文件在此过程中扮演着重要角色，它们提供了在备份和传输中节省资源和增强安全性的手段。

数据压缩与备份的策略

使用 polyhedronzip 文件进行数据备份时，管理员可以制定策略，定期备份软件生成的多面体数据。这种策略通常包括选择压缩级别、确定备份时间以及备份文件的存放位置。压缩级别不同，压缩效率和速度也会有所不同，选择合适的级别对于平衡备份时间与节省空间至关重要。

文件传输时的安全性和完整性检查

数据传输是文件管理中另一个关键环节。通过使用 polyhedronzip 文件，可以将数据打包成一个压缩包，减少了传输时的潜在风险。因为传输前通常会对文件进行加密，这样即便是数据在传输过程中被截获，没有解压缩密码的人也无法获取数据内容。同时，一些压缩工具还支持对压缩文件进行校验，如使用MD5或SHA算法来生成校验码，确保文件在传输过程中未被篡改。

5.3 polyhedronzip 的实践操作指南

在实践中，用户可能需要根据不同的需求来压缩或解压缩 polyhedronzip 文件。下面将详细介绍如何使用命令行工具和图形界面工具来操作 polyhedronzip 文件。

使用命令行解压缩 polyhedronzip 文件

对于熟悉命令行的用户来说，使用诸如7z、unzip这样的命令行工具可以快速地执行压缩或解压任务。以下是使用命令行解压缩 polyhedronzip 文件的一个示例：

# 解压缩 polyhedronzip 文件到指定目录
7z x path/to/polyhedronzipfile.phz -ooutput_directory

该命令中， x 代表解压缩操作， path/to/polyhedronzipfile.pzh 是需要解压缩的文件路径， output_directory 则是解压后的文件存放目录。

图形界面工具解压缩 polyhedronzip 文件的步骤

对于习惯使用图形界面的用户，可以借助如WinRAR或7-Zip这类具有图形界面的工具来操作压缩文件。以下是使用图形界面工具进行解压缩的一般步骤：

1. 打开图形界面工具。
2. 选择“解压缩”功能。
3. 浏览并选择 polyhedronzip 文件。
4. 指定解压缩的目标目录。
5. 开始解压缩过程。

通过这样的步骤，用户可以轻松地管理和操作 polyhedronzip 文件，从而有效地备份和传输相关数据。

通过本章节的介绍，读者应能够理解 polyhedronzip 文件的重要性和实用性，以及如何在实际工作中对其进行操作。对于多面体惯性特性分析的专业人士来说，这些知识不仅有助于日常工作的顺利进行，还能确保数据的安全性和高效性。

本文还有配套的精品资源，点击获取

简介：MATLAB中的"PolyhedronInertialProperties"工具用于计算多面体的质量矩、转动惯量和质心位置。这些惯性特性对于理解物体在运动中的动力学行为至关重要，尤其在机械工程、航空航天和机器人学等领域。计算过程包括定义多面体的几何描述、计算质量、质心位置，以及转动惯量和质量矩。该工具简化了复杂计算过程，用户可以通过输入顶点和面信息获得惯性矩阵和质心位置，同时包含数据导入和分析功能。使用该工具需要遵守 license.txt 文件中的条款，且可能包含附加文件 polyhedronzip 以提供进一步的帮助和支持。

本文还有配套的精品资源，点击获取