算法学习(1)----扩展欧几里得算法

最新推荐文章于 2021-01-27 11:13:09 发布

weixin_33831196

最新推荐文章于 2021-01-27 11:13:09 发布

阅读量92

点赞数

原文链接：http://www.cnblogs.com/dongling/p/5716410.html

版权

摘自百度百科

欧几里德算法

欧几里德算法又称辗转相除法，用于计算两个整数a,b的最大公约数。其计算原理依赖于下面的定理：

gcd函数就是用来求(a,b)的最大公约数的。

gcd函数的基本性质：

gcd(a,b)=gcd(b,a)=gcd(-a,b)=gcd(|a|,|b|)

公式表述

gcd(a,b)=gcd(b,a mod b)

证明：a可以表示成a = kb + r，则r = a mod b

假设d是a,b的一个公约数，则有

d|a, d|b，而r = a - kb，因此d|r

因此d是(b,a mod b)的公约数

假设d 是(b,a mod b)的公约数，则

d | b , d |r ，但是a = kb +r

因此d也是(a,b)的公约数

因此(a,b)和(b,a mod b)的公约数是一样的，其最大公约数也必然相等，得证

C++语言实现

 
         int  
         gcd( 
         int  
         a, 
         int  
         b){ 
        
         return  
         b?gcd(b,a%b):a; 
        
         }

扩展算法

对于不完全为 0 的非负整数 a，b，gcd（a，b）表示 a，b 的最大公约数，必然存在无数组整

数对 x，y ，使得 gcd（a，b）=ax+by。

c++语言实现

 
         int  
         gcd( 
         int  
         a, 
         int  
         b, 
         int  
         &x, 
         int  
         &y){ 
        
         if  
         (b==0){ 
        
         x=1,y=0; 
        
         return  
         a; 
        
         } 
        
         int  
         q=gcd(b,a%b,y,x); 
        
         y-=a/b*x; 
        
         return  
         q; 
        
         }

求解 x，y的方法的理解

设 a>b。

1，显然当 b=0，gcd（a，b）=a。此时 x=1，y=0；

2，a>b>0 时

设 ax1+ by1= gcd(a,b);

bx2+ (a mod b)y2= gcd(b,a mod b);

根据朴素的欧几里德原理有 gcd(a,b) = gcd(b,a mod b);

则:ax1+ by1= bx2+ (a mod b)y2;

即:ax1+ by1= bx2+ (a - [a / b] * b)y2=ay2+ bx2- [a / b] * by2;

也就是ax1+ by1 == ay2+ b(x2- [a / b] *y2);

根据恒等定理得：x1=y2; y1=x2- [a / b] *y2;

这样我们就得到了求解 x1,y1 的方法：x1，y1 的值基于 x2，y2.

上面的思想是以递归定义的，因为 gcd 不断的递归求解一定会有个时候 b=0，所以递归可以结束。

扩展欧几里德算法

扩展欧几里德算法是用来在已知a, b求解一组x，y使得ax+by = Gcd(a, b) =d(解一定存在，根据数论中的相关定理)。扩展欧几里德常用在求解模线性方程及方程组中。下面是一个使用C++的实现：

 
         int  
         exGcd( 
         int  
         a, 
         int  
         b, 
         int  
         &x, 
         int  
         &y) 
        
         { 
        
         if 
         (b==0) 
        
         { 
        
         x=1;y=0; 
        
         return  
         a; 
        
         } 
        
         int  
         r=exGcd(b,a%b,x,y); 
        
         int  
         t=x;x=y;y=t-a/b*y; 
        
         return  
         r; 
        
         }

把这个实现和Gcd的递归实现相比，发现多了下面的x,y 赋值过程，这就是扩展欧几里德算法的精髓。

可以这样思考:

对于a'=b,b'=a%b 而言，我们求得 x, y使得 a'x+b'y=Gcd(a',b')

由于b'=a%b=a-a/b*b (注：这里的/是程序设计语言中的除法)

那么可以得到:

a'x+b'y=Gcd(a',b') ===>

bx+(a - a / b * b)y = Gcd(a', b') = Gcd(a, b) ===>

ay +b(x - a / b*y) = Gcd(a, b)

因此对于a和b而言，他们的相对应的p，q分别是 y和(x-a/b*y)

使用扩展欧几里德算法解决不定方程的办法

对于不定整数方程pa+qb=c，若 c mod Gcd(a, b)=0,则该方程存在整数解，否则不存在整数解。

有种较为不严谨的方法证明，不过至少弥补了一点空白，望某些数论大师补充修改：

由于我们知道，存在一组x与y使得a*x+b*y=gcd(a,b)。

将等式两边同时乘以整数k，即a*x*k+b*y*k=gcd(a,b)*k。如果c mod gcd(a,b)=f，则0<=f<gcd(a,b)。

那么可以令c=gcd(a,b)*k+f。这样一来，就有a*x*k+b*y*k+f=c。

若f

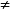0，由于f<gcd(a,b)<=a<=b（假设a<=b），所以不存在f=a*m（m为整数），也就不存在a*(x*k+m)+b*y*k=c。也就是说，不存在a*x+b*y=c的整数解x与y。

所以f=0，即只有当c mod gcd(a,b)=0时，a*x+b*y=c有正整数解。得证。

上面已经列出找一个整数解的方法，在找到p * a+q * b = Gcd(a, b)的一组解p0,q0后，p * a+q * b = Gcd(a, b)的其他整数解满足：

p = p0 + b/Gcd(a, b) * t

q = q0 - a/Gcd(a, b) * t(其中t为任意整数)

至于pa+qb=c的整数解，只需将p * a+q * b = Gcd(a, b)的每个解乘上 c/Gcd(a, b) 即可，但是所得解并不是该方程的所有解，找其所有解的方法如下：

在找到p * a+q * b = Gcd(a, b)的一组解p0,q0后，可以

得到p * a+q * b = c的一组解p1 = p0*(c/Gcd(a,b)),q1 = q0*(c/Gcd(a,b))，p * a+q * b = c的其他整数解满足：

p = p1 + b/Gcd(a, b) * t

q = q1 - a/Gcd(a, b) * t(其中t为任意整数)

p 、q就是p * a+q * b = c的所有整数解。

编程时 exgcd 更多用于求解“中国剩余定理”相关知识举个例子比如n除以5余2 除以13余3 那么n最小是多少，所有的n满足什么条件？

n（min)=42

n=42+k*65

欧几里德算法的扩展

扩展欧几里德算法不但能计算(a，b)的最大公约数，而且能计算a模b及b模a的乘法逆元，用C语言描述如下：

 
         int  
         gcd( 
         int  
         a, 
         int  
         b, 
         int  
         &ar, 
         int  
         &br) 
        
         { 
        
         int  
         x1,x2,x3; 
        
         int  
         y1,y2,y3; 
        
         int  
         t1,t2,t3; 
        
         if(0==a)//有一个数为0,就不存在乘法逆元 
        
         { 
        
         ar=0;br=0; 
        
         return b; 
        
         } 
        
         if(0==b) 
        
         { 
        
         ar=0;br=0; 
        
         return a; 
        
         } 
        
         x1=1;x2=0;x3=a; 
        
         y1=0;y2=1;y3=b; 
        
         int  
         nk; 
        
         for(t3=x3%y3;t3!=0;t3=x3%y3) 
        
         { 
        
         k=x3/y3; 
        
         t2=x2-k*y2;t1=x1-k*y1; 
        
         x1=y1;x2=y2;x3=y3; 
        
         y1=t1;y2=t2;y3=t3; 
        
         } 
        
         if(y3==1)//有乘法逆元 
        
         { 
        
         ar=(y2+b)%b;//对求出来负的乘法逆元进行处理，使之在模b的完全剩余集里 
        
         br=(y1+a)%a;//原来这里是错的 
        
         return 1; 
        
         } 
        
         else//公约数不为1,无乘法逆元 
        
         { 
        
         ar=0; 
        
         br=0; 
        
         return y3; 
        
         } 
        
         }