catia二维图坐标如何表示_你知道矩阵中二维，三维，四维，五维是如何表示的吗？...

现在假设我们有两个数字，我们可以表示二维空间中的任何点

现在假设我们有三个数字，我么 现在可以表示三维空间中的任何点

同样，如果我们有一组四个数字，我们可以代表四维空间中的任何一点

如果我们有一组五个数字，我们可以在五维空间中表示一个点

如果我们有无限的数字，我们可以用无限多个维度来表示空间中的一个点

无论我们有多少尺寸，每组数字代表空间中的一个点，可以被认为是一个箭头，我们称之为矢量，每个向量具有长度和方向

如果我们将向量乘以数字，向量的长度将会改变，但它的方向将保持不变

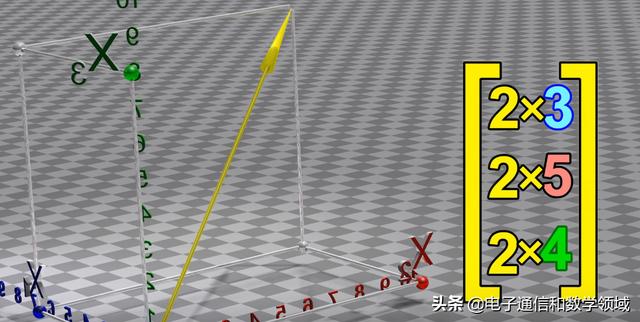
如果我们将两个向量相加，结果如图所示

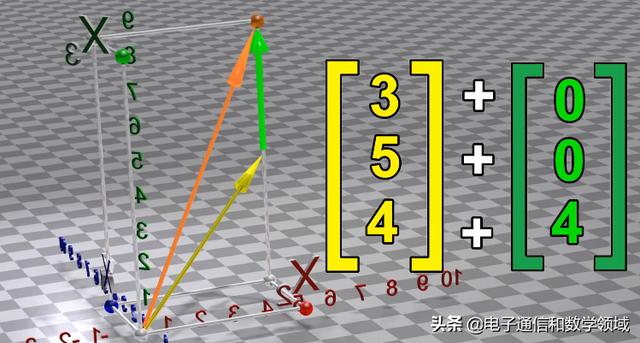
每个向量都可以被认为是，每个不同维度中指向的向量之和

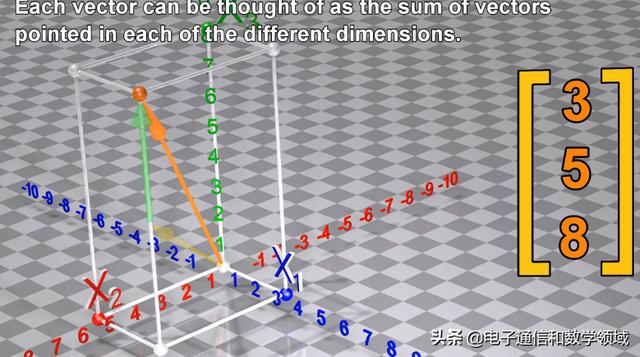
并且每个维度中指向的每个向量都可以被认为是向量长度为乘以数字

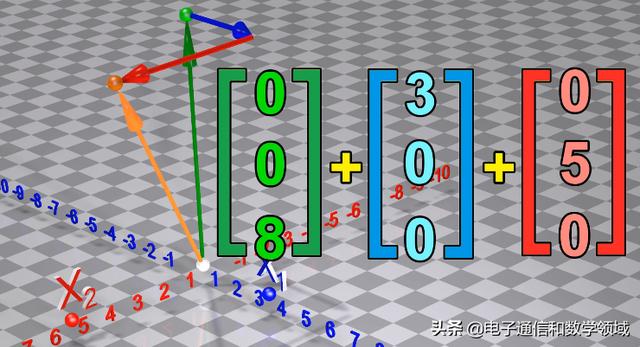
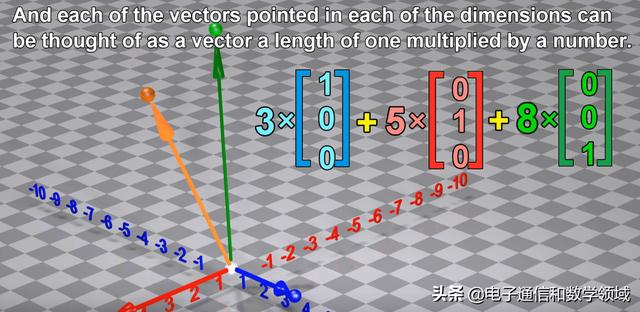
有许多转化可以应用于矢量，例如矢量可以围绕该轴在空间中旋转一定程度的度数

假设我们将此旋转应用于一组向量，然后我们将所有向量加在一起

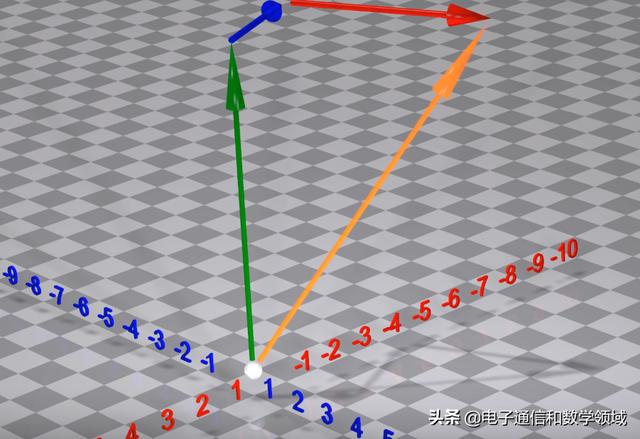
现在假设不是通过旋转矢量开始，我们首先将所有向量加在一起，然后我们旋转结果

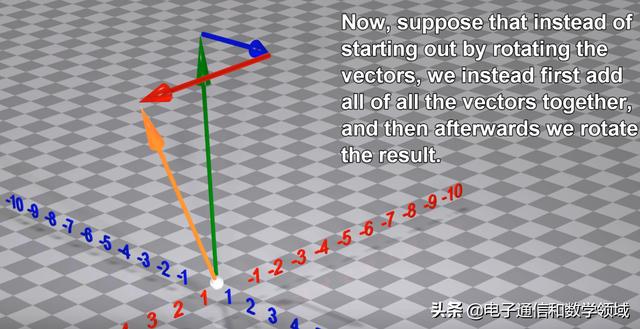
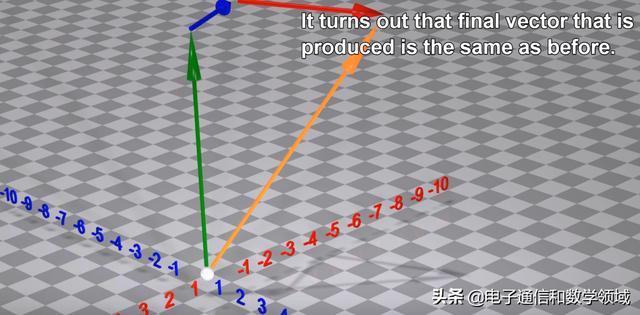
事实证明，生成的最终向量与之前相同