本文介绍了如何使用Dijkstra算法解决旅行商问题，以优化洒水车作业路径规划。针对不同数量的作业点，建立了线性规划模型，通过调整车辆路径来最小化总作业时间。内容包括问题描述、分析、数据预处理、模型建立与求解，以及最佳给水站的分配策略。模型考虑了不同车型的速度、作业时间和加水限制，旨在实现最短作业时间。
前言
最优化问题一直是国赛及各地区小比赛的热点问题。本题是线性规划、启发式算法的典型应用案例，结合地图类型数据，需要考虑的问题更加复杂。阅读本文前，建议读者掌握一定的编程基础、运筹学基础，并且配置好 python3 及 gurobi 环境。相关内容及其他案例可以参考以下文章：
Suranyi：gurobi 高效数学规划引擎 | python3 配置、使用及建模实例zhuanlan.zhihu.com
1 问题描述
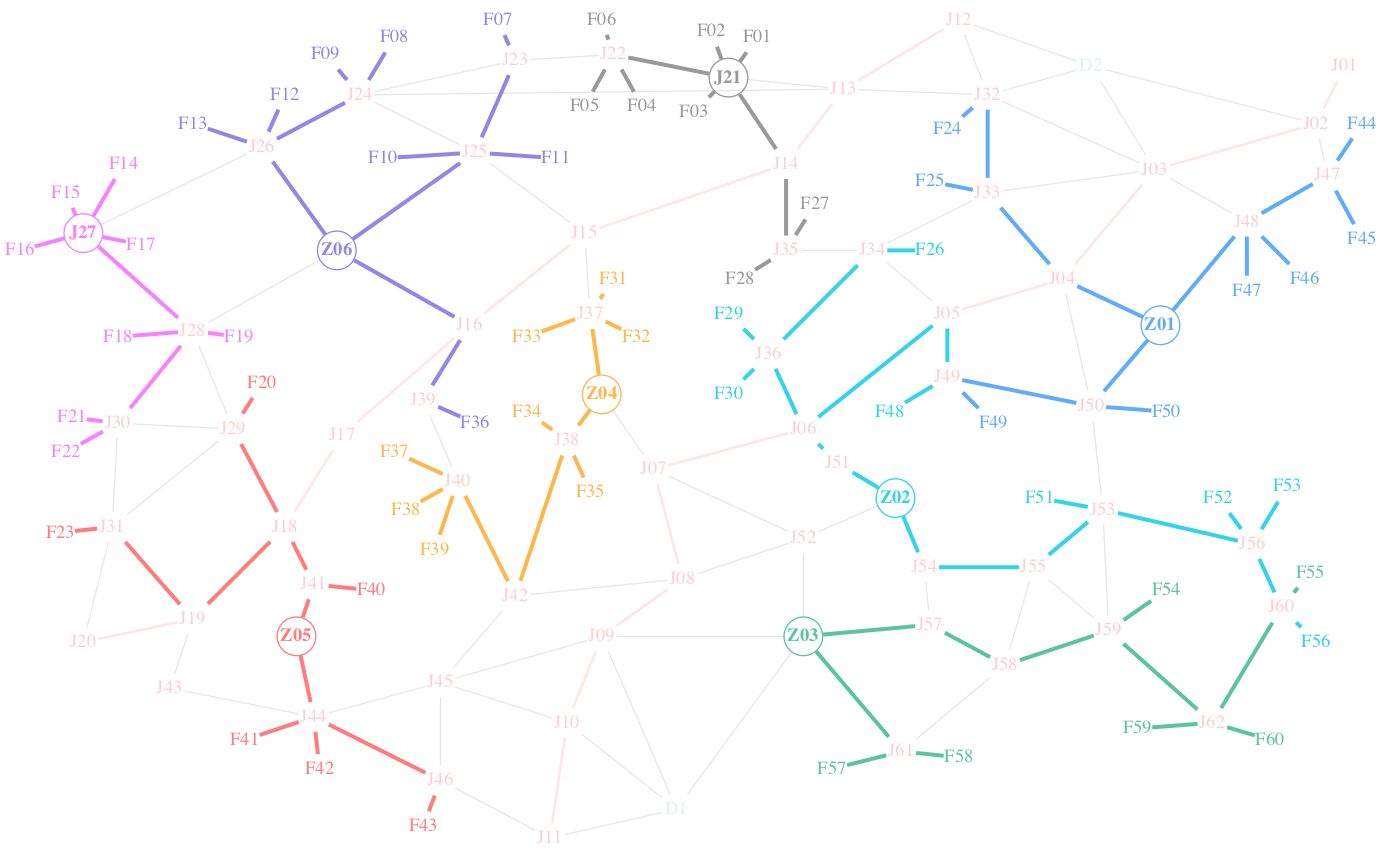
某城市共有绿化喷洒车20台，分为A、B两类。其中A、B类喷洒车分别有12辆、8辆，执行喷洒任务前平均部署在2个停靠点（D1，D2）。所属域内有6个给水站（Z01~ Z06）、60个喷洒作业点（F01~ F60），每一个喷洒作业点只需一台喷洒车进行一次作业。各给水站最多可以给八台喷洒车加水，不计加水时间。相关道路情况如图1所示（道路节点J01~J62），相关要素的坐标数据如“相关的要素名称及位置坐标数据”所示。图中红线主干道路，黑线是普通道路。A、B两类喷洒车在主干道路上的平均行驶速度分别是 60公里/小时、50公里/小时，在其他道路上的平均行驶速度分别是45公里/小时、30公里/小时。喷洒车装满水停靠在停靠点，接到喷洒任务后驶向喷洒作业点喷洒作业。一次喷洒作业A、B两类喷洒车分别需要用时20分钟、15分钟。每辆喷洒车完成一次喷洒任务后，需要到给水站加水再进行下次喷洒作业。
请建立数学模型研究下列任务相关问题：
(1) 任务一：每辆喷洒车只执行一次喷洒作业。请给出完成任务一的最短时间及相应的最优喷洒作业方案。
(2) 任务二：每辆喷洒车执行两次次喷洒作业。请给出完成任务二的最短时间及相应的最优喷洒作业方案。
(3) 任务三：完成所有60个喷洒作业点（F01~ F60）的喷洒任务。请给出完成任务三的最短时间及相应的最优喷洒作业方案。
(4) 如果在道路节点J01~J62中的某两个节点处分别增建一个给水站，请重新考虑问题(3)。并给出增建给水站的最佳位置。
2 问题分析
本题是路径调度方面的算法设计问题 (经典的多旅行商问题)，与 98 年国赛灾情巡视问题十分相似。由于其背景是真实世界中的交通网道，需要结合图论知识进行相关的数据处理工作 (如邻接关系表示、获取最短路径、分群等)。在建模中，满足分配路径的前提下尽可能符合某些背景下的 “高效”，是本题的重点。
附件提供了图中各要素的坐标，并以图片形式描述点之间的连接情况。在图论中，常用邻接矩阵表示图结构。例如：
因此，可以考虑先将图中的节点连接信息转化为 0-1 矩阵
- 在绘图时，根据附件中点的坐标可以标记出点的位置，再遍历矩阵中的元素，遇到
，则将点
与
相连。
- 在计算距离时，可以直接任意两点间的欧式距离，得到 “点 - 点 距离矩阵”。但这样的距离矩阵并不能真实反应两点之间的图距离。因此，在计算点
与点
的距离时，同时检查
是否等于1，如果不等于1，则将该处的距离修改为 inf，即两点不相连。
- 计算任意两点间的图距离，可以使用图论中的最短距离算法 （如Dijkstra、Floyd-Warshall算法）。题目中要求 “最短时间”，因此在给定两点
求这两点之间的最短路径。
求路径时，应该
获取邻接矩阵是必要的工作，最简单的操作就是人工标注法 (在excel中填写，或代码写两层 for 循环 + if 标注)。此处要注意，由于主道与支道车速不同，需要构造两份邻接矩阵。
import pandas as pd
point_name = pd.read_excel('../table/相关的要素名称及位置坐标数据.xls', index_col='要素编号').index
link_matrix = pd.DataFrame(0, index=point_name, columns=point_name)
for start_index, start in enumerate(point_name):
for end_index, end in enumerate(point_name[start_index + 1:]):
if input(f"L({start}-{end}) = ") == "1":
link_matrix.at[start, end] = link_matrix.at[end, start] = 1
link_matrix.to_excel("../table/边邻接矩阵.xlsx")由于题目中涉及不同车型速度、作业时间不同，而最终的优化目标是耗费时间尽可能短。因此需要将 “距离” 统一转化为使用的时间，作为边权值，构造 “A车 时间矩阵”，“B车 时间矩阵”。
考虑问题的“时间最短”，可以从以下两个角度出发：
- 总时间最短：
，它与平均用时最短是等价的；
- 最长用时最短：
。
“最长用时最短“反映该地区全部洒水任务完成所需的最长时间最小化，这两种优化目标都是符合题意的，考虑到第一种优化目标可能造成部分车用时过长的问题，因此这里选择第二种作为第一级优化目标，第一种作为第二级优化目标。（多目标优化问题）
对于第一问、第二问，20辆车在60个地点中选择20个地点、40个地点进行洒水作业，可以考虑转化为指派问题，使用线性规划类方法进行求解；也可以使用遗传算法进行求解。由于本题规模较小，使用线性规划进行求解。
对于第三问，由于没有强制规定每辆车都需要洒水3个地点。引申出两种假设：
- 洒水车没有洒水次数限制。即允许有的车前往作业点密集区执行多个洒水任务，有的车执行较少的洒水任务；
- 每辆车都执行3次洒水任务。
显然，如果使用第一种假设，动态仿真的思路更容易进行；第二种假设更适合遗传算法、线性规划等静态类模型。此外，由于补水站只能为 48 次作业任务补水，而完成 60 个点作业任务需要 60 次补水。因此认为最后 20 次任务完成后返回停靠点。
对于第四问，结合题意及实际背景，在给水站充足下，洒水车可以完成任务后停留在给水站，等待第二天 (下一轮) 作业任务。题目可以转为在
3 数据预处理
3.1 获取边接邻矩阵
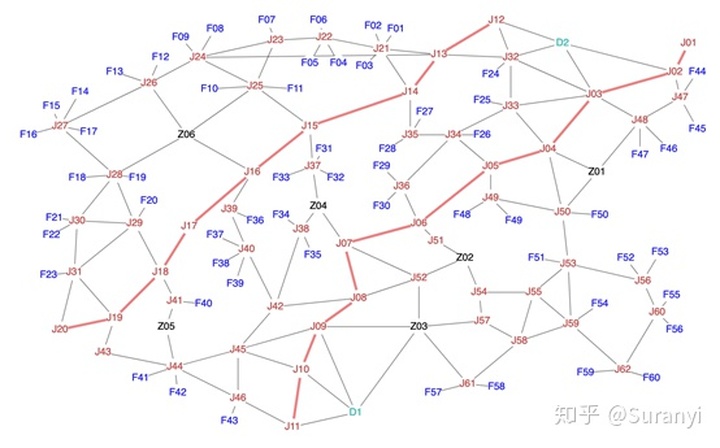
数据预处理的第一个工作是获取边邻接矩阵，我们采用基于人体 ATP 消耗的手工标记法进行 (找个学弟帮你画一下就行了！)。获得的标记数据分为邻接矩阵1、邻接矩阵2，前者是整个道路信息图，后者是主道图。两个矩阵按位进行异或运算即可得到支道图。
3.2 重构网络图
网络图 (节点图) 有多种绘制方式，Pyecharts、Matplotlib、python-igraph 都可以实现。这里我们使用 pygraphviz 进行绘图。快速入门及相关案例参考：
Suranyi：PyGraphviz (几何图形可视化工具) 简单入门zhuanlan.zhihu.com
import pandas as pd
import pygraphviz as pgv
link_matrix_1 = pd.read_excel("../table/边邻接矩阵1.xlsx", index_col=0)
link_matrix_2 = pd.read_excel("../table/边邻接矩阵2.xlsx", index_col=0)
point_location = pd.read_excel("../table/相关的要素名称及位置坐标数据.xls", index_col="要素编号")
# 绘图
G = pgv.AGraph(directed=False, concentrate=True)
# 添加节点
for point in point_location.index:
color = "#5bc49f" if point.startswith("D") else "blue" if point.startswith("F") else "red" if point.startswith("J") else "#000000"
G.add_node(point, shape="none", fontcolor=color, fixedsize=True, width=0.3, height=0.3,
pos=f"{0.06 * point_location.at[point, 'X坐标（单位：km）']},{0.06 * (point_location.at[point, 'Y坐标（单位：km）'])}!")
# 添加边
for start in point_location.index:
for end in point_location.index:
# 支道
if link_matrix_1.at[start, end] ^ link_matrix_2.at[start, end]:
G.add_edge(start, end)
# 主道
if link_matrix_2.at[start, end]:
G.add_edge(start, end, color="red", penwidth=2)
# 导出图形
G.layout()
G.draw("../image/地图.png")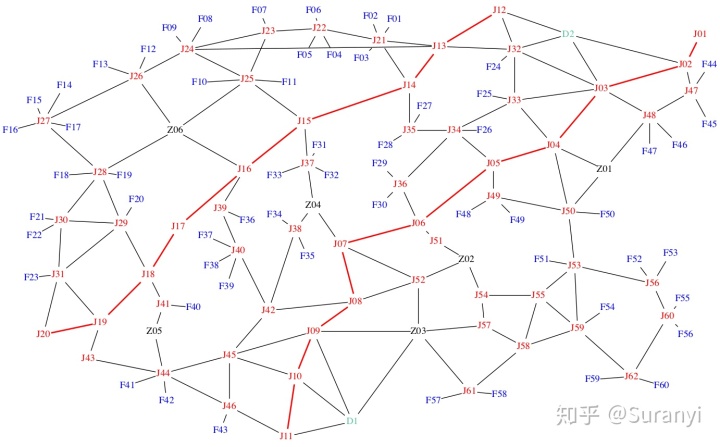
3.3 获取代价矩阵
图的最短路径可以使用 Dijkstra算法实现，算法细节可以自行搜索，本文基于 python-igraph，实现更便捷的 Jgraph 模块 (快速入门参考：社区网络分析学习笔记 —— 算法实现及 igraph 介绍，本文使用的 Jgraph 见文末附录)，调用该工具实现。将得到的A车代价矩阵、B车代价矩阵、距离矩阵分别记为
import pandas as pd
from Jgraph import Jgraph
# %% 1.导入数据
link_matrix_1 = pd.read_excel('../table/边邻接矩阵1.xlsx', index_col=0) # 全网络图数据
link_matrix_2 = pd.read_excel('../table/边邻接矩阵2.xlsx', index_col=0) # 主干道网络图数据
point_location = pd.read_excel('../table/相关的要素名称及位置坐标数据.xls', index_col='要素编号')
point_name = point_location.index
# %% 2. 距离矩阵
distance = pd.DataFrame(0.0, index=point_name, columns=point_name)
for start in point_name:
for end in point_name:
x1, y1 = point_location.at[start, 'X坐标（单位：km）'], point_location.at[start, 'Y坐标（单位：km）']
x2, y2 = point_location.at[end, 'X坐标（单位：km）'], point_location.at[end, 'Y坐标（单位：km）']
distance.at[start, end] = ((x1 - x2) ** 2 + (y1 - y2) ** 2) ** (1 / 2)
A_matrix_1 = distance / 60 # A 车主干道时间
A_matrix_2 = distance / 45 # A 车支干道时间
B_matrix_1 = distance / 50 # B 车主干道时间
B_matrix_2 = distance / 30 # B 车支干道时间
# %% 3.最短路径矩阵
def shortest_matrix(matrix_1, matrix_2):
nodes = [{
"name": i} for i in matrix_1.index]
links = []
for start_index, start in enumerate(point_name):
for end in point_name[start_index + 1:]:
if link_matrix_1.at[start, end] ^ link_matrix_2.at[start, end]:
links.append({
"source": start, "target": end, "value": matrix_1.at[start, end]})
if link_matrix_2.at[start, end]:
links.append({
"source": start, "target": end, "value": matrix_2.at[start, end]})
# 生成 Jgraph 图，调用最短路径算法
graph = Jgraph(nodes, links)
paths = graph.shortest_paths(point_name, point_name, 'mult
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
