三角函数专题【高阶辅导】

Ⅰ、三角函数和解三角形知识结构图

Ⅱ、主要的知识点和相关题型

1、角的集合表示：角的终边在直线上，角的终边在射线上，在扇形内，在对顶扇形内，象限角，象限界角，区间角等。

2、弧长与扇形面积公式及其应用，

方法：均值不等式（两种形式）；二次函数（变量集中）

3、已知角\(\alpha\)的象限，判断\(\cfrac{\alpha}{n}\)的象限 方法：计算法， 八卦图法

4、考察三角函数的定义，单位圆定义是特例。更一般的定义是利用坐标之比定义。和圆的参数方程形式有关联。

5、三角函数值符号的判断

6、解三角不等式 法1：三角函数线的应用。 法2、三角函数图像

7、同角三角函数基本关系的应用 齐次式， \(\sin\alpha+\cos\alpha\)， \(\sin\alpha-\cos\alpha\)， \(\sin\alpha\cdot \cos\alpha\)，知一求二

8、【三角函数图像和性质，\(y=\sin x\)，\(y=\cos x\)等模板函数】三角函数的定义域\(\Longrightarrow\)解三角不等式，

三角函数的值域 直接法，化一法，换元法

9、求三角函数的单调区间 代换法 图像法

10、求三角函数的奇偶、周期、对称性， 整体法+模板法

11、作函数\(y=A\sin(\omega x+\phi)+k\)的图像 五点法 快速作图法

12、函数\(y=A\sin(\omega x+\phi)+k\)的图像变换 实质：替换

13、由图像或文字确定函数\(y=A\sin(\omega x+\phi)+k\)的四个参数，待定系数法 +具体确定公式

14、函数\(y=A\sin(\omega x+\phi)+k\)的图像和性质 以\(y=\sin x\)为模板，各种性质

15、函数\(y=A\sin(\omega x+\phi)+k\)的模型应用 三角函数应用题目

16、三角函数式的化简

方法：异名化同名，异角化同角，异次化同次，弦切互化，1的代换，通分，约分，特殊值特殊角互化

• \(1+\sin\theta+\cos\theta=\sin\theta+(1+\cos\theta)=2\sin\cfrac{\theta}{2}\cos\cfrac{\theta}{2}+2\cos^2\cfrac{\theta}{2}=2\cos\cfrac{\theta}{2}(\sin\cfrac{\theta}{2}+\cos\cfrac{\theta}{2})\)

• \(1+\sin\theta-\cos\theta=\sin\theta+(1-\cos\theta)=2\sin\cfrac{\theta}{2}\cos\cfrac{\theta}{2}+2\sin^2\cfrac{\theta}{2}=2\sin\cfrac{\theta}{2}(\sin\cfrac{\theta}{2}+\cos\cfrac{\theta}{2})\)

17、三角函数的求值

类型一：给角求值 \(\Longrightarrow\)化简

类型二：给值求值 方法：从观察已知角入手，给一个角求一个角，利用余、补、半、倍、特等建立关系；给两个角求一个角，利用和、差建立关系

类型三：给值求角\(\Longrightarrow\)转化为给值求值+角的范围(注意：所求角的三角函数的确定有原则，角的范围可能需要结合题目压缩)

18、简单的三角恒等变换

19、正弦定理和余弦定理的各种形式记忆、公式的内容及其证明，

20、应用正弦定理和余弦定理解三角形 理解掌握她们各自解决的两种类型。

21、判断三角形的形状。 （三角形内的诱导公式） 及其P61充要条件

方法：角化边，边化角。约分时要注意在三角形中\(sinA\ne 0\)，但是\(cosA=0\)是可能的，要注意排除。 还有 \(sin2A=sin2B\)的结果的留意。

22、与三角形的面积有关的问题。

23、解三角形应用。理解各种概念 测量距离、高度、角度和平面几何中的应用

Ⅲ、章节的重点和难点

1、关于\(\sin\theta、\cos\theta\)的齐次式变量集中

①一次齐次式， 如\(a\sin\theta+b\cos\theta\)，常借助分式形式考察\(\cfrac{a\sin\theta+b\cos\theta}{c\sin\theta+d\cos\theta}\) (\(a,b,c,d\)为常数)

②二次齐次式， 如\(a\sin2\theta+b\sin\theta\cos\theta+c\cos2\theta\)，\(\sin2\theta\)， \(\cos2\theta\)，\(1+\sin2\theta\)， \(2-\cos2\theta\)，\(3\sin2\theta-2\cos2\theta\)， 等等

思路：可以恢复分母\(1=\sin^2\theta+\cos^2\theta\)，变成分子分母都是二次齐次式，

③四次齐次式，如已知\(tan\theta=3\)，求值\(sin^4\theta-3sin\theta\cdot cos^3\theta+cos^4\theta\)；

思路：恢复分母\(1=1^2=(\sin^2\theta+\cos^2\theta)^2\)，变成分子分母都是四次齐次式，

分析：原式=\(\cfrac{sin^4\theta-3sin\theta\cdot cos^3\theta+cos^4\theta}{(\sin^2\theta+\cos^2\theta)^2}\)

\(=\cfrac{sin^4\theta-3sin\theta\cdot cos^3\theta+cos^4\theta}{\sin^4\theta+\cos^4\theta+2sin^2\theta\cdot cos^2\theta}\)，给分子分母同时除以\(cos^4\theta\)得到，

\(=\cfrac{tan^4\theta-3tan\theta+1}{tan^4\theta+2tan^2\theta+1}\)，然后代值计算。

④一次齐次式变为二次齐次式的思路：两边平方+恢复分母1，

2、三角函数的求值三角函数求值

类型一：给角求值 \(\Longrightarrow\)化简

类型二：给值求值 方法：从观察已知角入手，给一个角求一个角，利用余、补、半、倍、特等建立关系；给两个角求一个角，利用和、差建立关系

类型三：给值求角\(\Longrightarrow\)转化为给值求值+角的范围(注意：所求角的三角函数的确定有原则，角的范围可能需要结合题目压缩)

3、解三角形

4、三角函数和解三角形的交汇处的题型

这类题目往往会设置第一问求一个角（如\(A\)）,第二问已知边\(a\)（注意对角和对边的关系），接下来可以考查的方向有

①再已知\(S_△\)，求解\(b+c\)的取值范围； 或者已知\(b+c\)求\(S_△\)的取值范围。

②求解\(msinB+nsinC\)的取值范围(\(m、n\)是实数)

③求解\(msinB\cdot nsinC\)的取值范围(\(m、n\)是实数)

④求解\(S_△=\cfrac{1}{2}bcsinA\)的取值范围

⑤求解周长的取值范围 \(l=a+b+c\)

⑥求解类似周长的取值范围 \(l=2a+3b-c\)

⑦难点：自变量的取值范围，已知三角形和锐角三角形时，自变量的范围是不一样的。

Ⅳ、本章节中的常用公式总结提炼

①数学常识三角函数内容

②三角函数知识点三角函数识记

典型例题

例1已知函数\(f(x)=2sinx\cdot cosx+2\sqrt{3}\cdot cos^2x-\sqrt{3}+1\)，

①将函数转化为正弦型；②求周期；③求值域；④求单调区间；⑤求对称性；⑥求奇偶性；

变形方向：正弦型(或余弦型)；变形公式：逆用二倍角的正弦、余弦公式和辅助角公式；

\(f(x)=sin2x+\sqrt{3}(1+cos2x)-\sqrt{3}+1\)

\(=sin2x+\sqrt{3}cos2x+1\)

\(=2sin(2x+\cfrac{\pi}{3})+1\)

①求周期；

由\(T=\cfrac{2\pi}{2}\)，得到\(T=\pi\)

②求值域\((x\in R 或 x\in [-\cfrac{\pi}{3}，\cfrac{\pi}{4}])\)；最值(和最值点)；

若\(x\in R\)，则

当\(sin(2x+\cfrac{\pi}{3})=1\)时，即\(2x+\cfrac{\pi}{3}=2k\pi+\cfrac{\pi}{2}(k\in Z)\)，即\(x=k\pi+\cfrac{\pi}{12}(k\in Z)\)时，\(f(x)_{max}=2\times1+1=3\)；

当\(sin(2x+\cfrac{\pi}{3})=-1\)时，即\(2x+\cfrac{\pi}{3}=2k\pi-\cfrac{\pi}{2}(k\in Z)\)，即\(x=k\pi-\cfrac{5\pi}{12}(k\in Z)\)时，\(f(x)_{max}=2\times(-1)+1=-1\)；

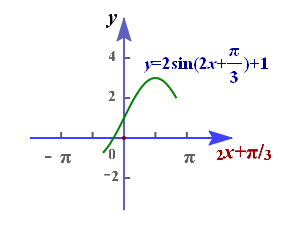
若\(x\in [-\cfrac{\pi}{3}，\cfrac{\pi}{4}]\)，则可得

\(-\cfrac{2\pi}{3}\leq 2x\leq \cfrac{\pi}{2}\)，则\(-\cfrac{\pi}{3}\leq 2x+\cfrac{\pi}{3}\leq \cfrac{5\pi}{6}\)，

故当\(2x+\cfrac{\pi}{3}=-\cfrac{\pi}{3}\)，即\(x=-\cfrac{\pi}{3}\)时，\(f(x)_{min}=f(-\cfrac{\pi}{3})=2\times (-\cfrac{\sqrt{3}}{2})+1=-\sqrt{3}+1\)；

故当\(2x+\cfrac{\pi}{3}=\cfrac{\pi}{2}\)，即\(x=\cfrac{\pi}{12}\)时，\(f(x)_{max}=f(\cfrac{\pi}{12})=2\times 1+1=3\)；

③求单调区间\(\left(x\in R 或x\in [-\cfrac{\pi}{4}，\cfrac{\pi}{2}]\right)\)(具体解法参见例2的法1和法2)

④求函数\(f(x)\)对称轴方程和对称中心坐标；

令\(2x+\cfrac{\pi}{3}=k\pi+\cfrac{\pi}{2}(k\in Z)\)，得到\(f(x)\)对称轴方程为\(x=\cfrac{k\pi}{2}+\cfrac{\pi}{12}(k\in Z)\)；

令\(2x+\cfrac{\pi}{3}=k\pi(k\in Z)\)，得到\(f(x)\)的对称中心坐标为\((\cfrac{k\pi}{2}-\cfrac{\pi}{6}，1)(k\in Z)\)

⑤求奇偶性\(\left(奇函数利用f(0)=0；偶函数利用f(0)=f(x)_{max}或f(x)_{min}\right)\)

比如，函数\(g(x)=2sin(2x+\phi+\cfrac{\pi}{3})(\phi\in (0，\pi))\)是偶函数，求\(\phi\)的值。

分析：由于函数\(g(x)\)是偶函数，则在\(x=0\)处必然取到最值，

故有\(2\times 0+\phi+\cfrac{\pi}{3}=k\pi+\cfrac{\pi}{2}(k\in Z)\)，

则\(\phi=k\pi+\cfrac{\pi}{6}(k\in Z)\)

令\(k=0\)，则\(\phi=\cfrac{\pi}{6}\in (0，\pi)\)，满足题意，故所求\(\phi=\cfrac{\pi}{6}\)时，函数\(g(x)\)是偶函数。

例1(2016\(\cdot\)天津高考改编) 已知函数\(f(x)=4tanx\cdot sin(\cfrac{\pi}{2}-x)\cdot cos(x-\cfrac{\pi}{3})-\sqrt{3}\)，试讨论\(f(x)\)在区间\([-\cfrac{\pi}{4}，\cfrac{\pi}{4}]\)上的单调性。

解析：先将所给函数化简为正弦型或者余弦型，

\(f(x)=4tanx\cdot cosx(cosx\cdot \cfrac{1}{2}+sinx\cdot \cfrac{\sqrt{3}}{2})-\sqrt{3}\)

\(=4sinx(cosx\cdot \cfrac{1}{2}+sinx\cdot \cfrac{\sqrt{3}}{2})-\sqrt{3}=2sinxcosx+2\sqrt{3}sin^2x-\sqrt{3}\)

\(=sin2x+\sqrt{3}(1-cos2x)-\sqrt{3}=sin2x-\sqrt{3}cos2x\)

\(=2sin(2x-\cfrac{\pi}{3})\)

法1：先求解函数在\(x\in R\)上的单调区间，

令\(2k\pi-\cfrac{\pi}{2}\leq 2x-\cfrac{\pi}{3}\leq 2k\pi+\cfrac{\pi}{2}(k\in Z)\)，

得到单调递增区间为\([k\pi-\cfrac{\pi}{12}，k\pi+\cfrac{5\pi}{12}](k\in Z)\)，

又因为\(x\in [-\cfrac{\pi}{4}，\cfrac{\pi}{4}]\)

然后给\(k\)赋值，令\(k=0\)，

得到函数在区间\([-\cfrac{\pi}{12}，\cfrac{\pi}{4}]\)上单调递增，在区间\([-\cfrac{\pi}{4}，-\cfrac{\pi}{12}]\)上单调递减。

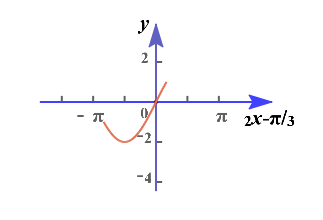
法2：由\(-\cfrac{\pi}{4}\leq x\leq \cfrac{\pi}{4}\)，求得\(-\cfrac{5\pi}{6}\leq 2x-\cfrac{\pi}{3}\leq \cfrac{\pi}{6}\)，

结合横轴为\(2x-\cfrac{\pi}{3}\)的图像可知，

当\(-\cfrac{5\pi}{6}\leq 2x-\cfrac{\pi}{3}\leq -\cfrac{\pi}{2}\)时，求得函数在区间\([-\cfrac{\pi}{4}，-\cfrac{\pi}{12}]\)单调递减；

当\(-\cfrac{\pi}{2}\leq 2x-\cfrac{\pi}{3}\leq \cfrac{\pi}{6}\)时，求得函数在区间\([-\cfrac{\pi}{12}，\cfrac{\pi}{4}]\)单调递增；

静雅凤中$\;\cdot\;$三角函数和解三角形专题$\;\cdot\;$针对性训练题 (2016宝鸡市第二次质量检测第17题)考查目的：三角函数和解三角形的综合应用 在$\Delta ABC$中，已知$sin^2A+sin^2B+sinAsinB=sin^2C$，其中角$A、B、C$的对边分别为$a、b、c$， (1).求角$C$的大小。 (2).求$\cfrac{a+b}{c}$的取值范围。

---

分析：(1)角化边，由$\cfrac{a}{2R}=sinA，\cfrac{b}{2R}=sinB，\cfrac{c}{2R}=sinC$ 得到$a^2+b^2+ab=c^2$，即$a^2+b^2-c^2=-ab$， 故由余弦定理得到$cosC=\cfrac{a^2+b^2-c^2}{2ab}=-\cfrac{1}{2}$， 又$C\in (0，\pi)$，故$C=\cfrac{2\pi}{3}$。 (2)由(1)可知，$A+B=\cfrac{\pi}{3}$，即$A=\cfrac{\pi}{3}-B$ 边化角，由$a=2RsinA，b=2RsinB，c=2RsinC$ $\cfrac{a+b}{c}=\cfrac{sinA+sinB}{sinC}=\cfrac{2\sqrt{3}}{3}(sinA+sinB)$ $=\cfrac{2\sqrt{3}}{3}[sin(\cfrac{\pi}{3}-B)+sinB]$ $=\cfrac{2\sqrt{3}}{3}[\cfrac{\sqrt{3}}{2}cosB-\cfrac{1}{2}sinB+sinB]$ $=\cfrac{2\sqrt{3}}{3}(\cfrac{1}{2}sinB+\cfrac{\sqrt{3}}{2}cosB)$ $=\cfrac{2\sqrt{3}}{3}sin(B+\cfrac{\pi}{3})$， 计算角B的取值范围由 $\begin{cases}B>0\\ \cfrac{\pi}{3}-B>0\end{cases}$ $B\in (0,\cfrac{\pi}{3})$ $B+\cfrac{\pi}{3}\in (\cfrac{\pi}{3},\cfrac{2\pi}{3})$ $\cfrac{\sqrt{3}}{2} < sin(B+\cfrac{\pi}{3}) \leq 1 $ $1 即$\cfrac{a+b}{c}$的取值范围为$(1，\cfrac{2\sqrt{3}}{3}]$。

静雅凤中$\;\cdot\;$三角函数和解三角形专题$\;\cdot\;$针对性训练题 考查目的：三角函数的变换；题型：三角函数的求值，给值求值 已知$\alpha$为第二象限角，$sin(\alpha+\cfrac{\pi}{4})=\cfrac{\sqrt{2}}{10}$，则$tan\cfrac{\alpha}{2}$的值为多少？

---

法1：变形得到$\cfrac{\sqrt{2}}{2}(sin\alpha+cos\alpha)=\cfrac{\sqrt{2}}{10}$，解得$sin\alpha+cos\alpha=\cfrac{1}{5}$， 又因为$\alpha$为第二象限角，再结合勾股数可得$sin\alpha=\cfrac{4}{5}，cos\alpha=-\cfrac{3}{5}$；故$tan\alpha=-\cfrac{4}{3}$， 又由八卦图法可知$\cfrac{\alpha}{2}$在第一、三象限，故$tan\cfrac{\alpha}{2}>0$， 再由$tan\alpha=-\cfrac{4}{3}=\cfrac{2tan\cfrac{\alpha}{2}}{1-(tan\cfrac{\alpha}{2})^2}$， 解方程得到$tan\cfrac{\alpha}{2}=2$； 法2：同上法，得到$sin\alpha=\cfrac{4}{5}，cos\alpha=-\cfrac{3}{5}$； $tan\cfrac{\alpha}{2}=\cfrac{sin\cfrac{\alpha}{2}}{cos\cfrac{\alpha}{2}}=\cfrac{2sin\cfrac{\alpha}{2}cos\cfrac{\alpha}{2}}{2cos\cfrac{\alpha}{2}cos\cfrac{\alpha}{2}}$ $=\cfrac{sin\alpha}{1+cos\alpha}=\cfrac{\cfrac{4}{5}}{1-\cfrac{3}{5}}=2$；

静雅凤中$\;\cdot\;$三角函数和解三角形专题$\;\cdot\;$针对性训练题 考查目的：三角函数的变换，三角函数的性质 已知$f(x)=2Acos^2(\omega x+\phi)(A>0,\omega>0,0 $A．[k\pi-\cfrac{2\pi}{3} ，k\pi-\cfrac{\pi}{6}](k\in Z)$；$\hspace{2cm}$ $B．[k\pi-\cfrac{\pi}{6} ，k\pi+\cfrac{\pi}{3}](k\in Z)$; $C．[k\pi-\cfrac{5\pi}{12} ，k\pi+\cfrac{\pi}{12}](k\in Z)$；$\hspace{2cm}$ $D．[k\pi+\cfrac{\pi}{12} ，k\pi+\cfrac{7\pi}{12}](k\in Z)$;

---

分析：这类题目一般需要先将$f(x)$转化为正弦型或者余弦型，再利用给定的条件分别求$\omega$和$\phi$， 由$f(x)=2Acos^2(\omega x+\phi)=A[cos2(\omega x+\phi)+1]=Acos(2\omega x+2\phi)$， 故其周期为$T=\cfrac{2\pi}{2\omega}=\cfrac{\pi}{\omega}$， 又由题目可知$\cfrac{T}{4}=\cfrac{\pi}{3}-\cfrac{\pi}{12}=\cfrac{\pi}{4}$，则$T=\pi=\cfrac{\pi}{\omega}$， 故$\omega=1$，则函数简化为$f(x)=Acos(2x+2\phi)$， 再利用直线$x=\cfrac{\pi}{3}$是函数$f(x)$图象上的一条对称轴， 故$2\times \cfrac{\pi}{3}+2\phi=k\pi,(k\in Z)$, 解得$\phi=\cfrac{k\pi}{2}-\cfrac{\pi}{3}$，令$k=1$，则$\phi=\cfrac{\pi}{6}\in (0,\cfrac{\pi}{2})$， 满足题意，故$f(x)=Acos(2x+2\phi)=Acos(2x+\cfrac{\pi}{3})$. 令$2k\pi-\pi\leq 2x+\cfrac{\pi}{3}\leq 2k\pi(k\in Z)$， 解得$k\pi-\cfrac{2\pi}{3}\leq x \leq k\pi-\cfrac{\pi}{6}$， 即单调递增区间为$A．[k\pi-\cfrac{2\pi}{3} ，k\pi-\cfrac{\pi}{6}](k\in Z)$;

静雅凤中$\;\cdot\;$三角函数和解三角形专题$\;\cdot\;$针对性训练题 考查目的：三角函数的变换技巧(连比形式，巧设比例因子) 在$\Delta ABC$中，$tanA:tanB:tanC=1:2:3$，求$\cfrac{AC}{AB}$的值；

---

分析：(巧设比例因子)设$tanA=k,tanB=2k,tanC=3k,(k>0)$, 则由$tanA\times tanB\times tanC=tanA+tanB+tanC$可知， $6k=6k^3$,解得$k=1$.则有$tanA=1,tanB=2,tanC=3$, 再设比例因子，比如设$sinB=2m,cosB=m,(m>0)$,由平方关系可得，$5m^2=1,m=\cfrac{1}{\sqrt{5}}$, 故$sinB=\cfrac{2}{\sqrt{5}},sinC=\cfrac{3}{\sqrt{10}}$,则$\cfrac{AC}{AB}=\cfrac{sinB}{sinC}=\cfrac{\cfrac{2}{\sqrt{5}}}{\cfrac{3}{\sqrt{10}}}=\cfrac{2\sqrt{2}}{3}$.

静雅凤中$\;\cdot\;$三角函数和解三角形专题$\;\cdot\;$针对性训练题 (三角函数图像性质和解三角形结合)(2017•福州模拟) 在$\Delta ABC$中，角$A，B，C$的对边分别为$a，b，c$，满足$(2b-c)\cdot cosA=a\cdot cosC$。　 (1)求角$A$的大小；(考查角度：解三角形) (2)若$a=3$，求$\Delta ABC$的周长的最大值。(考查角度：三角函数图像性质)

---

分析： (1)由$(2b-c)\cdot cosA=a\cdot cosC$及正弦定理， 得$(2sinB-sinC)cosA=sinAcosC$， 所以$2sinBcosA=sinCcosA+sinAcosC$， 所以$2sinBcosA=sin(C+A)=sinB$， 因为$B\in (0，π)$，所以$sinB\neq 0$， 因为$A\in (0，π)$，$cosA=\cfrac{1}{2}$，所以$A=\cfrac{\pi}{3} $。 (2)由(1)得$A=\cfrac{\pi}{3} $， 由正弦定理得$\cfrac{b}{sinB}=\cfrac{c}{sinC} =\cfrac{a}{sinA} =\cfrac{3}{\frac{\sqrt{3}}{2}} =2\sqrt{3}$， 所以$b=2\sqrt{3}\cdot sinB$； $c=2\sqrt{3}\cdot sinC$， $\Delta ABC$的周长：$l=3+2\sqrt{3}\cdot sinB+2\sqrt{3}\cdot sinC$ $=3+2\sqrt{3}\cdot sinB+2\sqrt{3}\cdot sin(\cfrac{2\pi}{3}-B)$ $=3+2\sqrt{3}\cdot sinB+2\sqrt{3}\cdot (\cfrac{\sqrt{3}}{2}cosB+\cfrac{1}{2}sinB)$ $=3+3\sqrt{3}sinB+3cosB=3+6sin(B+\cfrac{\pi}{6})$ 因为$B\in(0，\cfrac{2\pi}{3})$，所以当$B=\cfrac{\pi}{3}$ 时，$\Delta ABC$的周长取得最大值，最大值为9。 反思总结：三角函数和解三角形的交汇处的题型 这类题目往往会设置第一问求一个角（如$A$）,第二问已知边$a$（注意对角和对边的关系），接下来可以考查的方向有 ①再已知$S_△$，求解$b+c$的取值范围； 或者已知$b+c$求$S_△$的取值范围。 ②求解$msinB+nsinC$的取值范围($m、n$是实数) ③求解$msinB\cdot nsinC$的取值范围($m、n$是实数) ④求解$S_△=\cfrac{1}{2}bcsinA$的取值范围 ⑤求解周长的取值范围 $l=a+b+c$ ⑥求解类似周长的取值范围 $l=2a+3b-c$ ⑦难点：自变量的取值范围，已知三角形和锐角三角形时，自变量的范围是不一样的。

静雅凤中$\;\cdot\;$三角函数和解三角形专题$\;\cdot\;$针对性训练题 (2017高考真题 理科全国卷2的第17题) $\Delta ABC$ 的内角A，B，C的对边分别是$a，b，c$，已知$sin(A+C)=8sin^2\cfrac{B}{2}$。 (1)求$cosB$. (2)若$a+c=6$，$S_{\Delta ABC}=2$，求$b$.

---

分析：$sin(A+C)=sinB=8\cdot \cfrac{1-cosB}{2}$，得到$sinB=4(1-cosB)$， 即$\sqrt{1-cos^2B}=4(1-cosB)$，平方得到$17cos^2B-32cosB+15=0$。 由十字相乘法得到 $(17cosB-15)(cosB-1)=0$，得到$cosB=\cfrac{15}{17}$或$cosB=1(舍去)$， 故$cosB=\cfrac{15}{17}$； (2)若$a+c=6$，$S_{\Delta ABC}=2$，求$b$. 分析：由$cosB=\cfrac{15}{17}$得到$sinB=\cfrac{8}{17}$， 由$S_{\Delta ABC}=\cfrac{1}{2}acsinB=2$得到，$ac=\cfrac{17}{2}$， 故$b^2=a^2+c^2-2accosB=(a+c)^2-2ac-2accosB=6^2-2\cdot \cfrac{17}{2}-2\cdot \cfrac{17}{2}\cdot\cfrac{15}{17}=4$， 故$b=2$。

静雅凤中$\;\cdot\;$三角函数和解三角形专题$\;\cdot\;$针对性训练题 (2017高考真题 文科全国卷2的第16题) $\Delta ABC的内角A，B，C的对边分别是a，b，c$，若$2bcosB=acosC+ccosA$，则$B$=________.

---

法1：角化边，得到$2b\cdot \cfrac{a^2+c^2-b^2}{2ac}=a\cdot \cfrac{a^2+b^2-c^2}{2ab}+c\cdot \cfrac{b^2+c^2-a^2}{2bc}$ 两边同乘以$abc$，约掉分母，化简整理为$a^2+c^2-b^2=ac$， 故$cosB=\cfrac{a^2+c^2-b^2}{2ac}=\cfrac{1}{2}$，又$b\in (0，\pi)$，则$B=\cfrac{\pi}{3}$。 法2：边化角，由已知得到$2sinBcosB=sinAcosC+cosAsinC=sin(A+C)=sinB$，故得到$cosB=\cfrac{1}{2}$，又$B\in (0，\pi)$，则$B=\cfrac{\pi}{3}$。

静雅凤中$\;\cdot\;$三角函数和解三角形专题$\;\cdot\;$针对性训练题 (2017高考真题 文科全国卷2的第13题) 函数$f(x)=2cosx+sinx$的最大值为_______。

---

分析：$f(x)=\sqrt{5}sin(x+\phi)(tan\phi=2)$，故$f(x)_{max}=\sqrt{5}$。

静雅凤中$\;\cdot\;$三角函数和解三角形专题$\;\cdot\;$针对性训练题 (2017高考真题 理科全国卷2的第14题) 函数$f(x)=sin^2x+\sqrt{3}cosx-\cfrac{3}{4}(x\in[0，\cfrac{\pi}{2}])$的最大值为_______。

---

分析：由于$x\in[0，\cfrac{\pi}{2}]$，则$cosx\in [0，1]$， 令$cosx=t\in [0，1]$，$f(x)=1-cos^2x+\sqrt{3}cosx-\cfrac{3}{4}=1-t^2+\sqrt{3}t-\cfrac{3}{4}=-(t-\cfrac{\sqrt{3}}{2})^2+1=g(t)$， 故当$t=\cfrac{\sqrt{3}}{2}$时，$g(t)_{max}=f(x)_{max}=1$。 反思总结：这类题目常有两个考查方向：①转化为正弦型求最值；②转化为二次型求最值。

静雅凤中$\;\cdot\;$三角函数和解三角形专题$\;\cdot\;$针对性训练题 (2017高考真题 文科全国卷1的第11题) $\Delta ABC的内角A，B，C的对边分别是a，b，c$，已知$sinB+sinA\cdot (sinC-cosC)=0，a=2，c=\sqrt{2}$，则$C$=________。

---

分析：由于$sinB=sin(A+C)=sinAcosC+cosAsinC$，则有$sinAcosC+cosAsinC+sinAsinC-sinAcosC=0$， 即$cosAsinC+sinAsinC=0$，又因为$sinC\neq 0$，故得到$sinA+cosA=0$，即$tanA=-1$ ，即$A=\cfrac{3\pi}{4}$， 由正弦定理$\cfrac{a}{sinA}=\cfrac{c}{sinC}$，将$a=2，c=\sqrt{2}$代入得到$sinC=\cfrac{1}{2}$，故$C=\cfrac{\pi}{6}$。

静雅凤中$\;\cdot\;$三角函数和解三角形专题$\;\cdot\;$针对性训练题 (2017高考真题 文科全国卷1的第15题) 已知$\alpha\in(0，\cfrac{\pi}{2})$，$tan\alpha=2$，则$cos(\alpha-\cfrac{\pi}{4})$=__________。

---

分析：由$tan\alpha=2，\alpha\in(0，\cfrac{\pi}{2})$，故有$sin\alpha=2k，cos\alpha=k(k>0)$， 由平方关系可知$k=\cfrac{\sqrt{5}}{5}$，故$sin\alpha=\cfrac{2\sqrt{5}}{5}$，$cos\alpha=\cfrac{\sqrt{5}}{5}$， 则$cos(\alpha-\cfrac{\pi}{4})=cos\alpha\cdot cos\cfrac{\pi}{4}+sin\alpha\cdot sin\cfrac{\pi}{4}=\cfrac{\sqrt{5}}{5}\times \cfrac{\sqrt{2}}{2}+\cfrac{2\sqrt{5}}{5}\times \cfrac{\sqrt{2}}{2}=\cfrac{3\sqrt{10}}{10}$。

转载于:https://www.cnblogs.com/wanghai0666/p/6213875.html