前几天看到一个问题“已知一个四面体的六条棱长（假定棱长必定可以构成一个四面体），如何计算这个四面体的体积”，但是当我进行了推导后写作后，目前找不到该问题了——如有人找到请告知，谢谢！
实际上这个问题是“三斜求积术”的扩展：就是从“已知三角形的三边长
（有读者可能会问，这不是“海伦公式”的扩展么？——我的回答是：是的！但是我这里说“三斜求积术”是有我的理由的，请耐心看下去）
先来说“三斜求积术”吧：秦九韶在《数书九章》提出了“三斜求积术”，翻译成现代语言就是：如果已知三角形的三边长
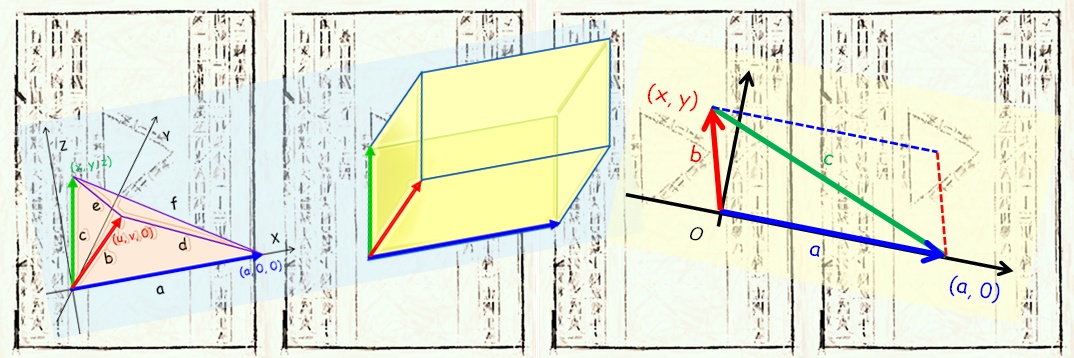
现在来推导一下这个公式：将这个三角形放入平面直角坐标系之中，三个顶点分别是
（由此可以得到
在本人之前文章：
行列式就是体积/面积？——（一）
行列式就是体积/面积？——（二）
行列式就是体积/面积？——（三）
中已说明，
- 两个不共线的向量“形成的平行四边形”的“带符号”面积就是它们的行列式值。
- 三个不共面的向量“形成的平行六面体”的“带符号”体积就是它们的行列式值。
于是三角形面积的平方是向量
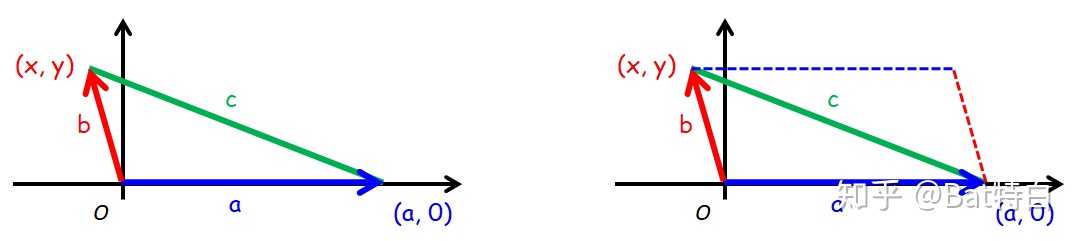
而“形成的平行四边形”的“带符号”面积也就是
（处理方案1）由前可知
于是三角形面积的平方值等于平行四边形面积的平方值的1/4，继而那么该三角形的（无向）面积为
利用
若令
（处理方案2）其实，面积的平方这个行列式
（处理方案3）前同方案2，之后考虑极端情况，即退化的三角形
好了，下面来类似地处理“已知四面体的六个棱长
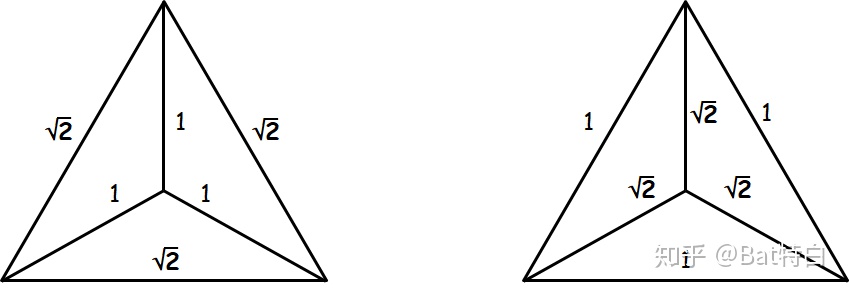
首先我们需要约束“六条棱”的长度的关系：假设长为
这样约束的原因在于：下左的四面体和下右的四面体体积并不相等。
将这个四面体放入三维坐标系之中，四个顶点分别是
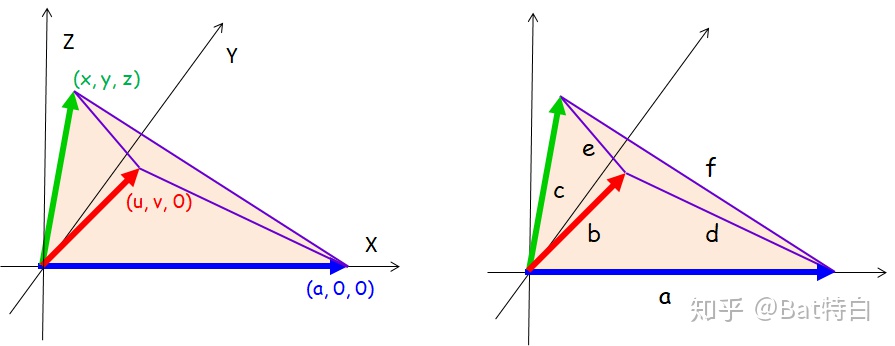
于是这个四面体的（无向）体积就是三个向量
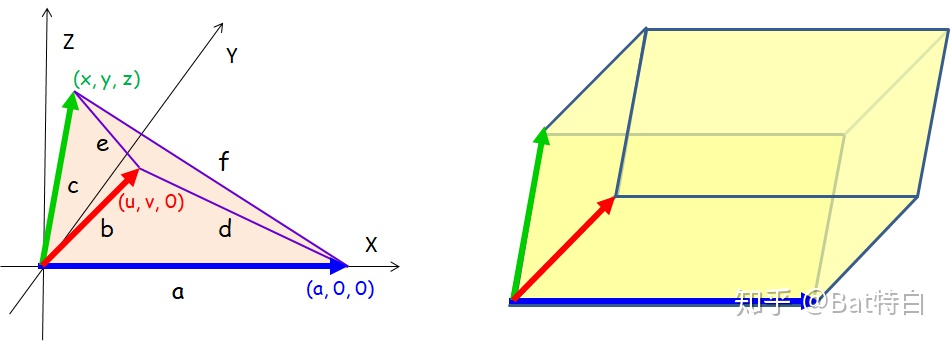
而平行六面体的体积等于
这个行列式不能再如前地简单分解了——其实我觉得这个行列式已经足够简单了。
那么，已知四面体的六个棱长
最后讨论几句吧：
- 对于
这个行列式，它一定是变量
的多项式且次数不超过6。如果要类似之前（处理方案3）的分析的话，那么我感觉需要讨论平面三角形中6个线段长度之间的关系（这时四面体退化为二维的三角形）；而且此时变量
的地位不再是完全相同的了，问题将变得复杂。
- 对于更高维的情况，求单纯形的体积，那么首先就是“边长”的“顺序”关系，之前2维情况时，
的次序没关系，但是到了3维情况，边长的“次序”不同，可能得到的四面体就不同，体积也不同。
- 最后是（简单初等而不严谨滴说）为什么由三个向量围成的四面体的（无向）体积是同样这三个向量围成的平行六面体的（无向）体积的1/6。其方法和论证三角形面积是相对应的平行四边形的面积的一半的方法是类似的，平面情况是“1分为2”，三维情况是“1分为6”（不引入积分了，用到了一个未加证明的结果——底面积高相同的三棱锥体积相同）：
- 先斜着一刀把平行六面体切成两个全等的三棱柱。
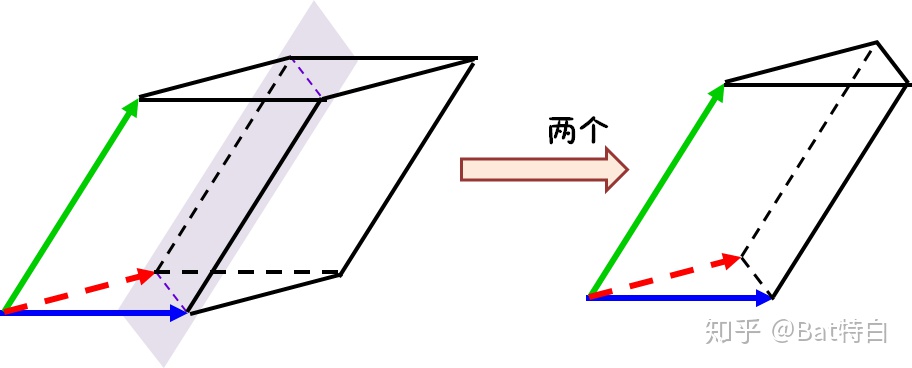
- 然后再把一个三棱柱切成一个我们需要的和四面体一个四棱锥。
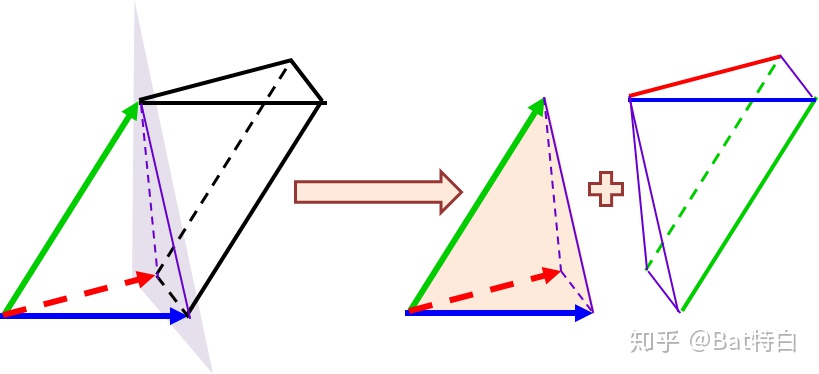
- 再把四棱锥二分，则粉色的和黄色的体积相等。
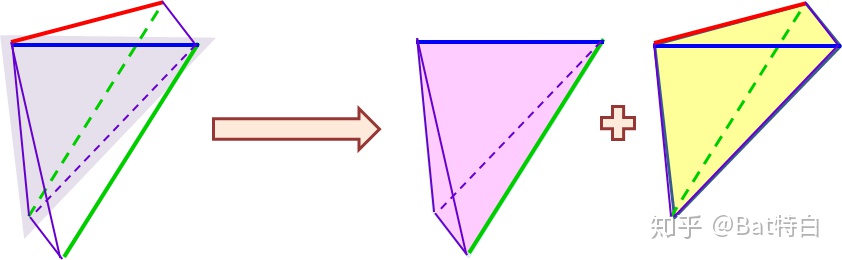
- 于是平行六面体分解为六个三棱锥，其中粉色的和黄色的明显体积相等：
- 下面看粉色的和肉色的（我们需要的四面体）三棱锥，也是一个四棱锥的二分，所以体积也相等。
- 所以我们需要四面体的（无向）体积是相应的平行六面体的（无向）体积的1/6。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
