576. Out of Boundary Paths

最新推荐文章于 2020-11-25 15:34:28 发布

weixin_34015860

最新推荐文章于 2020-11-25 15:34:28 发布

阅读量93

点赞数

文章标签：数据结构与算法

原文链接：http://www.cnblogs.com/jxr041100/p/8115093.html

版权

There is an m by n grid with a ball. Given the start coordinate (i,j) of the ball, you can move the ball to adjacent cell or cross the grid boundary in four directions (up, down, left, right). However, you can at most move N times. Find out the number of paths to move the ball out of grid boundary. The answer may be very large, return it after mod 109 + 7.

Example 1:

Input:m = 2, n = 2, N = 2, i = 0, j = 0
Output: 6
Explanation:

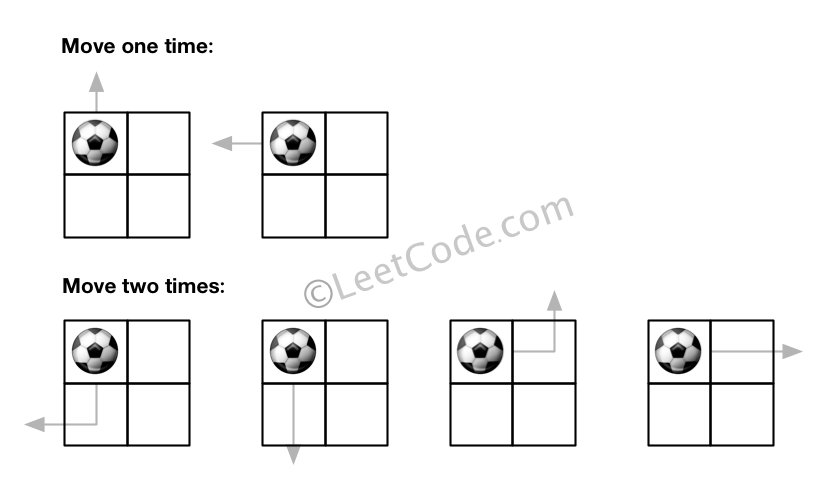
Example 2:

Input:m = 1, n = 3, N = 3, i = 0, j = 1
Output: 12
Explanation:

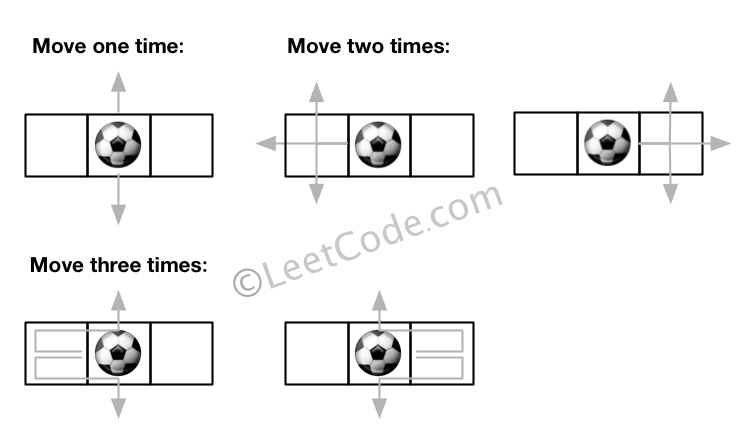
class Solution {
public:
    int findPaths(int m, int n, int N, int i, int j) {
        vector<vector<vector<int>>> dp(N + 1, vector<vector<int>>(m, vector<int>(n, -1)));       
        return dfs(m,n,N,i,j,dp);       
    }
private:   
    int dfs(int m,int n,int N,int i,int j,vector<vector<vector<int>>> &dp)
    {
        if(N==0) return 0;
        int res = 0;
        if(dp[N][i][j]!=-1) return dp[N][i][j];
        vector<pair<int,int>> dirs = {{-1,0},{1,0},{0,-1},{0,1}};
        for(auto dir:dirs)
        {
            int next_i = i+dir.first;
            int next_j = j+dir.second;
            if(next_i<0 || next_j <0 || next_i>=m || next_j >=n) //out of boundary
                res = res+1;
            else 
                res+=dfs(m,n,N-1,next_i,next_j,dp);
            res = res%1000000007;
        }
        res = res%1000000007; 
        dp[N][i][j] =  res;
        return res;
    }
};

动态规划的解法

class Solution {
public:
    int findPaths(int m, int n, int N, int i, int j) {
        vector<vector<vector<int>>> dp(N + 1, vector<vector<int>>(m, vector<int>(n, 0)));
        for (int k = 1; k <= N; ++k) {
            for (int x = 0; x < m; ++x) {
                for (int y = 0; y < n; ++y) {
                    long long v1 = (x == 0) ? 1 : dp[k - 1][x - 1][y];
                    long long v2 = (x == m - 1) ? 1 : dp[k - 1][x + 1][y];
                    long long v3 = (y == 0) ? 1 : dp[k - 1][x][y - 1];
                    long long v4 = (y == n - 1) ? 1 : dp[k - 1][x][y + 1];
                    dp[k][x][y] = (v1 + v2 + v3 + v4) % 1000000007;
                }
            }
        } 
        return dp[N][i][j];
    }
};