三维齿轮 matlab,基于MATLAB和SolidWorks的弧齿锥齿轮三维精确建模

(3)绘制大端、小端齿廓渐开线。MATLAB软件不仅擅长处理数组的各种运算，而且其图形显示功能强大，适合于弧齿锥齿轮的渐开线的建立。因此将如下数据输入到MATLAB中，绘制渐开线：

将MATLAB生成的渐开线导人SolidWorks中，步骤如下：① 用assignin函数将要保存的变量返回到MATLAB的workplace中，双击workplace中的变量，将数据全部复制后粘贴到记事本中；② 打开SolidWorks中的曲线按钮，通过X，Y，Z的曲线选项，点击后出现曲线表格，选文件类型为Text File，找到渐开线文件(xianl，xian2)；③ 点打开，又回到曲线文件表格，点确定，渐开线曲线即进入SolidWorks。值得注意的是虽然Z值为零，但SolidWorks仍认为此曲线是空间曲线，因此在平面上使用时，可用转换实体工具将其转化为平面曲线。将渐开线移动到合适的位置后，将其沿着Z轴旋转角度A1。

建立通过大端渐开线和大端基圆的点4，再穿过大端中心线和点4来建立基准面4，然后将基准面4旋转角度A2来建立基准面5，作为镜像平面来镜像大、小端渐开线。

(4)创建齿坯实体、扫描轨迹和齿廓线。在前视基准面内绘制齿坯曲线，旋转成齿坯实体；根据刀具半径、螺旋角和齿轮的旋转方向绘制刀盘圆线和夹角35°切线来绘制扫描轨迹，如图3所示。

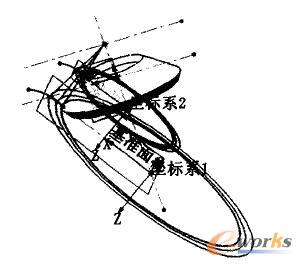
图3 扫描轨迹和齿廓图

(5)单击SolidWorks“特征”工具栏中的“扫描”绘制出一个齿，再通过“旋转”工具得到弧齿锥齿轮的完整模型，如图4所示。

图4 齿轮完整模型

2 结论

本文采用MATLAB来绘制弧齿锥齿轮的大端和小端齿面的齿廓线，将MATLAB和SolidWorks相结合使得建立的弧齿锥齿轮模型更加精确，为后续的有限元分析奠定了基础。

责任编辑：郝秋红