BZOJ 2434 阿狸的打字机（fail树）

题目链接：http://61.187.179.132/JudgeOnline/problem.php?id=2434

题意：阿狸喜欢收藏各种稀奇古怪的东西，最近他淘到一台老式的打字机。打字机上只有28个按键，分别印有26个小写英文字母和'B'、'P'两个字母。经阿狸研究发现，这个打字机是这样工作的：

（1）输入小写字母，打字机的一个凹槽中会加入这个字母(这个字母加在凹槽的最后)。

（2）按一下印有'B'的按键，打字机凹槽中最后一个字母会消失。

（3）按一下印有'P'的按键，打字机会在纸上打印出凹槽中现有的所有字母并换行，但凹槽中的字母不会消失。
例如，阿狸输入aPaPBbP，纸上被打印的字符如下：
a
aa
ab
我们把纸上打印出来的字符串从1开始顺序编号，一直到n。打字机有一个非常有趣的功能，在打字机中暗藏一个带数字的小键盘，在小键盘上输入两个数(x,y)（其中1≤x,y≤n），打字机会显示第x个打印的字符串在第y个打印的字符串中出现了多少次。阿狸发现了这个功能以后很兴奋，他想写个程序完成同样的功能，你能帮助他么？

 

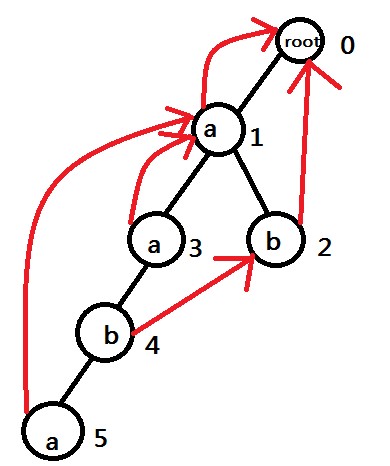
思路：首先，将所有串插入trie建立自动机。那么对于一个询问（x,y），最简单的做法是枚举root到y路径上的每个字母，然后这个字母沿着他的fail指针一直走，若能走到x，那么这个位置就能匹配到x，答案加1。这种做法过于暴力。我们想下，对于每个x，我们用V[i]记录下能够通过fail指针转移到x的所有位置，然后使用V数组DFS一次，得到一个DFS序列，并记录每个点在DFS序列的两个位置，那么我们就能得到，能够转移到x的所有字母都在x的两个位置的中间。比如aPbPBaPbPaP得到的自动机为：

旁边的数字为串的编号。相应的V数组为：V[0]={2,1},V[1]={5,3},V[2]={4}，那么我们得到的DFS序列为:0 2 4 4 2 1 5 5 3 3 1 0。那么对于每个询问（x，y），当DFS到y的时候，我们只要知道此时有多少个字母在两个x之间即可。比如询问(2,4)，我们从root一直DFS到4，中间插入了1,3,4，到了4时我们查询两个2之间的和就是答案，很明显只有4一个，答案就是1。当我们查询(1,5)是，我们DFS到5时插入了1,3,4,5,到了5时，查询两个1之间的，很明显有三个是1,3,5,答案就是3。另外，在DFS返回时要将插入的删除。这里，使用树状数组维护比较简单。

struct node
{
    int next[26],p,fail;


    void init()
    {
        clr(next,0);
        fail=-1;
    }
};


node a[N];
int e;
int strMap[N],strCnt;


void insert(string s)
{
    a[0].init(); e++;
    int i,k,p=0;
    FOR0(i,SZ(s))
    {
        if(s[i]>='a'&&s[i]<='z')
        {
            k=s[i]-'a';
            if(a[p].next[k]==0)
            {
                a[e].init();
                a[p].next[k]=e++;
            }
            a[a[p].next[k]].p=p;
            p=a[p].next[k];
        }
        else if(s[i]=='P') strMap[++strCnt]=p;
        else if(s[i]=='B') p=a[p].p;
    }
}

vector<int> V[N];


void build()
{
    queue<int> Q;
    Q.push(0);
    int i,u,k,t;
    while(!Q.empty())
    {
        u=Q.front();
        Q.pop();


        FOR0(i,26) if(a[u].next[i])
        {
            t=a[u].next[i];
            k=a[u].fail;
            while(k!=-1&&!a[k].next[i]) k=a[k].fail;
            if(k==-1) a[t].fail=0;
            else a[t].fail=a[k].next[i];


            Q.push(t);
            V[a[t].fail].pb(t);
        }
    }


}

string s;
int n,m;
vector<pair<int,int> > q[N];
int ans[N],L[N],R[N],S[N];


void add(int x,int det)
{
    while(x<N)
    {
        S[x]+=det;
        x+=x&-x;
    }
}


int get(int x)
{
    int ans=0;
    while(x)
    {
        ans+=S[x];
        x-=x&-x;
    }
    return ans;
}


void DFS(int u)
{
    L[u]=++m;
    int i;
    FOR0(i,SZ(V[u])) DFS(V[u][i]);
    R[u]=++m;
}


void dfs(int u)
{
    int i,x,y,p;
    FOR0(i,SZ(q[u]))
    {
        x=q[u][i].first;
        y=q[u][i].second;
        ans[y]=get(R[x])-get(L[x]-1);
    }
    FOR0(i,26) if(a[u].next[i])
    {
        p=a[u].next[i];
        add(L[p],1);
        dfs(p);
        add(L[p],-1);
    }
}


int main()
{
    RD(s); insert(s); build(); RD(n);
    int i,x,y;
    FOR1(i,n)
    {
        RD(x,y);
        q[strMap[y]].pb(MP(strMap[x],i));
    }
    DFS(0); dfs(0);
    FOR1(i,n) PR(ans[i]);
}

转载于:https://www.cnblogs.com/jianglangcaijin/p/3470901.html