代码随想录day15--图论

主要过程就是一圈一圈

容器需要能保存所遍历过的元素：队列 ， 栈 ，数组

队列：操作受限制的线性表，先进先出，一般应用的问题：速度不匹配，多用户竞争资源。

顺序存储：头指针 front 指向对头元素，尾指针 rear 指向队尾元素的下一个位置。

队列顺序存储的顺序存储类型的描述：

登录后复制

#define MaxSize 50  //定义队列中元素的最大个数
typedef struct{
   ElemType data[MaxSize];  //存放队列元素   
   int front,rear;  //队头指针和队尾指针   
   } SqQueue;

• 1.
• 2.
• 3.
• 4.
• 5.

操作：

登录后复制

初始状态（队空条件）：Q.front == Q.rear == 0
进队操作：队不满时，                          先送值到队尾元素，再将队尾指针加1
出队操作：队不空时，                                                        先取队头元素值，再将队头指针加1

• 1.
• 2.
• 3.

链式存储： 链队列，一个同时带有队头指针和对尾指针的单链表，头指针指向对头结点，尾指针指向队尾结点，即单链表最后一个结点

代码描述：

登录后复制

typedef struct{  //链式队列结点
   ElemType data;
   struct LinkNode *next;
}LinkNode;
typedef struct{  //链式队列
   LinkNode *front,*rear;  //队列的队头和队尾指针
}LinkQueue;

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.

如果bfs是使用队列，需要保证统一的顺时针或者逆时针。（先进先出）

如果bfs是使用栈，那么就需要第一圈是顺时针遍历，第二圈是逆时针遍历，第三圈是顺时针遍历。（先进后出）

栈：只允许在一端进行插入和删除操作的线性表，栈顶（top)线性表允许插入删除的一端，栈底（bottom), 空栈

应用：进制转换，表达式求值，括号匹配

顺序结构：一组地址连续的存储单元存放自栈底到栈顶的数据元素，同时附设一个指针（top)指示当前栈顶元素的位置。

代码结构表示：

登录后复制

#define MaxSize 50  //定义栈中元素的最大个数
typedef struct{
   ElemType data[MaxSize];  //存放栈中元素
   int top;  //栈顶指针
   }SqStack;

• 1.
• 2.
• 3.
• 4.
• 5.

操作：

登录后复制

栈顶指针：S.top，初始时设置：S.top = -1，栈顶元素：S.data[S.top]
进栈操作：栈不满时，栈顶指针先加1，再送值到栈顶元素。
出栈操作：栈非空时，先去栈顶元素值，再将栈顶指针减1。
栈空条件：S.top == -1，栈满条件：S.top == MaxSize-1，栈长：S.top + 1
注意：顺序栈的入栈操作受数组上界的约束，当对栈的最大使用空间估计不足时，有可能会出现栈上溢出。
栈和队列的判空、判断条件，根据实际给的条件不同而变化

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.

栈的链式存储：链栈，优点：便于多个栈共享存储空间，通常单链表，没有头结点,LHead指向栈顶元素，

代码表示栈的链式存储的结构类型

登录后复制

typedef struct Linknode{
   ElemType data;  //数据域
   struct Linknode *next;  //指针域
}*LiStack;  //栈定义类型

• 1.
• 2.
• 3.
• 4.

 【数据结构】栈和队列知识大全

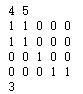
题目：给定一个由 1（陆地）和 0（水）组成的矩阵，你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成，并且四周都是水域。你可以假设矩阵外均被水包围。

输入描述： 第一行包含两个整数 N, M，表示矩阵的行数和列数。 后续 N 行，每行包含 M 个数字，数字为 1 或者 0。

输出描述： 输出一个整数，表示岛屿的数量。如果不存在岛屿，则输出 0。

登录后复制

4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出：3

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.

注意题目中每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成 （dfs的应用）

本题思路，是用遇到一个没有遍历过的节点陆地，计数器就加一，然后把该节点陆地所能遍历到的陆地都标记上。

在遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。

1：确认递归函数和参数  x,y ,visited 访问标记矩阵  ,grid-----作为二维列表来表示地图，邻接矩阵

2：终止条件就是全部遍历完成

3：处理目前搜索结点出发的路径

登录后复制

direction = [[0, 1], [1, 0], [0, -1], [-1, 0]]  # 四个移动方向：上、右、下、左


def dfs(grid, visited, x, y):
    """
    对一块陆地进行深度优先遍历并标记
    """
    print(f"Visiting ({x}, {y})")  # 打印当前访问的坐标
    for i, j in direction:
        next_x = x + i
        next_y = y + j
        # 下标越界，跳过       len(grid)=行数  len(grid[0])=列数
        if next_x < 0 or next_x >= len(grid) or next_y < 0 or next_y >= len(grid[0]):
            continue  #结束当前循环直接进入下一循环
        # 未访问并且有的的陆地，标记并调用深度优先搜索
        if not visited[next_x][next_y] and grid[next_x][next_y] == 1:
            visited[next_x][next_y] = True
            print(f"Moving to ({next_x}, {next_y})")  # 打印移动到的新坐标
            dfs(grid, visited, next_x, next_y)


if __name__ == '__main__':  
    # 版本一
    n, m = map(int, input().split())
    
    # 邻接矩阵
    grid = []
    for i in range(n):
        grid.append(list(map(int, input().split())))
    
    # 访问表
    visited = [[False] * m for _ in range(n)]
    
    res = 0
    for i in range(n):
        for j in range(m):
            # 判断：如果当前节点是陆地，res+1并标记访问该节点，使用深度搜索标记相邻陆地。
            if grid[i][j] == 1 and not visited[i][j]:
                res += 1
                visited[i][j] = True
                dfs(grid, visited, i, j)
    
    print(res)

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.
• 15.
• 16.
• 17.
• 18.
• 19.
• 20.
• 21.
• 22.
• 23.
• 24.
• 25.
• 26.
• 27.
• 28.
• 29.
• 30.
• 31.
• 32.
• 33.
• 34.
• 35.
• 36.
• 37.
• 38.
• 39.
• 40.
• 41.
• 42.
• 43.

登录后复制

direction = [[0, 1], [1, 0], [0, -1], [-1, 0]]  # 四个方向：上、右、下、左
def dfs(grid, visited, x, y):
    """
    对一块陆地进行深度优先遍历并标记
    """
    # 与版本一的差别，在调用前增加判断终止条件
    if visited[x][y] or grid[x][y] == 0:
        return
    visited[x][y] = True

    for i, j in direction:
        next_x = x + i
        next_y = y + j
        # 下标越界，跳过
        if next_x < 0 or next_x >= len(grid) or next_y < 0 or next_y >= len(grid[0]):
            continue
        # 由于判断条件放在了方法首部，此处直接调用dfs方法
        dfs(grid, visited, next_x, next_y)
if __name__ == '__main__':
    # 版本二
    n, m = map(int, input().split())

    # 邻接矩阵
    grid = []
    for i in range(n):
        grid.append(list(map(int, input().split())))

    # 访问表
    visited = [[False] * m for _ in range(n)]

    res = 0
    for i in range(n):
        for j in range(m):
            # 判断：如果当前节点是陆地，res+1并标记访问该节点，使用深度搜索标记相邻陆地。
            if grid[i][j] == 1 and not visited[i][j]:
                res += 1
                dfs(grid, visited, i, j)
    print(res)

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.
• 15.
• 16.
• 17.
• 18.
• 19.
• 20.
• 21.
• 22.
• 23.
• 24.
• 25.
• 26.
• 27.
• 28.
• 29.
• 30.
• 31.
• 32.
• 33.
• 34.
• 35.
• 36.
• 37.
• 38.

原创作者: u_16373090 转载于: https://blog.51cto.com/u_16373090/11909062