A Parallel Challenge ballgame is played on a rectangular filed. The filed is surrounded by a wall; balls will bounce off the walls if they run into it. The rule of bouncing is the same as light (In figure 1,angle 1 equals angle 2). Near the edges of the fields are a number of goals where points can be scored. Goals are rectangular areas lying near the edges of the field but within the field boundaries. When the game starts there are a number of balls placed at random locations on the field. A player can move to a ball, pick it up, and throw (of course, it is not football, why not use hand?) it. At the start of each game there are also a number of “nets” distributed at various locations on the edges of the field. A player can move to and pick up one of these nets, and can then use them to “trap” players on other teams by throwing the net on top of them. Once a player is trapped beneath a net, that player cannot do anything more in the game until a teammate comes and lifts the net from the trapped player. A player may “tackle” another player, normally in an attempt to dislodge a ball being carried by the other player (although it is also legal to tackle a player who is not carrying a ball).

The objective of each team is to write their MyPlayer class so that their players (the five instances of the class) operate in a coordinated fashion, taking advantage of the various ways to score points while at the same time avoiding both hazards on the game filed and impediments thrown at them by players from other teams. The winner of a game is the team whose players score the largest total number of points.
There are many ways to score points:
(1) Successful Tackle (tackle not caught by Referees)
(2) Opponent’s Failed Tackle
(3) Throwing a net on one or more opponents
(4) Lifting a net off a teammate
And of course, the normal approach: (5) Carry or throw the balls into goals. This is also the easiest way to score points. In order to get more chance to make a ball into the goal, it is better to throw a ball to a goal once you get it. The ball may be blocked by other player, but the probability is low, because a thrown ball moves at the maximum speed allowed in the game, and the player can not catch up with it. So the only way it is blocked is that some player is just on the direction, which the ball moves. And because the ball will bounce off the wall when it hits the wall, it is not necessary to throw a ball straight to a goal (see figure 2). But the more times the ball bounces off the wall, the higher probability that other player will head off it. So we only consider the ball bounces off the wall no more than once.
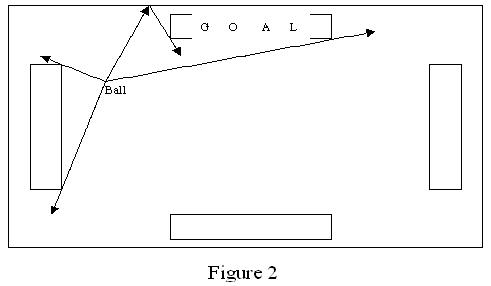
Here is our problem. Given the range of the field, the position of the ball and the goals, the size of the goals, your task is to calculate how many percents of the direction that the team can score points through method (5).
1
100 100 -100 -100
0 0
1
10 10 -10 2028.34%
在杭电ACM上看到了这个十分有趣的题目,与大家分享之。
问题描述:
ACM/ICPC全球总决赛前有个比赛叫做“The Parallel Challenge Ballgame”。这个比赛在一个快速并行编程考验技巧、策略无危险的游戏中给了所有队伍一个同其他参赛队伍比拼编程技能的平台。规则是这样的:每个参赛小组编写一个叫做MyPlayer的定义了游戏玩家功能的C++类,在游戏中将用该类产生5个实例,组成一个5个人比赛小组。这个比赛将在全球最快的电脑——“蓝色基因”超级计算机上运行。
Parallel Challenge ballgame游戏在一个长方形场地内进行。这个区域四周被墙壁环绕,球碰到墙壁就会反弹。球体反弹的规则就和光线反射是一样的(在图1中角1等于角2)。靠近区域边界的地方有一些可以的得分的目标。当游戏开始时候,一些球将会被随机的放置在区域内。玩家需要移动到球体所在的位置,把它捡起来并抛出去(这并不是足球嘛,为什么不可以用手抛呢?)。每次游戏开始前,区域的边缘将会初始化一些网,网可以网住玩家,一个玩家一旦被网住,那么他就不能再继续做其他任何事情了,直到队友将他救出。玩家可以攻击其他的玩家,最常见的就是撞开携带球的玩家(尽管对付无球的玩家是合乎规则的)。

得分的方法有很多:
(1)成功攻击了对手(对裁判无效)
(2)对手攻击失败了
(3)用网网住对手
(4)从网里救回队友
当然最常规的得分方法是:(5)将球带入或扔进球门。为了获得更多破门机会,最好是一拿到球就往球门里扔。因为扔出的球有着游戏允许的最快速度,玩家不可能赶得上它的,当然球也有可能被对方截住,不过这个机率太小了,只有当对方玩家恰好在球移动方向上时才可能发生。同时由于球可以击中墙壁反弹,所以不直接往球门里面扔球也可能得分(参见图2)。但是球反弹的次数越多,其他球员截住球的机率也将增加。所以我们只考虑球反弹不超过一次的情况。

输入:
输入的第一行是一个表示测试用例个数的整数,第二行包含四个数字1, y1, x2, y2,(x2, y2) (-1000 <= x1, y1, x2, y2 <= 1000)。这四个数字代表了场地范围的坐标区域。接下来是球门的个数n,接下来的n行代表的是第i个球门的范围的对角坐标。你可以假设球门和球都在区域范围内,球进入了球门或碰到了边界都算得分。
输出:
结果是一个百分数,需要四舍五入精确到小数点后两位。样本输出格式如下:
1
100 100 -100 -100
0 0
1
10 10 -10 20
28.34%题目分析:
本题可以转化为在一定坐标范围内求已知点通过反弹一次或直接到指定区域的角度范围,如图所示,角B为直接能够到达指定区域的角度,角A是小球经过左面墙壁反弹后能够穿过指定区域的角度,同理右边、下方墙壁小球均有可能反弹一次经过指定区域。
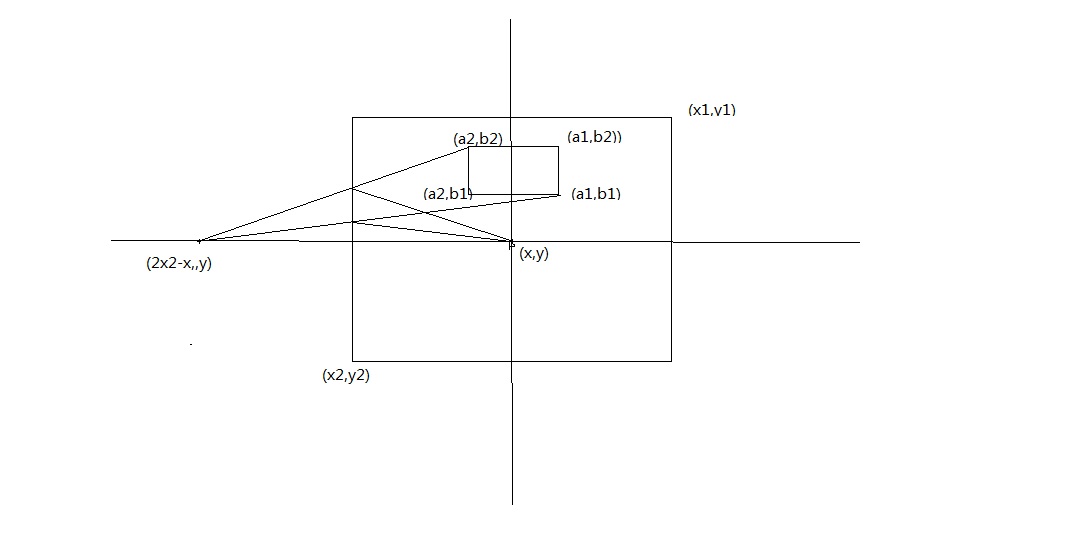
设小球坐标(x,y),设矩形区域(x1,y1),(x2,y2),设球门四个顶点分别为A(a1,b1),B(a1,b2),C(a2,b1),D(a2,b2)
现推导角A的计算公式:
小球B关于(x2,0)可以看作图中的(-100,0)对称点为A‘(2x2-x,y),
向量A’C(2x2-x-xi2,y-yi1),向量A‘D(2x2-x-xi2,y-yi2)
cos(angleA)=向量A‘C*向量A'D/(|A'C|*|A'D|);
angleA = acos(向量A‘C*向量A'D/(|A'C|*|A'D|));
同理可推导其余公式.
java代码实现如下:
import java.text.NumberFormat;
import java.util.Scanner;
public class Ballgame {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
NumberFormat nf = NumberFormat.getInstance();
nf.setMaximumFractionDigits(2);
int total = 0,count = 0;
total = Integer.parseInt(scanner.next());
while(count++ < total){
double x1,y1,x2,y2;//矩形区域(x1,y1),(x2,y2)
x1 = Double.parseDouble(scanner.next());
y1 = Double.parseDouble(scanner.next());
x2 = Double.parseDouble(scanner.next());
y2 = Double.parseDouble(scanner.next());
double x,y;//小球坐标(x,y)
x = Double.parseDouble(scanner.next());
y = Double.parseDouble(scanner.next());
int ttotal = 0,tcnt = 0;
ttotal = Integer.parseInt(scanner.next());
double totalDegree = 0;
while(tcnt++ < ttotal){
double a1,b1,a2,b2;//球门区域(a1,b1),(a2,b2)
a1 = Double.parseDouble(scanner.next());
b1 = Double.parseDouble(scanner.next());
a2 = Double.parseDouble(scanner.next());
b2 = Double.parseDouble(scanner.next());
//求角度
//(x,y)左边对称点(2*x2-x,y)与(a1,b1),(a2,b2)所形成的夹角
totalDegree += calculateDegree(2*x2-x,y, a1, b1, a2, b2);
//(x,y)右边对称点(2*x1-x,y)与(a1,b2),(a2,b1)所形成的夹角
totalDegree += calculateDegree(2*x1-x,y, a1, b2, a2, b1);
//(x,y)下方对称点(x,2*y2-y)与(a1,b1),(a2,b1)所形成的夹角
totalDegree += calculateDegree(x,2*y2-y, a1, b1, a2, b1);
//(x,y)与(a1,b1),(a2,b1)所形成的夹角
totalDegree += calculateDegree(x,y, a1, b1, a2, b1);
}
//计算可能的值
System.out.println(nf.format(totalDegree*100/(2*Math.PI)) + "%");
}
}
/**
* 计算 (a,b)与点(x1,y1)和(a,b)与(x2,y2)所形成的夹角
* @param a
* @param b
* @param x1
* @param y1
* @param x2
* @param y2
* @return 夹角的度数
*/
public static double calculateDegree(double a,double b,double x1,double y1, double x2,double y2){
//向量1
double tmpX1 = x1 -a;
double tmpY1 = y1 -b;
double length1 = Math.sqrt(tmpX1*tmpX1 + tmpY1*tmpY1);
//向量2
double tmpX2 = x2 -a;
double tmpY2 = y2 -b;
double length2 = Math.sqrt(tmpX2*tmpX2 + tmpY2*tmpY2);
//cos(a) = 向量1*向量2/(|向量1|*|向量2|)
double degree = Math.acos(1.0*(tmpX1*tmpX2 + tmpY1*tmpY2)/(length1*length2));
return degree;
}
}c++语言实现如下:
#include <iostream>
#include <math.h>
using namespace std;
double calculateDegree(double a,double b,double x1,double y1,double x2,double y2);
int main(){
int total = 0;
int cnt = 0;
cin >> total;
while(cnt++ < total){
double x1,y1,x2,y2;//矩形区域(x1,y1),(x2,y2)
cin >> x1 >> y1 >> x2 >> y2;
double x,y;//小球坐标(x,y)
cin >> x >> y;
int ttotal = 0,tcnt = 0;
cin >> ttotal;
double totalDegree = 0;
while(tcnt++ < ttotal){
double a1,b1,a2,b2;//球门区域(a1,b1),(a2,b2)
cin >> a1 >> b1 >> a2 >> b2;
//求角度
//(x,y)左边对称点(2*x2-x,y)与(a1,b1),(a2,b2)所形成的夹角
totalDegree += calculateDegree(2*x2-x,y, a1, b1, a2, b2);
//(x,y)右边对称点(2*x1-x,y)与(a1,b2),(a2,b1)所形成的夹角
totalDegree += calculateDegree(2*x1-x,y, a1, b2, a2, b1);
//(x,y)下方对称点(x,2*y2-y)与(a1,b1),(a2,b1)所形成的夹角
totalDegree += calculateDegree(x,2*y2-y, a1, b1, a2, b1);
//(x,y)与(a1,b1),(a2,b1)所形成的夹角
totalDegree += calculateDegree(x,y, a1, b1, a2, b1);
}
cout.precision(4); //用两位小数显示
double result = totalDegree*100/(2*3.1415926);
cout << result << '%' << endl;
}
return 0;
}
double calculateDegree(double a,double b,double x1,double y1,double x2,double y2){
//向量1
double tmpX1 = x1 -a;
double tmpY1 = y1 -b;
double length1 = sqrt(tmpX1*tmpX1 + tmpY1*tmpY1);
//向量2
double tmpX2 = x2 -a;
double tmpY2 = y2 -b;
double length2 = sqrt(tmpX2*tmpX2 + tmpY2*tmpY2);
//cos(a) = 向量1*向量2/(|向量1|*|向量2|)
double degree = acos(1.0*(tmpX1*tmpX2 + tmpY1*tmpY2)/(length1*length2));
return degree;
}
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








