
本文继续写猫爪定理——即密克定理的应用。

1
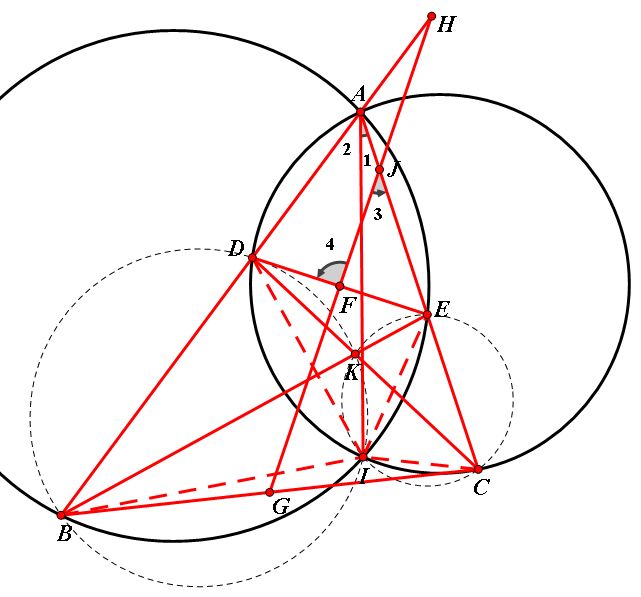
已知:如图,D,E在AB,AC上,F,G为DE,BC中点,
FG交BA于H,△ABE,△ADC外接圆交于AI。
求证:∠IAC=∠FHA
思路分析一:
此题显然是上篇最后一题的推广形式,
因此考虑类似的方法。
若∠IAC=∠FHA,则∠IAB=∠HJA,
只需证明sin∠IAC:sin∠IAB=sin∠FHA:sin∠HJA,
分别利用相似及正弦定理计算得到他们都等于EC:DB即得。


证明一:
设∠IAC=∠1,∠IAB=∠2,
∠AJH=∠3,∠DHF=∠4。
由正弦定理得:DH:sin4=DF:sinH,
即DHsinH=DFsin4,结合DF=FE,
同理即得:
DHsinH=DFsin4=EFsin4=EJsin3,
故sinH:sin3=EJ:DH,
同理可得sinH:sin3=CJ:BH,
由等比定理得:
sinH:sin3=(EJ-CJ):(DH-BH)=EC:DB,
又显然I为AB,AC,BE,CD构成的完全四边形密克点,
从而△IDB∼△ICE,
故sinH:sin3=EC:DB=CI:ID=sin1:sin2,
又∠H+∠3=∠1+∠2,
故∠1=∠H。
即∠IAC=∠FHA。

思路分析二:
类似思路一,
但是感觉sinH:sin3=EC:DB的证明除了用正弦定理计算以外,
应该还有更几何的方法,
看到中点想到中位线定理是合情合理的,
作出BE(或CD)中点,由中位线定理即得。
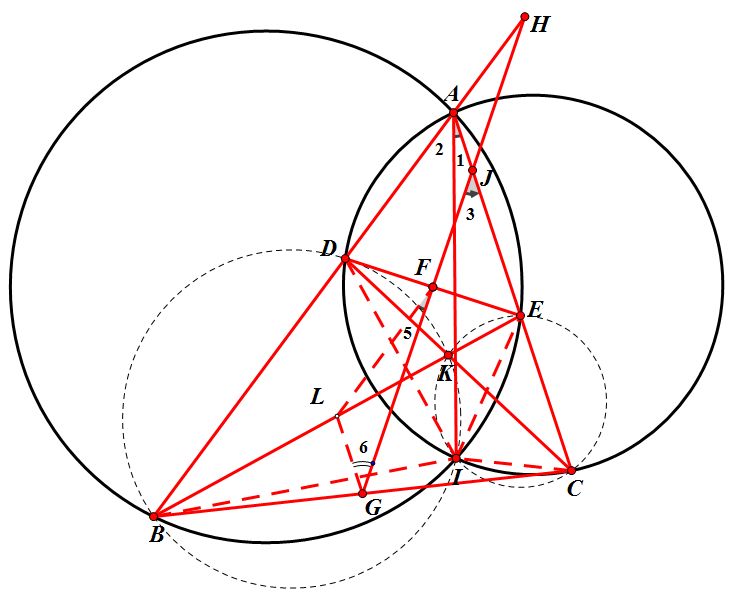


证明二:同思路一,取BE中点L,连接FL,FG,
设∠IAC=∠1,∠IAB=∠2,
∠AJH=∠3,∠LFG=∠5,
∠LGF=∠6。
由中位线定理得LF//AB,LG//CE
故∠5=∠H,∠3=∠6,
且BD=2LF,CE=2GL,
由正弦定理得
sinH:sin3=sin5:sin6=GL:LF=EC:DB,
同1得sin1:sin2=CI:ID=EC:DB=sinH:sin3,
又∠H+∠3=∠1+∠2,
故∠1=∠H。
即∠IAC=∠FHA。

注:
1)本结论是上篇[1]最后一题的推广,当DE//BC时,H与A重合,此题即为那题。当然此题证明思路也和那题类似。我们在上篇及原来的文章中虽然对此题都做了深入的探讨,但是思考永远是没有止境的,如此题所示,她还能进一步推广到更一般的完全四边形中。这样一来,我们就能把此结论作为一般的完全四边形的一个优美而重要的性质:完全四边形牛顿线与一边的夹角,等于密克点和此边上顶点连线与此直线过上述顶点的临边的夹角。
2)上述两种证法也是常见的,在本公众号早期的文章阿基米德折弦定理系列文章中[2]中第3题中即用到了同样的方法,当本题中EC=DB时,本题即为那题。当然,阿基米德折弦定理其实和密克定理之间也是息息相关的,其本质上也是密克定理。因为可以看到这里面的顺相似三角形对,事实上北极点即为密克点。感兴趣的读者可以对照理解。

2
过等腰△ABC底边BC上一点P引PM//CA交AB于M;引PN//BA交AC于N.
作点P关于MN的对称点P’.
求证:P’点在△ABC外接圆上.
(1949年匈牙利第50届数学竞赛,
2002年全国初中数学联赛)
思路分析1:
依题意可得M为△BPP'的外心,
N为△CPP'的外心,
从而即得∠BP'C=∠A,从而得证。
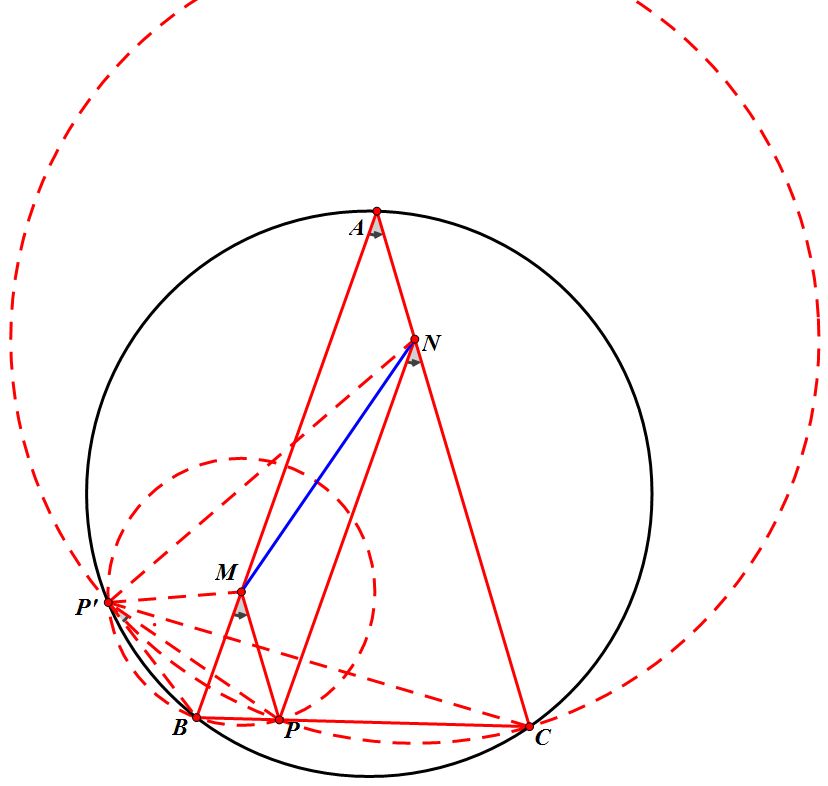


证明1:
依题意易得MB=MP=MP',
从而M为△BPP'的外心,
类似的,N为△CPP'的外心,
故2∠BP'P=∠BMP=∠A=∠PNC=2∠PP'C,
即∠BP'C=∠A,
故BP'AC共圆。
即P’点在△ABC外接圆上.

思路分析2:
显然AMPN为平行四边形,
由对称得P'MNA共圆,
BP'AC共圆
<=>∠P'BA=∠P'CA,
<=>∠AMP'=∠ANP',
<=>P'MNA。
从而得证。



证明2:
依题意AMPN为平行四边形,
由对称得
∠BAC=∠MPN=∠MP'N,
故P'MNA共圆。
则∠AMP'=∠ANP',
又MB=MP=MP',
及NC=NP=NP',
故∠P'BA=∠P'CA,
故BP'AC共圆,
即P’点在△ABC外接圆上。

注:
1)本题最早出现于1949年,是一个非常经典的问题,很早就流行于各类辅导资料中,印象中我上中学的时候就经常见到此题,感觉具有浓郁的外国风味,应该是很早的国外的考试题,这次经过多方面查找资料后方找到其出处。
2)本题是非常漂亮、人见人爱的一个结论,所以初中数学联赛又拿出来考也在意料之中。自从国家取消了统一的初中数学联赛以后,她的影响力每况愈下,试题质量也严重下滑,题目往往陈陈相因。几何题目基本都是一些经典的题目的再现。
3)上述两种证明方法貌离神合,本质上都是利用对称性及线段相等得到结果,不过一个是用外心,一个是用四点共圆。当然本题还有其他的证明思路,例如证明∠BAC=∠BP’C,那样就要稍微麻烦一点了,不过最终还是殊途同归,本质上与上述证明也没有区别。
4)从动态角度看,本题等价于证明当P在BC上运动时,P’的轨迹为△ABC外接圆。
5)本题似乎和密克点无关,不过看到共点的顺相似△P’BM∽△P’CN,应该就能想到可能会和密克点有关。事实上,P’即为AB,AC,BC,MN构成的完全四边形的密克点。
6)本图中还隐藏着大量结论,还能进行大幅的推广和加强,几乎每个几何高手都对此结构有深入的思考和研究。近年来很多大型考试中都有很多题目是在此结构基础上加强得到的。后面的几篇文章会详细介绍。

参考文献
[1] 猫爪定理及其应用之二
[2] 阿基米德折弦定理之一

点我留言
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








