前言
前面一篇文章,笔者就二叉查找树进行了一些解释与实现,这篇文章笔者将会就平衡二叉树
做一些总结与实现。读者若不了解二叉查找树的话,可以参考这篇文章:
http://blog.csdn.net/kiritor/article/details/8889176
在学习平衡二叉树之前,我们先回顾下二叉查找树的特点和性质。
基于二叉查找树以下的操作是低性能的:
1、如果我们向一棵空的二叉查找树中插入一个预先排好序的序列的(升序),根据插入
操作我们会发现形成的二叉树结点层次太深,且没有左儿子结点。情况如下:
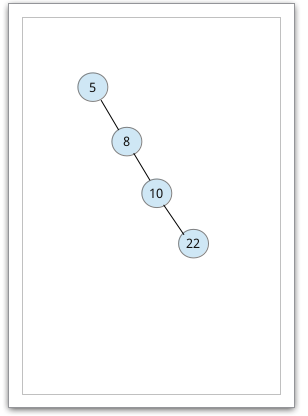
这样就造成了二叉树的深度过深,明显不合理。
2、在二叉查找树的情况下,对于任意个单一的操作我们不再保证O(logN)的时间界
但是我们可以证明的是在连续M次操作时间花费可能达到O(MlogN),消耗太高了。
基于上述的原因,我们就需要考虑平衡二叉树了。
平衡二叉树
首先需要明白的是平衡二叉树是对二叉查找的一种改进,对于二叉查找树的一个明显的
缺点就是,树的结构仍旧具有极大的变动性,最坏的情况下就是一棵单支二叉树,丢失了二叉
查找树一些原有的优点。
平衡二叉树定义(AVL):它或者是一棵空树,或者是具有一下性质的二叉查找树--
它的结点左子树和右子树的深度之差不超过1,而且该结点的左子树和右子树都是一棵
平衡二叉树。
平衡因子:结点左子树的深度-结点右子树的深度。(0、1、-1)。
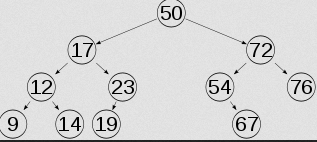
转换为平衡二叉树之后的二叉树为:
平衡保持
很显然,平衡二叉树旨在“平衡”二字,其平衡是如何保持的呢?换句话说,二叉查找树是
如何转换为平衡二叉树的呢?就像上面两张图片,到底如何转换的呢?基本的思想就是:
当二叉查找树中插入一个结点时,首先检查是否因为插入而破坏了平衡。若破坏了则
找出其中的最小不平衡二叉树,在保持二叉查找树特性的情况下,调整最小不平衡子树中结
点之间的关系,以达到平衡。
最小不平衡二叉树指距离插入结点最近且以平衡因子的绝对值大于1的结点作为根的子树。
那么最小不平衡二叉树结点的关系到底是如何进行调整的呢?分为四种情况讨论。
四种不平衡类型
有四种情况可以导致二叉树不平衡:(以根结点为例)
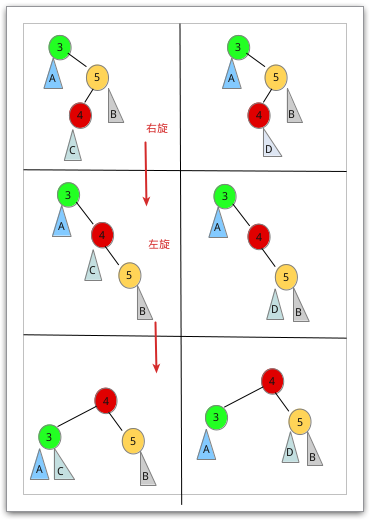
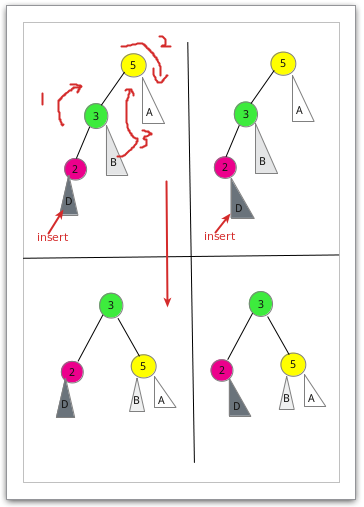
1、LL型(右旋操作):插入一个新的结点到根结点的左子树的左子树,导致根结点的平衡
因子1变为2。
其右旋操作我们以一个具体的例子掌握:
以第一列为例,在结点2的左子树插入结点D,插入后2结点的平衡因子变为1,导致
结点5(根结点)的平衡因子变为2,则结点5为根结点的子树是最小不平衡子树。调整时
将结点5的左孩子3向右上旋转代替结点5为根结点,将根结点右下旋转为3的右子树的根
结点,而结点3的原右子树变为结点5的左子树。
在结点2的右孩子处插入的情况原理一样的。
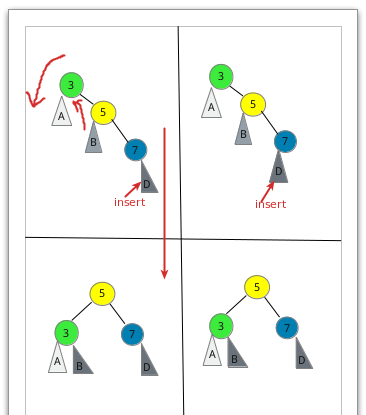
2、RR型(左旋操作):插入一个新的结点到根结点的右子树的右子树,导致根结点的平衡
因子1变为2。
其具体的操作我们同样以一个例子为例:
其操作步骤与右旋操作没有什么太大的区别,这里笔者就不详述过程了。
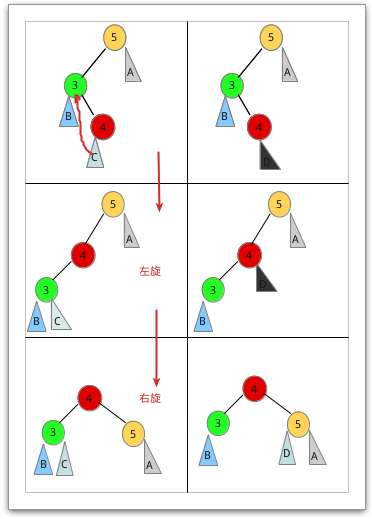
3、LR型(左旋+右旋):在根结点的左孩子的右子树上插入结点,插入情况笔者就
不给实例图了。直接演示其操作过程。
可见的是LR型需要两次的旋转才能达到要求,不过在进行右旋操作的时候需要注意C
的位置。
4、RL型(右旋+左旋)在根结点的右子树的左子树上插入结点。同样以一个实例图
来演示操作。
完整源码实现:
根据上述的旋转操作,我们简单的实现二叉平衡树:
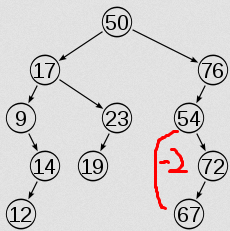
package com.kiritor; /** *二叉平衡树简单实现 *@author kiritor */ public class AvlTree< T extends Comparable< ? super T>> { private static class AvlNode< T>{//avl树节点 AvlNode( T theElement ) { this( theElement, null, null ); } AvlNode( T theElement, AvlNode< T> lt, AvlNode< T> rt ) { element = theElement; left = lt; right = rt; height = 0; } T element; // 节点中的数据 AvlNode< T> left; // 左儿子 AvlNode< T> right; // 右儿子 int height; // 节点的高度 } private AvlNode< T> root;//avl树根 public AvlTree( ) { root = null; } //在avl树中插入数据,重复数据复略 public void insert( T x ) { root = insert( x, root ); } //在avl中删除数据,这里并未实现 public void remove( T x ) { System.out.println( "Sorry, remove unimplemented" ); } //在avl树中找最小的数据 public T findMin( ) { if( isEmpty( ) ) System.out.println("树空");; return findMin( root ).element; } //在avl树中找最大的数据 public T findMax( ) { if( isEmpty( ) ) System.out.println("树空"); return findMax( root ).element; } //搜索 public boolean contains( T x ) { return contains( x, root ); } public void makeEmpty( ) { root = null; } public boolean isEmpty( ) { return root == null; } //排序输出avl树 public void printTree( ) { if( isEmpty( ) ) System.out.println( "Empty tree" ); else printTree( root ); } private AvlNode< T> insert( T x, AvlNode< T> t ) { if( t == null ) return new AvlNode< T>( x, null, null ); int compareResult = x.compareTo( t.element ); if( compareResult < 0 ) { t.left = insert( x, t.left );//将x插入左子树中 if( height( t.left ) - height( t.right ) == 2 )//打破平衡 if( x.compareTo( t.left.element ) < 0 )//LL型(左左型) t = rotateWithLeftChild( t ); else //LR型(左右型) t = doubleWithLeftChild( t ); } else if( compareResult > 0 ) { t.right = insert( x, t.right );//将x插入右子树中 if( height( t.right ) - height( t.left ) == 2 )//打破平衡 if( x.compareTo( t.right.element ) > 0 )//RR型(右右型) t = rotateWithRightChild( t ); else //RL型 t = doubleWithRightChild( t ); } else ; // 重复数据,什么也不做 t.height = Math.max( height( t.left ), height( t.right ) ) + 1;//更新高度 return t; } //找最小 private AvlNode< T> findMin( AvlNode< T> t ) { if( t == null ) return t; while( t.left != null ) t = t.left; return t; } //找最大 private AvlNode< T> findMax( AvlNode< T> t ) { if( t == null ) return t; while( t.right != null ) t = t.right; return t; } //搜索(查找) private boolean contains( T x, AvlNode t ) { while( t != null ) { int compareResult = x.compareTo( (T) t.element ); if( compareResult < 0 ) t = t.left; else if( compareResult > 0 ) t = t.right; else return true; // Match } return false; // No match } //中序遍历avl树 private void printTree( AvlNode< T> t ) { if( t != null ) { printTree( t.left ); System.out.println( t.element ); printTree( t.right ); } } //求高度 private int height( AvlNode< T> t ) { return t == null ? -1 : t.height; } //带左子树旋转,适用于LL型 private AvlNode< T> rotateWithLeftChild( AvlNode< T> k2 ) { AvlNode< T> k1 = k2.left; k2.left = k1.right; k1.right = k2; k2.height = Math.max( height( k2.left ), height( k2.right ) ) + 1; k1.height = Math.max( height( k1.left ), k2.height ) + 1; return k1; } //带右子树旋转,适用于RR型 private AvlNode< T> rotateWithRightChild( AvlNode< T> k1 ) { AvlNode< T> k2 = k1.right; k1.right = k2.left; k2.left = k1; k1.height = Math.max( height( k1.left ), height( k1.right ) ) + 1; k2.height = Math.max( height( k2.right ), k1.height ) + 1; return k2; } //双旋转,适用于LR型 private AvlNode< T> doubleWithLeftChild( AvlNode< T> k3 ) { k3.left = rotateWithRightChild( k3.left ); return rotateWithLeftChild( k3 ); } //双旋转,适用于RL型 private AvlNode< T> doubleWithRightChild( AvlNode< T> k1 ) { k1.right = rotateWithLeftChild( k1.right ); return rotateWithRightChild( k1 ); } // Test program public static void main( String [ ] args ) { AvlTree< Integer> t = new AvlTree< Integer>( ); final int NUMS = 200; final int GAP = 17; System.out.println( "Checking... (no more output means success)" ); for( int i = GAP; i != 0; i = ( i + GAP ) % NUMS ) t.insert( i ); t.printTree( ); System.out.println(t.height(t.root)); } }知道的是二叉树的层树应该为199,但是实际情况如何呢?
转载于:https://blog.51cto.com/kiritor/1226767






















 921
921











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








