《数学建模：基于R》一一

本节书摘来自华章计算机《数学建模：基于R》一书中的第1章，第1.1节,作者：薛　毅 更多章节内容可以访问云栖社区“华章计算机”公众号查看。

1.1　数据的描述性分析

在建立随机模型之前,首先要分析数据的主要特征,也就是数据的数字特征.这些特征通常是均值、方差,或者是数据服从什么分布.只有在确定了这些特征之后,才能建立起符合实际的模型.
本节介绍数据的描述性分析的统计方法,以及完成此类分析的R函数.
1.1.1　数据的数字特征
已知一组试验（或观测）数据为X1,X2,…,Xn,它们可以是从所要研究的对象的全体——总体X中取出的,这n个观测值就构成一个样本.数据分析的任务就是要对这n个数据进行分析,提取数据中包含的有用信息.
1.样本均值
样本均值是数据的平均数,也就是样本的算术平均值,其计算公式为X=1n∑ni=1Xi（1.1）它描述数据取值的平均位置.
在R中,mean()函数用于计算样本均值,其使用格式为mean(x, trim = 0, na.rm = FALSE, ...)参数x为需要计算均值的对象(如向量、矩阵、数组或数据框).
trim为(0,0.5)之间的数(默认值为0),表示在计算均值之前,去掉两端数据的百分比,即计算截尾均值.
na.rm为逻辑变量,表示能否处理带有缺失数据(NA)的样本,默认值为FALSE.
...为附加参数.
例如,> x <- c(0:10, 50); xm <- mean(x)

c(xm, mean(x, trim = 0.10))
［1］ 8.75 5.50程序中的c()为连接函数,将数据连接成向量.

2.样本方差
方差是描述数据取值分散性的一个度量.样本方差是样本相对于均值的偏差平方和的平均,记为S2,即S2=1n-1∑ni=1(Xi-X)2（1.2）其中X为样本均值.样本方差的开方称为样本标准差,记为S,即S=1n-1∑ni=1(Xi-X)2（1.3）在R中,可用var()函数计算样本方差,其使用格式为var(x, y = NULL, na.rm = FALSE, use)参数x为数值向量、矩阵或数据框.当y为NULL(默认值)时,计算样本x的方差;当y为数值向量、矩阵或数据框时,计算样本x与y的协方差.
na.rm为逻辑变量,表示能否处理带有缺失数据(NA)的样本,默认值为FALSE.
计算样本标准差的函数是sd(),其使用格式为sd(x, na.rm = FALSE)参数的意义与var()函数相同.
例如,> x<-c(12, 9, 11, 5, 1, 4, 8, 3, 2, 10, 6, 7)

var(x)

［1］ 13

sd(x)

［1］ 3.6055513.中位数
中位数就是数据排序位于中间位置的值.如果数据按顺序排列,对于奇数个数据,中位数就是中间位置的数据;对于偶数个数据,中位数就是中间两个数据的平均值.
在R中,可用median()函数计算样本的中位数,其使用格式为median(x, na.rm = FALSE)参数x为需要计算中位数的数值型向量.
na.rm为逻辑变量,表示能否处理带有缺失数据(NA)的样本,默认值为FALSE.
例如,> x <- c(12, 9, 11, 5, 1, 4, 8, 3, 2, 10, 6, 7, NA)

median(x)

［1］ NA

median(x, na.rm = TRUE)

［1］ 6.54.分位数
分位数可以看成中位数的推广,如中位数就是0.5分位数.常用的还有14分位数和34分位数,分别称为下四分位数和上四分位数.p分位数又可称为第100p百分位数,如中位数可称为第50百分位数,下四分位数可称为第25百分位数,上四分位数可称为第75百分位数.
在R中,quantile()函数计算样本的分位数,其使用格式为quantile(x, probs = seq(0, 1, 0.25), na.rm = FALSE,
names = TRUE, type = 7, ...)参数x为样本构成的数值向量.
probs为数值向量,数值在0与1之间,表示需要计算的分位数,默认值为0,0.25,0.50,0.75和1.
na.rm为逻辑变量,表示能否处理带有缺失数据(NA)的样本,默认值为FALSE.
names为逻辑变量,表示是否将百分位数作为返回值中变量的属性,默认值为TRUE.
type为1～9之间任何一个整数,表示计算分位数的算法,默认值为7.
例如,> quantile(1:10)
　　0%　25%　50%　75%　100%
　1.003.255.507.7510.005.极差与四分位极差
样本极差(记为R)是一组数据的最大值与最小值之差,其计算公式为R=max(X)-min(X)（1.4）其中X是由样本构成的向量.样本极差是描述样本分散性的数字特征.数据越分散,其极差越大.由于极差是利用一组数据两端的信息,因此容易受到极端值的影响.
在R中,与极差有关的函数有max(), min()和range(),其使用格式为max(..., na.rm = FALSE)
min(..., na.rm = FALSE)
range(..., na.rm = FALSE)参数...为数据构成的向量.
max()函数的返回值是最大值,min()函数的返回值是最小值,range()函数的返回值是由最小值和最大值构成的二维向量.
因此,计算极差的程序为R <- max(x) - min(x)
r <- range(x); R <- r［2］ - r［1］其中x是由样本构成的向量.
样本的上、下四分位数之差称为四分位极差（或半极差）,记为R1,即R1=Q3-Q1（1.5）它也是度量样本分散性的重要数字特征,特别对于具有异常值的数据,它作为分散性度量具有稳健性.因此,它在稳健性数据分析中具有重要作用.
由半极差的定义(式（1.5））,可得到半极差的计算公式R1 <- quantile(x, 3/4) - quantile(x, 1/4)其中x是由样本构成的向量.
例1.1　某班有31名学生,某门课的考试成绩如下：
25　45　50　54　55　61　64　68　72　75　75
78　79　81　83　84　84　84　85　86　86　86
87　89　89　89　90　91　91　92　100
求这门课程考试成绩的平均值、中位数、方差、极差和四分位极差.
解　编写一个统一计算平均值、中位数、方差、极差和四分位极差等统计量的函数(程序名:discript.R).discript <- function(x){
　　R1 <- quantile(x, 3/4, names = FALSE)
　　　　　　- quantile(x, 1/4, names = FALSE)
　　data.frame(
　　　　n = length(x), max = max(x), min = min(x),
　　　　R = max(x) - min(x), R1 = R1,
　　　　mean = mean(x), median = median(x),
　　　　sd = sd(x)
　　)
}程序中的length()函数是计算向量的长度,即维数.
将数据写入数据文件(exam0101.data),然后调用该函数计算：X <- scan("exam0101.data")
source("discript.R"); discript(X)在程序中,scan()函数是从数据文件中读取数据,source()是将编写好的函数调入内存,其计算结果如下：nmaxminRR1meanmediansd
13110025751876.7096884 16.69769计算结果说明:共有31名学生的成绩,最高分为100分,最低分为25分,极差是75分,半极差是18分,平均分数为76.7分,中位数分数为84分,标准差为16.7分.
1.1.2　随机变量的分布
1.随机变量
从一个总体中抽取不同的样本,分析各个样本所获得的点估计往往不尽相同,这种表现出变异性特征的量称为变量.
在进行统计试验以前,一般并不知道某一试验的确切结果,但是可以赋予试验结果以实际数量的一个函数.因此这一变量称为随机变量.随机变量常用大写字母表示,如X,Y,Z.它们可能出现的具体结果或数值则可用小写字母表示,如x,y,z.
最常见的随机变量有两类.一类是以计数形式表示的随机变量,称为离散型随机变量;另一类是取值在某个有限或无限区间的随机变量,称为连续型随机变量.
2.分布函数
描述一个随机变量X,不仅要说明它能够取哪些值,而且还要关心它取这些值的概率.对任意的实数x,令F(x)=P{X≤x},　x∈(-∞,+∞)（1.6）则称F(x)为随机变量X的分布函数,也称为累积分布函数.
从直观上看,分布函数F(x)是一个定义在(-∞,+∞)上的实值函数,F(x)在点x处取值为随机变量X落在区间(-∞，x］上的概率.
3.概率函数与概率密度函数
如果随机变量X的全部可能取值只有有限多个或可列无穷多个,则称X为离散型随机变量.
对于离散型随机变量X，可能取值为xk的概率为P{X=xk}=pk,　k=1,2,…（1.7）则称式(1.7)为离散型随机变量X的分布律.
离散型随机变量的分布函数为F(x)=P{X≤x}=∑xk≤xP{X=xk}=∑xk≤xpk（1.8）对于随机变量X,如果存在一个定义在(-∞，+∞)上的非负函数f(x),使得对于任意实数x,总有F(x)=P{X≤x}=∫x-∞f(t)dt,　-∞4.分位数
设X为随机变量,对任给的0<α<1,若存在xα,使得P{X≤xα}≥1-α,　P{X>xα}≥α（1.10）则称xα为X的上α分位数(或上α分位点).对任给的0

xp}≥1-p（1.11）则称点xp为X的下p分位数(或下p分位点).由式(1.10)和式(1.11)可以得到上、下分位数之间的关系:上α分位数就是下1-α分位数.
由分位数的关系式(1.10)(或式(1.11))可知,分位数不是唯一的.但对于连续型随机变量,分位数确实是唯一的,此时,可将式(1.11)改写成F(xp)=p其中F(x)为随机变量X的分布函数.对于连续型随机变量,分布函数是严格单调递增的,所以可将下p分位数表示为逆分布函数,即xp=F-1(p)(1.12)由上、下分位数之间的关系式,上α分位数可表示为xα=F-1(1-α)（1.13）1.1.3　常用的分布
1.正态分布
若随机变量X的概率密度函数为f(x)=12πσexp-(x-μ)22σ2,　-∞0)为两个常数,则称X服从参数为μ和σ2的正态分布,也称为Gauss（高斯）分布,记作X～N(μ,σ2).若X～N(μ,σ2),则F(x)=∫x-∞12πσe-(t-μ)22σ2dt,　-∞pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)参数x或q为纯量或向量,表示概率密度函数或分布函数的自变量.
p为纯量或向量,描述分位点的概率.
mean为纯量或向量,描述均值参数(即μ)的取值,默认值为0.
sd为纯量或向量,描述标准差参数(即σ)的取值,默认值为1.
log， log.p为逻辑变量,表示概率值p是否由其对数值log(p)给出,默认值为FALSE.
lower.tail为逻辑变量,表示是否作下尾运算.取TRUE(默认值)表示F(x)=P{X≤x},对应的分位数是下分位数.取FALSE表示F(x)=P{X>x},对应的分位数是上分位数.
图1.1描绘的是不同参数的正态分布的概率密度函数图,分别是：μ=0,σ=0.5;μ=2,σ=0.5；μ=0,σ=1.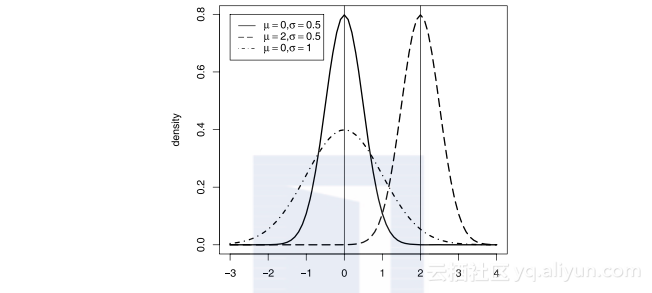

图1.1　正态分布的概率密度函数
例1.2　设X～N(μ,σ2),分别计算P{X-μ≤σ},P{X-μ≤2σ}和P{X-μ≤3σ},以及正态分布的上0.025分位点Z0.025.
解　当X～N(μ,σ2)时,Z=X-μσ～N(0,1),所以用标准正态分布计算即可.> x <- 1:3; p <- pnorm(x) - pnorm(-x); p
［1］ 0.6826895 0.9544997 0.9973002这就是通常所说的3σ原则,即在1σ,2σ和3σ区间内的概率分别为68.3%,95.4%和99.7%.
注意:qnorm()函数提供的是下分位点,计算上α分位点等价于计算下1-α分位点,所以计算程序为> alpha <- 0.025; z <- qnorm(1-alpha); z
［1］ 1.9599642.χ2分布
如果Zi～N(0,1)(i=1,2,…,n),且Zi是相互独立的,则称X=Z21+Z22+…+Z2n（1.16）为自由度为n的χ2分布,记为X~χ2(n).如果Zi～N(δ,1),则称X为非中心化的χ2分布,记X~χ2(n,δ),称δ为非中心化参数.
在R软件中,用chisq表示χ2分布,其调用格式如下：dchisq(x, df, ncp=0, log = FALSE)
pchisq(q, df, ncp=0, lower.tail = TRUE, log.p = FALSE)
qchisq(p, df, ncp=0, lower.tail = TRUE, log.p = FALSE)参数df为自由度,ncp为非中心化参数(即δ),其余参数的意义与正态分布函数相同.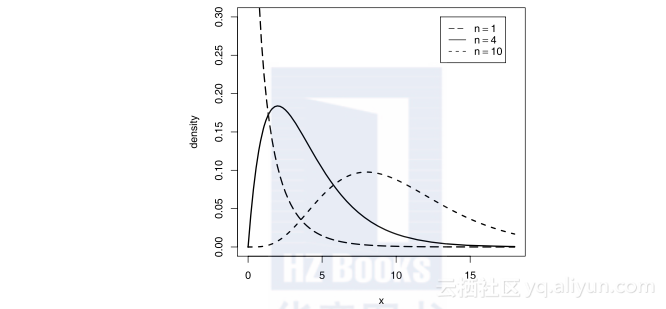

图1.2描绘的是χ2分布的概率密度函数在不同参数下的图形.
图1.2　χ2分布的概率密度函数
3.t分布
如果随机变量Z~N(0,1),X~χ2(n)且X与Z相互独立,则称T=ZX/n（1.17）为自由度为n的t分布,记为T~t(n).如果Z～N(δ,1),则称T为非中心化t分布,记为T~t(n,δ),称δ为非中心化参数.
在R中,t分布的使用格式是dt(x, df, ncp = 0, log = FALSE)
pt(q, df, ncp = 0, lower.tail = TRUE, log.p = FALSE)
qt(p, df, ncp = 0, lower.tail = TRUE, log.p = FALSE)参数df为自由度,ncp为非中心化参数(即δ),其余参数的意义与正态分布函数相同.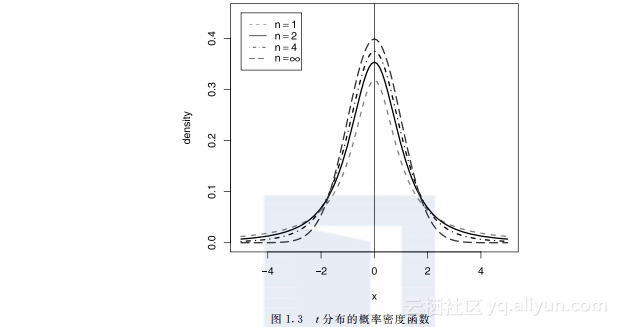

图1.3描绘的是t分布的概率密度函数在不同参数下的图形.
图1.3　t分布的概率密度函数
4.F分布
如果随机变量X~χ2(n1),Y~χ2(n2)且相互独立,则称F=X/n1Y/n2（1.18）为第1自由度为n1和第2自由度为n2的F分布,记为F~F(n1,n2).如果X~χ2(n1,δ),则称F为非中心化F分布,记为F~F(n1,n2;δ),称δ为非中心化参数.
在R中,F分布的使用格式为df(x, df1, df2, ncp = 0, log = FALSE)
pf(q, df1, df2, ncp = 0, lower.tail = TRUE, log.p = FALSE)
qf(p, df1, df2, ncp = 0, lower.tail = TRUE, log.p = FALSE)参数df1为第1自由度,df2为第2自由度,ncp为非中心化参数(即δ),其余参数的意义与正态分布函数相同.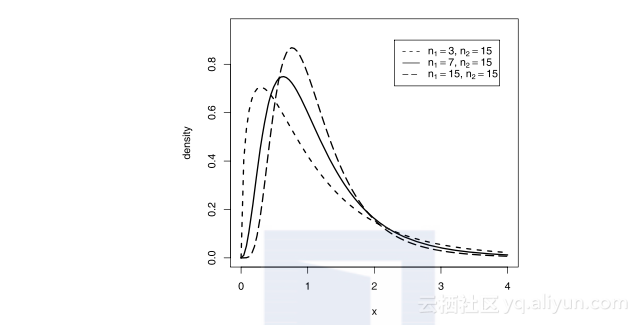

图1.4描绘的是F分布的概率密度函数在不同参数下的图形.
图1.4　F分布的概率密度函数
1.1.4　数据的图形描述
可以通过数据的图形描述判断数据的分布情况,比如是否来自于正态分布等.
1.直方图
直方图又称柱状图或质量分布图,是一种统计报告图,由一系列高度不等的纵条纹或线段表示数据的分布情况.直方图是用来展示连续数据分布的常用工具,用来估计数据的概率分布.
在R中,hist()函数绘制数据的直方图,其使用格式为hist(x, breaks = "Sturges",
　　freq = NULL, probability = !freq,
　　include.lowest = TRUE, right = TRUE,
　　density = NULL, angle = 45, col = NULL, border = NULL,
　　main = paste("Histogram of" , xname),
　　xlim = range(breaks), ylim = NULL,
　　xlab = xname, ylab,
　　axes = TRUE, plot = TRUE, labels = FALSE,
　　nclass = NULL, warn.unused = TRUE, ...)参数x为向量,表示直方图的数据.
breaks为数值、向量或字符串,描述直方图的断点.
freq为逻辑变量,表示在绘制直方图时是否使用频数,取TRUE(默认值)表示使用频数, 取FALSE表示使用概率密度.
border为数字或字符串,描述直方外框的颜色.
labels为逻辑变量,表示是否标出频数或密度,默认值为FALSE.
例1.3　画出例1.1中学生考试成绩的直方图.
解　这里给出两种画法,主要目的是展示hist()函数的功能.X <- scan("exam0101.data")

figure 1

hist(X, col = "lightblue", border = "red",
　　labels = TRUE, ylim = c(0, 14.5))

figure 2

r <- hist(X, freq = FALSE, density = 10,
　　　　　angle = 15+30*1:6)
text(r$mids, 0, r$counts, adj=c(.5, -.5), cex = 1.2 )
lines(density(X), col = "blue", lwd = 2)
x <- seq(from = 20, to = 100, by = 1)
lines(x, dnorm(x, mean(X), sd(X)), col = "red", lwd = 2)第一张图绘出的是频数直方图,增加了直方图和外框的颜色,以及相应的频数.第二张图使用线条作阴影,并利用text()函数标出频数,用lines()绘出数据的密度曲线和正态分布密度曲线.所绘图形如图1.5所示.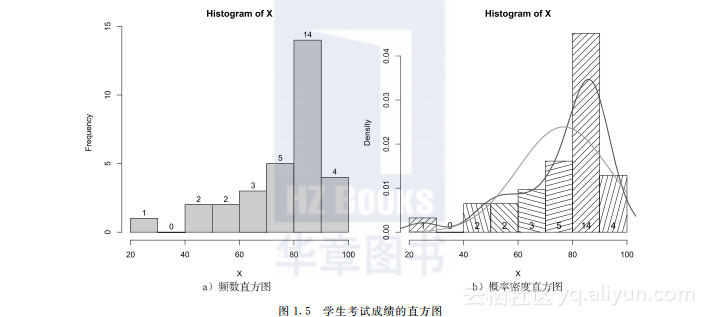

图1.5　学生考试成绩的直方图
从图形(特别是图1.5b)可以看出,本次学生的考试成绩不服从正态分布.
2.Q-Q图
Q-Q图是一种散点图,对应于正态分布的Q-Q图,就是由标准正态分布的分位数为横坐标,样本值为纵坐标的散点图.利用正态Q-Q图可以鉴别样本数据是否近似于正态分布.
在R中,qqnorm()函数的功能是绘出数据的正态Q-Q图,qqline()函数是在Q-Q图上增加一条理论直线,qqplot()函数画出数据集的Q-Q图,它们的使用格式为qqnorm(y, ylim, main = "Normal Q-Q Plot",
　　　　xlab = "Theoretical Quantiles",
　　　　ylab = "Sample Quantiles",
　　　　plot.it = TRUE, datax = FALSE, ...)
qqline(y, datax = FALSE, distribution = qnorm,
　　　　probs = c(0.25, 0.75), qtype = 7,...)
qqplot(x, y, plot.it = TRUE, xlab = deparse(substitute(x)),
　　　　ylab = deparse(substitute(y)),...)参数x为向量,表示第1组样本的数据(仅用于qqplot()函数).y为向量,表示第2组样本的数据,或仅表示样本数据.
main为字符串,表示图题.xlab和ylab为字符串,分别表示x轴和y轴的标签.
plot.it为逻辑变量,表示是否绘图,默认值为TRUE.
例1.4　画出例1.1中学生考试成绩的正态Q-Q图.
解　写出R程序(程序名:exam0104.R)如下：X <- scan("exam0101.data"); qqnorm(X); qqline(X)所绘图形如图1.6所示.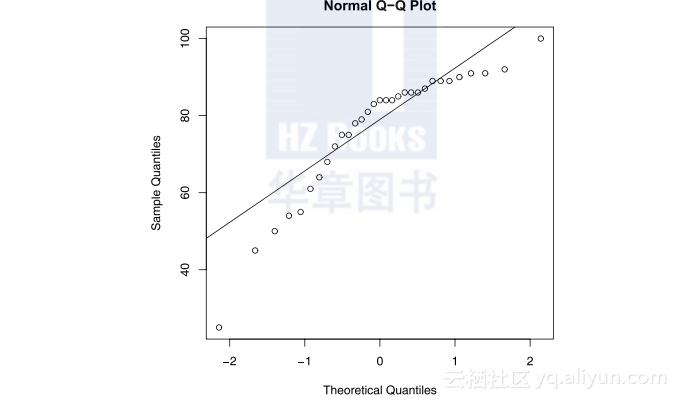

图1.6　学生考试成绩的正态Q-Q图
从图1.6可以看出,散点与直线偏差太多,因此,学生考试成绩不服从正态分布,这一点与直方图的结论是一致的.