简单二叉树

简单二叉树的建树，遍历

一、L2-006. 树的遍历

给定一棵二叉树的后序遍历和中序遍历，请你输出其层序遍历的序列。这里假设键值都是互不相等的正整数。

输入格式：

输入第一行给出一个正整数N（<=30），是二叉树中结点的个数。第二行给出其后序遍历序列。第三行给出其中序遍历序列。数字间以空格分隔。

输出格式：

在一行中输出该树的层序遍历的序列。数字间以1个空格分隔，行首尾不得有多余空格。

输入样例：

7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

输出样例：

4 1 6 3 5 7 2

#include <iostream>
#include <queue>
#include <vector>
#include <cstdio>
//已知树的后序与中序，求层序遍历;
using namespace std;
const int maxn=1000;
int ho[maxn],mi[maxn];

struct node{
    int l,r;
};
node a[maxn];
int build(int la,int ra,int lb,int rb)
{        //a:中序遍历的左右边界值,b:后序遍历的左右边界值;
    if(la>ra)
        return 0;
    int root,p1,p2;
    root=ho[rb];    //根节点的值为后序遍历的右边界
    p1=la;          //p1指向中序的左边界;
    while(mi[p1]!=root)p1++;//从中序遍历中查找根节点的位置;
    p2=p1-la;       //该根结点的左右子树的结点个数
    a[root].l=build(la,p1-1,lb,lb+p2-1);//递归建树;
    a[root].r=build(p1+1,ra,lb+p2,rb-1);
    return root;
}
void bfs(int x)
{
    queue<int> qq;
    vector<int> vv;
    qq.push(x);
    while(!qq.empty())
    {
        int tmp=qq.front();//取队首元素;
        qq.pop();
        if(tmp==0)
            return ;
        vv.push_back(tmp);//层序遍历;
        if(a[tmp].l!=0)   //根节点的左子树不为空,入队列
            qq.push(a[tmp].l);
        if(a[tmp].r!=0)   //根节点的右子树不为空，入队列
            qq.push(a[tmp].r);
    }
    int len=vv.size();
    for(int i=0;i<len;i++)
        printf("%d%c",vv[i],i==len-1? '\n':' ');//三目运算决定回车或空格;
}
int main()
{
    int n;
    cin >> n;
    for(int i=0;i<n;i++)
        cin >> ho[i];
    for(int i=0;i<n;i++)
        cin >> mi[i];
    build(0,n-1,0,n-1);
    int root=ho[n-1];
    bfs(root);
    return 0;
}
//在先序或后序中，只要我们知道了左子树或者右子树的范围，我们就可以找到根节点的值，
//从而在中序中找到根节点的位置，然后递归去做同样的步骤就好。

二、L2-011. 玩转二叉树

给定一棵二叉树的中序遍历和前序遍历，请你先将树做个镜面反转，再输出反转后的层序遍历的序列。所谓镜面反转，是指将所有非叶结点的左右孩子对换。这里假设键值都是互不相等的正整数。

输入格式：

输入第一行给出一个正整数N（<=30），是二叉树中结点的个数。第二行给出其中序遍历序列。第三行给出其前序遍历序列。数字间以空格分隔。

输出格式：

在一行中输出该树反转后的层序遍历的序列。数字间以1个空格分隔，行首尾不得有多余空格。

输入样例：

7
1 2 3 4 5 6 7
4 1 3 2 6 5 7

输出样例：

4 6 1 7 5 3 2

#include <iostream>
#include <queue>
#include <vector>
#include <cstdio>
using namespace std;
const int maxn=1000;
int mi[maxn],qi[maxn];
struct node{
    int l,r;
}a[maxn];
int build(int la,int ra,int lb,int rb)
{           //中，前;
    if(la>ra)
        return 0;
    int root,p1,p2;
    root=qi[lb];        //根节点为前序编历的左边界;
    p1=la;
    while(mi[p1]!=root)p1++;//在中序遍历中查找根结点；
    p2=p1-la;           //根节点左右子树的个数;
    a[root].l=build(la,p1-1,lb+1,lb+p2);
    a[root].r=build(p1+1,ra,lb+p2+1,rb);
    return root;
}
void bfs(int x)
{
    queue<int> p;
    vector<int> v;
    p.push(x);
    while(!p.empty())
    {
        int tmp=p.front();
        p.pop();
        if(tmp==0)
            return;
        v.push_back(tmp);
        if(a[tmp].r)
            p.push(a[tmp].r);
        if(a[tmp].l)
            p.push(a[tmp].l);
    }
    int len=v.size();
    for(int i=0;i<len;i++)
        printf("%d%c",v[i],i==len-1?'\n':' ');
}
int main()
{
    int n;
    cin >> n;
    for(int i=0;i<n;i++)
        cin >> mi[i];
    for(int i=0;i<n;i++)
        cin >> qi[i];
    build(0,n-1,0,n-1);
    int root=qi[0];
    bfs(root);
    return 0;
}

 

三、Binary Tree Traversals（hdu1710）

Problem Description

A binary tree is a finite set of vertices that is either empty or consists of a root r and two disjoint binary trees called the left and right subtrees. There are three most important ways in which the vertices of a binary tree can be systematically traversed or ordered. They are preorder, inorder and postorder. Let T be a binary tree with root r and subtrees T1,T2.

In a preorder traversal of the vertices of T, we visit the root r followed by visiting the vertices of T1 in preorder, then the vertices of T2 in preorder.

In an inorder traversal of the vertices of T, we visit the vertices of T1 in inorder, then the root r, followed by the vertices of T2 in inorder.

In a postorder traversal of the vertices of T, we visit the vertices of T1 in postorder, then the vertices of T2 in postorder and finally we visit r.

Now you are given the preorder sequence and inorder sequence of a certain binary tree. Try to find out its postorder sequence.

 

 

Input

The input contains several test cases. The first line of each test case contains a single integer n (1<=n<=1000), the number of vertices of the binary tree. Followed by two lines, respectively indicating the preorder sequence and inorder sequence. You can assume they are always correspond to a exclusive binary tree.

 

 

Output

For each test case print a single line specifying the corresponding postorder sequence.

 

 

Sample Input

9 1 2 4 7 3 5 8 9 6 4 7 2 1 8 5 9 3 6

 

 

Sample Output

7 4 2 8 9 5 6 3 1

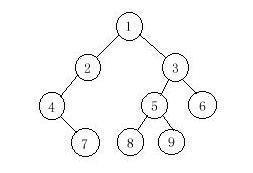
#include <iostream>
#include <vector>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=1005;
int qi[maxn],mi[maxn];
vector<int> pp;
struct node{
    int l,r;
}a[maxn];
int build(int la,int ra,int lb,int rb)//根据前序中序建树;
{   //前，中;
    if(la>ra)
        return 0;
    int root=qi[la],p1=lb,p2;//root为每次前序遍历的根节点;
    while(mi[p1]!=root)p1++;
    p2=p1-lb;               //中序遍历中左子树的结点个数;
    a[root].l=build(la+1,la+p2,lb,p1-1);
    a[root].r=build(la+p2+1,ra,p1+1,rb);
    pp.push_back(root);     //存后序遍历顺序;
    return root;
}
int main()
{
    int n;
    while(cin >> n)
    {
        memset(a,0,sizeof(a));
        for(int i=0;i<n;i++)
            cin >> qi[i];
        for(int i=0;i<n;i++)
            cin >> mi[i];
        build(0,n-1,0,n-1);
        int len=pp.size();
        for(int i=0;i<len;i++)
            printf("%d%c",pp[i],i==n-1?'\n':' ');
        pp.clear();
    }
    return 0;
}

PS：那个动态数组存后序遍历是看网上别人这么写的，自己想的可能就是，建树完再写一个后序遍历函数，虽然感觉自己好像明白这里为什么这样写，但是总感觉没有掌握好= =，多敲敲= =|| ；

这第二个AC代码是我，敲完POJ225收到的启发，敲的；

#include <iostream>
#include <vector>
#include <cstdio>
using namespace std;
const int maxn=1005;
int pre[maxn],mi[maxn];
int pid;        //记录前序遍历中根节点的位置;
vector<int> v;
void pos(int l ,int r)
{
    int i=l;
    while(mi[i]!=pre[pid])i++;
    if(i>l){pid++;pos(l,i-1);}
    if(i<r){pid++;pos(i+1,r);}
    v.push_back(mi[i]);
}
int main()
{
    int n;
    while(cin >> n)
    {
        pid=0;
        for(int i=0;i<n;i++)
            cin >> pre[i];
        for(int i=0;i<n;i++)
            cin >> mi[i];
        pos(0,n-1);
        for(int i=0;i<n;i++)
            printf("%d%c",v[i],i==n-1?'\n':' ');
        v.clear();
    }
    return 0;
}

 

四、Tree Recovery（POJ2255）

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 16175		Accepted: 9968

Description

Little Valentine liked playing with binary trees very much. Her favorite game was constructing randomly looking binary trees with capital letters in the nodes. 
This is an example of one of her creations: 

                                               D

                                              / \

                                             /   \

                                            B     E

                                           / \     \

                                          /   \     \

                                         A     C     G

                                                    /

                                                   /

                                                  F

To record her trees for future generations, she wrote down two strings for each tree: a preorder traversal (root, left subtree, right subtree) and an inorder traversal (left subtree, root, right subtree). For the tree drawn above the preorder traversal is DBACEGF and the inorder traversal is ABCDEFG. 
She thought that such a pair of strings would give enough information to reconstruct the tree later (but she never tried it). 

Now, years later, looking again at the strings, she realized that reconstructing the trees was indeed possible, but only because she never had used the same letter twice in the same tree. 
However, doing the reconstruction by hand, soon turned out to be tedious. 
So now she asks you to write a program that does the job for her! 

Input

The input will contain one or more test cases. 
Each test case consists of one line containing two strings preord and inord, representing the preorder traversal and inorder traversal of a binary tree. Both strings consist of unique capital letters. (Thus they are not longer than 26 characters.) 
Input is terminated by end of file. 

Output

For each test case, recover Valentine's binary tree and print one line containing the tree's postorder traversal (left subtree, right subtree, root).

Sample Input

DBACEGF ABCDEFG
BCAD CBAD

Sample Output

ACBFGED
CDAB

#include <iostream>

using namespace std;

string a,b;
int pid;//记录前序中根节点的位置;

void pos(int l,int r)
{       //参数：中序遍历的左右边界;
    int i=l;
    while(b[i]!=a[pid])i++;     //在中序中查找根节点;
    if(i>l){pid++;pos(l,i-1);}  //递遍历左子树--i的初始值为l，如果i已为根节点，则上一步不会++，这一步就不会执行;
    if(i<r){pid++;pos(i+1,r);}  //递归遍历右子树;
    cout << b[i];
}
int main()
{
    while(cin >> a >> b)
    {
        pid=0;
        pos(0,b.size()-1);
        cout << endl;
    }
    return 0;
}
//在中序遍历中查找根节点;

PS：看题解敲的= =。。。

五、L2-004. 这是二叉搜索树吗？

一棵二叉搜索树可被递归地定义为具有下列性质的二叉树：对于任一结点，

• 其左子树中所有结点的键值小于该结点的键值；
• 其右子树中所有结点的键值大于等于该结点的键值；
• 其左右子树都是二叉搜索树。

所谓二叉搜索树的“镜像”，即将所有结点的左右子树对换位置后所得到的树。

给定一个整数键值序列，现请你编写程序，判断这是否是对一棵二叉搜索树或其镜像进行前序遍历的结果。

输入格式：

输入的第一行给出正整数N（<=1000）。随后一行给出N个整数键值，其间以空格分隔。

输出格式：

如果输入序列是对一棵二叉搜索树或其镜像进行前序遍历的结果，则首先在一行中输出“YES”，然后在下一行输出该树后序遍历的结果。数字间有1个空格，一行的首尾不得有多余空格。若答案是否，则输出“NO”。

输入样例1：

7
8 6 5 7 10 8 11

输出样例1：

YES
5 7 6 8 11 10 8

输入样例2：

7
8 10 11 8 6 7 5

输出样例2：

YES
11 8 10 7 5 6 8

输入样例3：

7
8 6 8 5 10 9 11

输出样例3：

NO

 

#include <iostream>
#include <cstdio>
#include <vector>

using namespace std;
bool flag=false;
vector<int> pre;
vector<int> pos;
void getpos(int root,int tail)
{
    if(root>tail)return;
    int i=root+1,j=tail;//i,j为根节点后的区间左右边界;
    if(!flag)
    {
        while(i<=tail&&pre[root]>pre[i])i++;//从左查找第一个大于等于根节点的位置
        while(j>root&&pre[root]<=pre[j])j--;//从右查找第一个小于根节点的位置
    }else{
        while(i<=tail&&pre[root]<=pre[i])i++;//镜像
        while(j>root&&pre[root]>pre[j])j--;
    }
    if(i-j!=1)return;   //不符合
    getpos(root+1,j);   //递归判断左子树
    getpos(i,tail);     //递归判断右子树
    pos.push_back(pre[root]);
}
int main()
{
    int n;
    cin >> n;
    //pre.resize(n);//不加这个预先分配空间，就运行不了;
    for(int i=0;i<n;i++)
    {
        int tmp;
        //cin >> pre[i];
        cin >> tmp;
        pre.push_back(tmp);
    }
    getpos(0,n-1);      //对二叉树进行判断
    if(pos.size()!=n)   //不符合，再对其镜像判断
    {
        flag=true;
        pos.clear();
        getpos(0,n-1);
    }
    if(pos.size()==n)  //
    {
            cout << "YES" << endl;
        for(int i=0;i<n;i++)
            printf("%d%c",pos[i],i==n-1?'\n':' ');
    }else
        cout << "NO" << endl;
    return 0;
}
//给你一颗树的前序遍历，判断其是否是二叉搜索树或其镜像，是则输出其后序遍历;

PS，找的最简洁的代码了，理解起来很简单，但是不知道自己能不能敲好，递归的运用感觉自己并没有尝试过= =；

六、The order of a Tree（hdu3999）

Problem Description

As we know,the shape of a binary search tree is greatly related to the order of keys we insert. To be precisely:
1.  insert a key k to a empty tree, then the tree become a tree with
only one node;
2.  insert a key k to a nonempty tree, if k is less than the root ,insert
it to the left sub-tree;else insert k to the right sub-tree.
We call the order of keys we insert “the order of a tree”,your task is,given a oder of a tree, find the order of a tree with the least lexicographic order that generate the same tree.Two trees are the same if and only if they have the same shape.

 

Input

There are multiple test cases in an input file. The first line of each testcase is an integer n(n <= 100,000),represent the number of nodes.The second line has n intergers,k1 to kn,represent the order of a tree.To make if more simple, k1 to kn is a sequence of 1 to n.

 

Output

One line with n intergers, which are the order of a tree that generate the same tree with the least lexicographic.

 

Sample Input

4 1 3 4 2

 

Sample Output

1 3 2 4

 

Source

2011 Multi-University Training Contest 16 - Host by TJU

题意：给一段建树顺序，建一棵二叉搜索树，并输这个BST的前序遍历顺序;

 

 七、BST（POJ2309）

Time Limit: 1000MS   Memory Limit: 65536K Total Submissions: 10503   Accepted: 6427 Description Consider an infinite full binary search tree (see the figure below), the numbers in the nodes are 1, 2, 3, .... In a subtree whose root node is X, we can get the minimum number in this subtree by repeating going down the left node until the last level, and we can also find the maximum number by going down the right node. Now you are given some queries as "What are the minimum and maximum numbers in the subtree whose root node is X?" Please try to find answers for there queries.  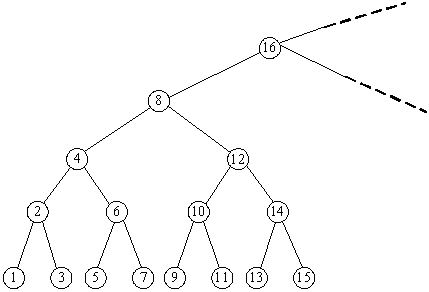Input In the input, the first line contains an integer N, which represents the number of queries. In the next N lines, each contains a number representing a subtree with root number X (1 <= X <= 2 31 - 1). Output There are N lines in total, the i-th of which contains the answer for the i-th query. Sample Input 2 8 10 Sample Output 1 15 9 11 Source POJ Monthly,Minkerui

这里的位运算用了树状数组中的lowbit，这是表示数x的二进制表示的最右端的1，计算机程序中整数采用补码表示，-x为x按位取反，末尾加1以后的结果，按位与后的结果就是所有位都变成了0，除了lowbit的1；在这题中，这个k值表示x除2的k次方后为奇数2^k=lowbit（x）,(这里为什么是这样计算的，可以参考十进制转换为二进制的过程，就能明白了）；

#include <iostream>
#include <cmath>
using namespace std;
/*BST*/
int lowbit(int x)
{
    return x&(-x);
}
int main()
{
    int n;
    cin >> n;
    while(n--){
        int a;
        cin >> a;
        cout << a-lowbit(a)+1 << " " << a+lowbit(a)-1 <<endl;
    }
    return 0;
}

 二叉堆（heap）

 哈夫曼树

 

转载于:https://www.cnblogs.com/Cloud-king/p/8733117.html