http://blog.jobbole.com/67588/
【编注】:动态规划(Dynamic programming)是一种在数学、计算机科学和经济学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。 动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。
动态规划背后的基本思想非常简单。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再合并子问题的解以得出原问题的解。 通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量: 一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。 这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。—— 维基百科
动态规划是一种用来解决定义了一个状态空间的问题的算法策略。这些问题可分解为新的子问题,子问题有自己的参数。为了解决它们,我们必须搜索这个状态空间并且在每一步作决策时进行求值。得益于这类问题会有大量相同的状态的这个事实,这种技术不会在解决重叠的子问题上浪费时间。
正如我们看到的,它也会导致大量地使用递归,这通常会很有趣。
为了说明这种算法策略,我会用一个很好玩的问题来作为例子,这个问题是我最近参加的 一个编程竞赛中的 Tuenti Challenge #4 中的第 14 个挑战问题。
Train Empire
我们面对的是一个叫 Train Empire 的棋盘游戏(Board Game)。在这个问题中,你必须为火车规划出一条最高效的路线来运输在每个火车站的货车。规则很简单:
- 每个车站都有一个在等待着的将要运送到其他的车站的货车。
- 每个货车被送到了目的地会奖励玩家一些分数。货车可以放在任意车站。
- 火车只在一条单一的路线上运行,每次能装一个货车,因为燃料有限只能移动一定的距离。
我们可以把我们的问题原先的图美化一下。为了在燃料限制下赢得最大的分数,我们需要知道货车在哪里装载,以及在哪里卸载。
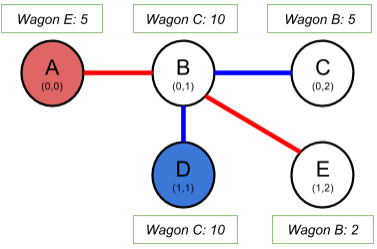
我们在图片中可以看到,我们有两条火车路线:红色和蓝色。车站位于某些坐标点上,所以我们很容易就能算出它们之间的距离。每一个车站有一个以它的终点命名的货车,以及当我们成功送达它可以得到的分数奖励。
现在,假定我们的货车能跑3千米远。红色路线上的火车可以把 A 车站的火车送到它的 终点 E (5点分数),蓝色路线上的火车可以运送货车 C(10点分数),然后运送货车 B(5点分数)。 可以取得最高分20分。
状态表示
我们把火车的位置,以及火车所走的距离和每个车站的货车表格叫做一个问题状态。 改变这些值我们得到的仍是相同的问题,但是参数变了。我们可以看到每次我们移动 一列火车,我们的问题就演变到一个不同的子问题。为了算出最佳的移动方案,我们 必须遍历这些状态然后基于这些状态作出决策。让我们开始把。
我们将从定义火车路线开始。因为这些路线不是直线,所以图是最好的表示方法。
Python
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | import math from decimal import Decimal from collections import namedtuple, defaultdict
class TrainRoute:
def __init__(self, start, connections): self.start = start
self.E = defaultdict(set) self.stations = set() for u, v in connections: self.E[u].add(v) self.E[v].add(u) self.stations.add(u) self.stations.add(v)
def next_stations(self, u): if u not in self.E: return yield from self.E[u]
def fuel(self, u, v): x = abs(u.pos[0] - v.pos[0]) y = abs(u.pos[1] - v.pos[1]) return Decimal(math.sqrt(x * x + y * y)) |
TrainRoute 类实现了一个非常基本的有向图,它把顶点作为车站存在一个集合中,把车站间 的连接存在一个字典中。请注意我们把 (u, v) 和 (v, u) 两条边都加上了,因为火车可以 向前向后移动。
在 next_stations 方法中有一个有趣东西,在这里我使用了一个很酷的 Python 3 的特性 yield from。这允许一个生成器 可以委派到另外一个生成器或者迭代器中。因为每一个车站都映射到一个车站的集合,我们只 需要迭代它就可以了。
让我们来看一下 main class:
Python
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | TrainWagon = namedtuple('TrainWagon', ('dest', 'value')) TrainStation = namedtuple('TrainStation', ('name', 'pos', 'wagons'))
class TrainEmpire:
def __init__(self, fuel, stations, routes): self.fuel = fuel self.stations = self._build_stations(stations) self.routes = self._build_routes(routes)
def _build_stations(self, station_lines): # ...
def _build_routes(self, route_lines): # ...
def maximum_route_score(self, route):
def score(state): return sum(w.value for (w, s) in state.wgs if w.dest == s.name)
def wagon_choices(state, t): # ...
def delivered(state): # ...
def next_states(state): # ...
def backtrack(state): # ...
# ...
def maximum_score(self): return sum(self.maximum_route_score(r) for r in self.routes) |
我省略了一些代码,但是我们可以看到一些有趣的东西。两个 命名元组 将会帮助保持我们的数据整齐而简单。main class 有我们的火车能够运行的最长的距离,燃料, 和路线以及车站这些参数。maximum_score 方法计算每条路线的分数的总和,将成为解决问题的 接口,所以我们有:
- 一个 main class 持有路线和车站之间的连接
- 一个车站元组,存有名字,位置和当前存在的货车列表
- 一个带有一个值和目的车站的货车
动态规划
我已经尝试解释了动态规划如何高效地搜索状态空间的关键,以及基于已有的状态进行最优的决策。 我们有一个定义了火车的位置,火车剩余的燃料,以及每个货车的位置的状态空间——所以我们已经可以表示初始状态。
我们现在必须考虑在每个车站的每一种决策。我们应该装载一个货车然后把它送到目的地吗? 如果我们在下一个车站发现了一个更有价值的货车怎么办?我们应该把它送回去或者还是往前 移动?或者还是不带着货车移动?
很显然,这些问题的答案是那个可以使我们获得更多的分数的那个。为了得到答案,我们必须求出 所有可能的情形下的前一个状态和后一个状态的值。当然我们用求分函数 score 来求每个状态的值。
Python
| 1 2 3 4 5 6 7 8 9 10 | def maximum_score(self): return sum(self.maximum_route_score(r) for r in self.routes)
State = namedtuple('State', ('s', 'f', 'wgs'))
wgs = set() for s in route.stations: for w in s.wagons: wgs.add((w, s)) initial = State(route.start, self.fuel, tuple(wgs)) |
从每个状态出发都有几个选择:要么带着货车移动到下一个车站,要么不带货车移动。停留不动不会进入一个新的 状态,因为什么东西都没改变。如果当前的车站有多个货车,移动它们中的一个都将会进入一个不同的状态。
Python
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | def wagon_choices(state, t): yield state.wgs # not moving wagons is an option too
wgs = set(state.wgs) other_wagons = {(w, s) for (w, s) in wgs if s != state.s} state_wagons = wgs - other_wagons for (w, s) in state_wagons: parked = state_wagons - {(w, s)} twgs = other_wagons | parked | {(w, t)} yield tuple(twgs)
def delivered(state): return all(w.dest == s.name for (w, s) in state.wgs)
def next_states(state): if delivered(state): return for s in route.next_stations(state.s): f = state.f - route.fuel(state.s, s) if f < 0: continue for wgs in wagon_choices(state, s): yield State(s, f, wgs) |
next_states 是一个以一个状态为参数然后返回所有这个状态能到达的状态的生成器。 注意它是如何在所有的货车都移动到了目的地后停止的,或者它只进入到那些燃料仍然足够的状态。wagon_choices 函数可能看起来有点复杂,其实它仅仅返回那些可以从当前车站到下一个车站的货车集合。
这样我们就有了实现动态规划算法需要的所有东西。我们从初始状态开始搜索我们的决策,然后选择 一个最有策略。看!初始状态将会演变到一个不同的状态,这个状态也会演变到一个不同的状态! 我们正在设计的是一个递归算法:
- 获取状态
- 计算我们的决策
- 做出最优决策
显然每个下一个状态都将做这一系列的同样的事情。我们的递归函数将会在燃料用尽或者所有的货车都被运送都目的地了时停止。
Python
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | max_score = {}
def backtrack(state): if state.f <= 0: return state choices = [] for s in next_states(state): if s not in max_score: max_score[s] = backtrack(s) choices.append(max_score[s]) if not choices: return state return max(choices, key=lambda s: score(s))
max_score[initial] = backtrack(initial) return score(max_score[initial]) |
完成动态规划策略的最后一个陷阱:在代码中,你可以看到我使用了一个 max_score 字典, 它实际上缓存着算法经历的每一个状态。这样我们就不会重复一遍又一遍地遍历我们的我们早就已经 经历过的状态的决策。
当我们搜索状态空间的时候,一个车站可能会到达多次,这其中的一些可能会导致相同的燃料,相同的货车。 火车怎么到达这里的没关系,只有在那个时候做的决策有影响。如果我们我们计算过那个状态一次并且保存了 结果,我们就不在需要再搜索一遍这个子空间了。
如果我们没有用这种记忆化技术,我们会做大量完全相同的搜索。 这通常会导致我们的算法很难高效地解决我们的问题。
总结
Train Empire 提供了一个绝佳的的例子,以展示动态规划是如何在有重叠子问题的问题做出最优决策。 Python 强大的表达能力再一次让我们很简单地就能把想法实现,并且写出清晰且高效的算法。
完整的代码在 contest repository。
五种常用算法之三:动态规划
动态规划
基本思想:
动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样,但它们具有相同的填表格式。
与分治法最大的差别是:适合于用动态规划法求解的问题,经分解后得到的子问题往往不是互相独立的(即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解)
应用场景:
适用动态规划的问题必须满足最优化原理、无后效性和重叠性。
1.最优化原理(最优子结构性质) 最优化原理可这样阐述:一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。简而言之,一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。
2.无后效性 将各阶段按照一定的次序排列好之后,对于某个给定的阶段状态,它以前各阶段的状态无法直接影响它未来的决策,而只能通过当前的这个状态。换句话说,每个状态都是过去历史的一个完整总结。这就是无后向性,又称为无后效性。
3.子问题的重叠性 动态规划将原来具有指数级时间复杂度的搜索算法改进成了具有多项式时间复杂度的算法。其中的关键在于解决冗余,这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种状态,所以它的空间复杂度要大于其它的算法。
求全路径最短路径的Floyd算法就是漂亮地运用了动态规划思想。
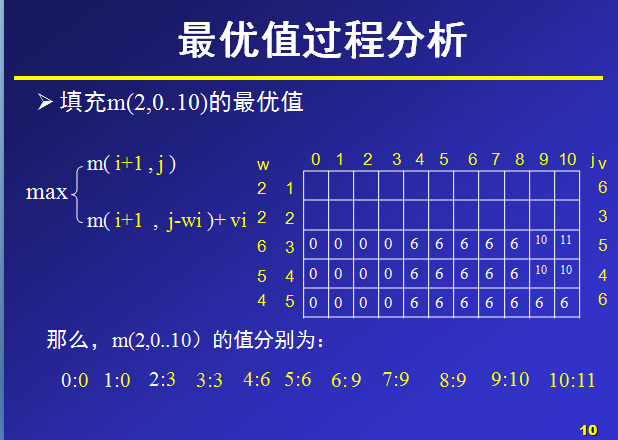
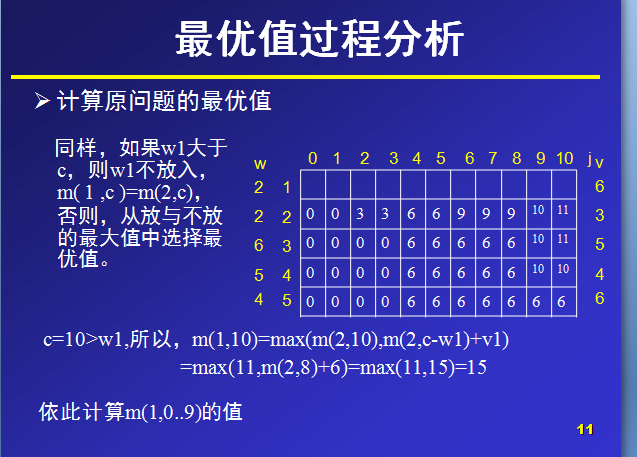
下面是我找到的一个关于 0-1背包问题 的动态规划思想PPT截图:
问题描述:
给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为C。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
对于一种物品,要么装入背包,要么不装。所以对于一种物品的装入状态可以取0和1.我们设物品i的装入状态为xi,xi∈ (0,1),此问题称为0-11背包问题。
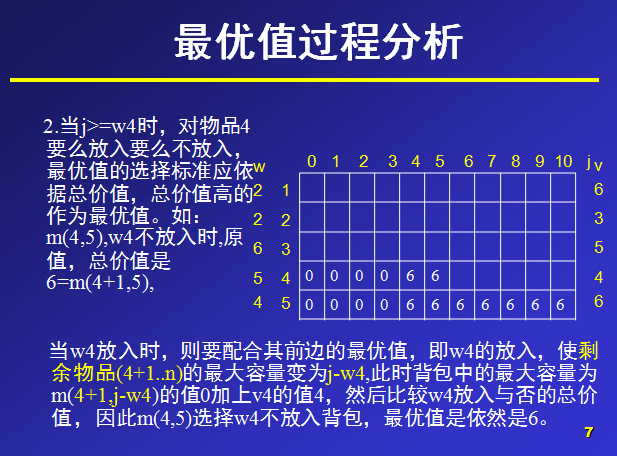
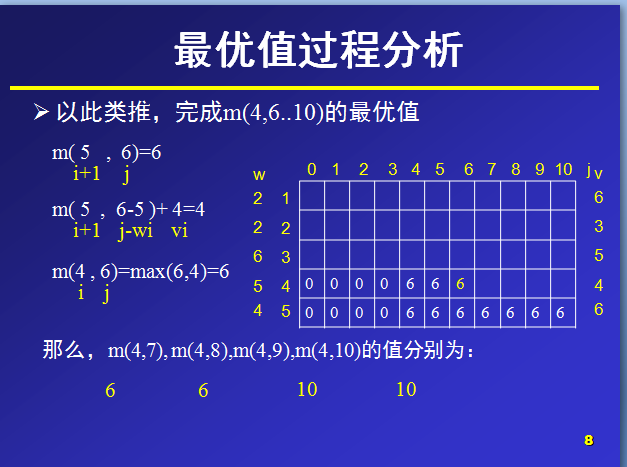
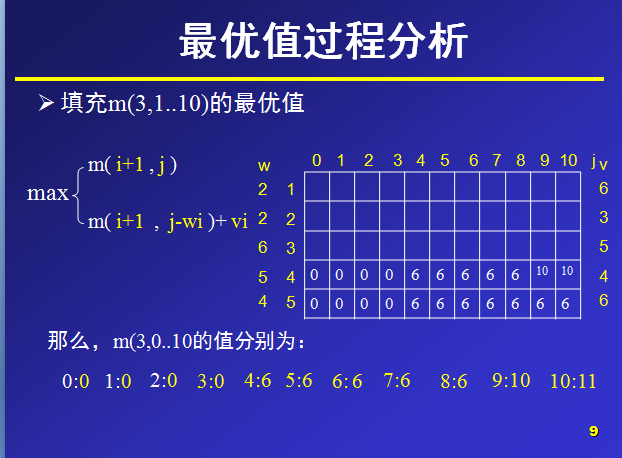
数据:物品个数n=5,物品重量w[n]={0,2,2,6,5,4},物品价值V[n]={0,6,3,5,4,6},
(第0位,置为0,不参与计算,只是便于与后面的下标进行统一,无特别用处,也可不这么处理。)总重量c=10。背包的最大容量为10,那么在设置数组m大小时,可以设行列值为6和11,那么,对于m(i,j)就表示可选物品为i…n背包容量为j(总重量)时背包中所放物品的最大价值。































 153
153











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








