分布直方图分析概率_55道题目，176多张图片，31种题型，带你认知高考概率题型内容...

55道题目，176多张图片，31种题型，带你认知高考概率题型内容

55道题目，176多张图片，31种题型，带你认知高考概率题型内容

本题主要考查系统抽样.

本题考查抽样数据的统计，渗透了数据处理和数学运算素养．采取去重法，利用转化与化归思想解题．

众数：一组数据出现次数最多的数叫众数，众数反映一组数据的多数水平；

中位数：一组数据中间的数(起到分水岭的作用)，中位数反映一组数据的中间水平；

平均数：反映一组数据的平均水平；

方差：反映一组数据偏离平均数的程度，用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)．在样本容量相同的情况下，方差越大，说明数据的波动越大，越不稳定．

标准差是方差的算术平方根，意义在于反映一组数据的离散程度．

本题旨在考查学生对中位数、平均数、方差、极差本质的理解.

该题考查的是有关新农村建设前后的经济收入的构成比例的饼形图，要会从图中读出相应的信息即可得结果.

本题主要考查统计知识及对学生柱形图的理解

由折线图，7月份后月接待游客量减少，A错误；本题选择A选项.

解答本题时易错可能有两种：(1)对图形中的线条认识不明确，不知所措，只觉得是两把雨伞重叠在一起，找不到解决问题的方法；(2)估计平均温差时易出现错误，错选B．

作为客观题形式出现的古典概型试题,一般难度不大,解答中的常见错误是在用列举法计数时出现重复或遗漏,避免此类错误发生的有效方法是按照一定的标准进行列举.

应用古典概型求某事件的步骤：第一步，判断本试验的结果是否为等可能事件，设出事件；第二步，分别求出基本事件的总数与所求事件中所包含的基本事件个数；第三步，利用公式求出事件的概率.

本题主要考查古典概率的求解，题目较易，注重了基础知识、基本计算能力的考查．应用列举法写出所有基本事件过程中易于出现遗漏或重复，将兔子标注字母，利用“树图法”，可最大限度的避免出错．

对古典概型必须明确两点：①对于每个随机试验来说，试验中所有可能出现的基本事件只有有限个；②每个基本事件出现的可能性相等．只有在同时满足①、②的条件下，运用的古典概型计算公式得出的结果．

本题主要考查事件的基本关系和概率的计算，属于基础题．

对于几何概型的计算，首先确定事件类型为几何概型并确定其几何区域(长度、面积、体积或时间)，其次计算基本事件区域的几何度量和事件A区域的几何度量，最后计算.

该题考查的是面积型几何概型的有关问题，题中需要解决的是概率的大小，根据面积型几何概型的概率公式，将比较概率的大小问题转化为比较区域的面积的大小，利用相关图形的面积公式求得结果.

对于几何概型的概率公式中的“测度”要有正确的认识，它只与大小有关，而与形状和位置无关，在解题时，要掌握“测度”为长度、面积、体积、角度等常见的几何概型的求解方法．

这是全国卷考查几何概型,求解几何概型问题的关键是确定“测度”,常见的测度有长度、面积、体积等.

本题考点为概率统计，渗透了数据处理和数学运算素养．侧重统计数据的概率估算，难度不大．易忽视概率的估算值不是精确值而失误，根据分类抽样的统计数据，估算出正点列车数量与列车总数的比值．

由于本题题干较长，所以，易错点之一就是能否静心读题，正确理解题意；易错点之二是思维的全面性是否具备，要考虑甲队以获胜的两种情况；易错点之三是是否能够准确计算．

本题考查常见背景中的古典概型，渗透了数学建模和数学运算素养．采取等同法，等价转化的思想解题．

古典概型中基本事件方法：(1)列举法. (2)树状图法：较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目，常采用树状图法. (3)列表法：多元素基本事件的求解问题，通过列表把复杂的题目简单化、抽象的题目具体化. (4)排列组合法：限制条件较多且元素数目较多的题目.

n次独立重复试验．

本题主要考查利用两个计数原理与排列组合计算古典概型问题，渗透了传统文化、数学计算等数学素养，“重卦”中每一爻有两种情况，基本事件计算是住店问题，该重卦恰有3个阳爻是相同元素的排列问题，利用直接法即可计算．对利用排列组合计算古典概型问题，首先要分析元素是否可重复，其次要分析是排列问题还是组合问题．本题是重复元素的排列问题，所以基本事件的计算是“住店”问题，满足条件事件的计算是相同元素的排列问题即为组合问题．

本题考查离散型随机变量的方差的求法，考查二项分布的性质等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．

本题主要考查二项分布相关知识，属于中档题．

本题考查古典概型的相关性质，能否通过题意得出以及所包含的事件是解决本题的关键，考查推理能力，考查学生从题目中获取所需信息的能力，是中档题。

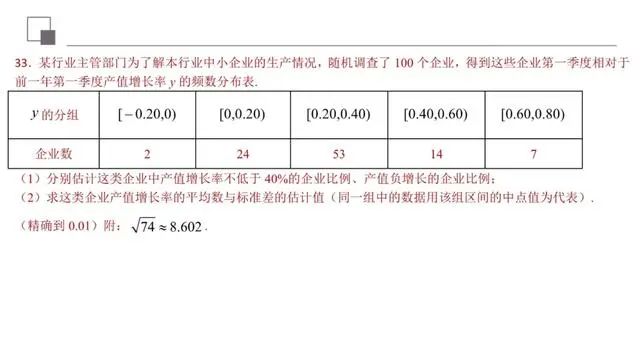
本题考查平均值以及标准差的计算，主要考查平均值以及标准差的计算公式，考查学生从信息题中获取所需信息的能力，考查学生的计算能力，是简单题．

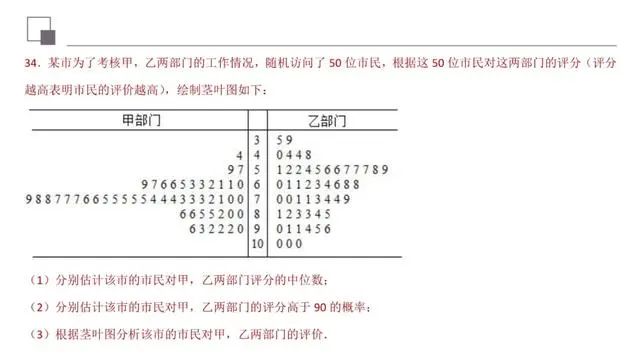
1平均数，古典概型概率；2统计．

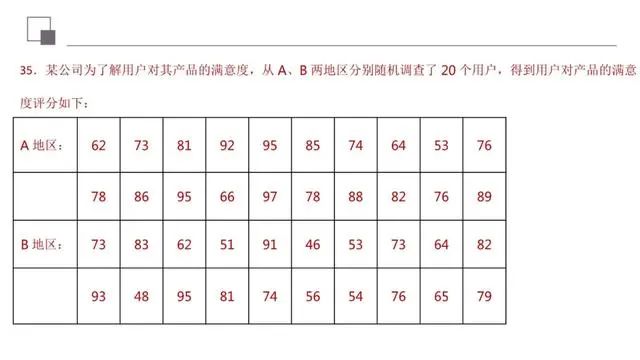
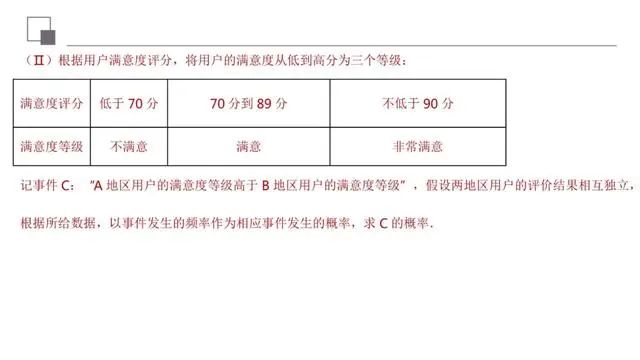
本题考查茎叶图和特征数，求互斥事件和独立事件的概率，关键在于将事件分成相互独立互斥事件，分别求其概率，再运用概率的加法公式，属于基础题．

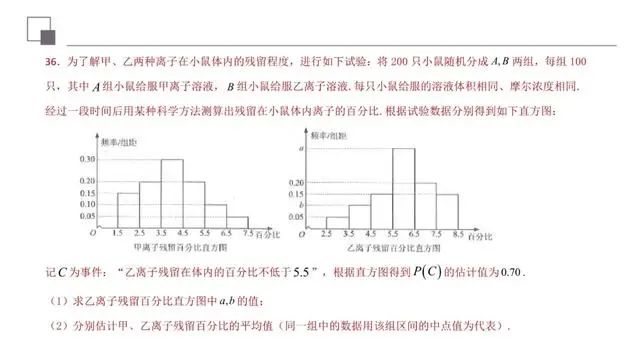
本题考查频率分布直方图和平均数，属于基础题.

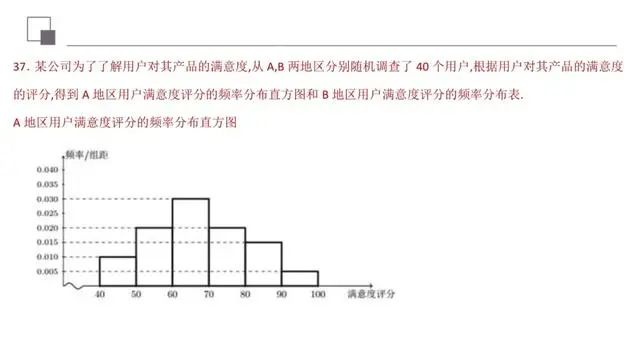
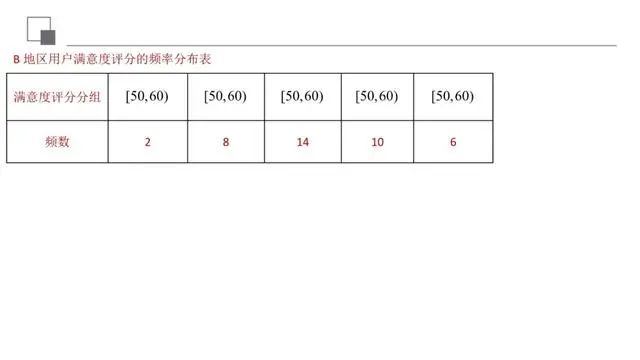
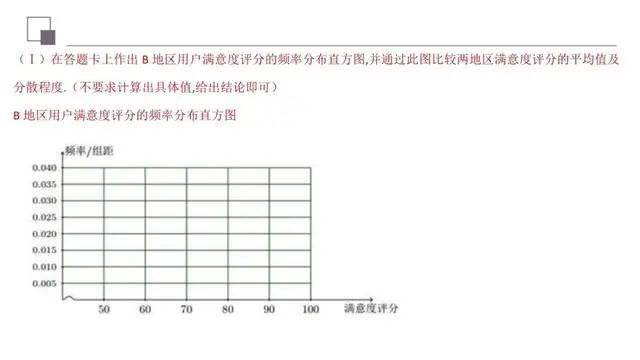
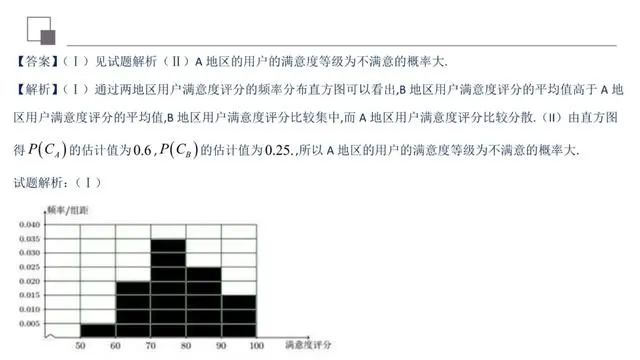
本题主要考查频率分布直方图及概率估计.

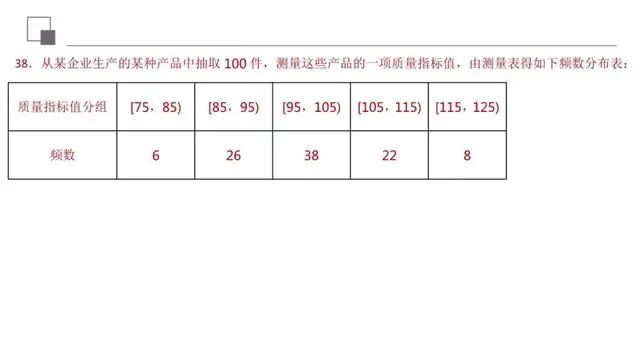
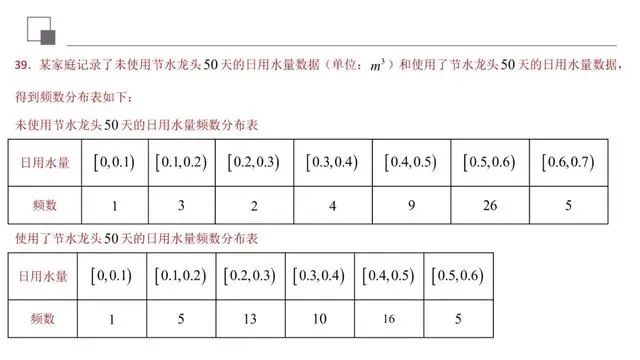
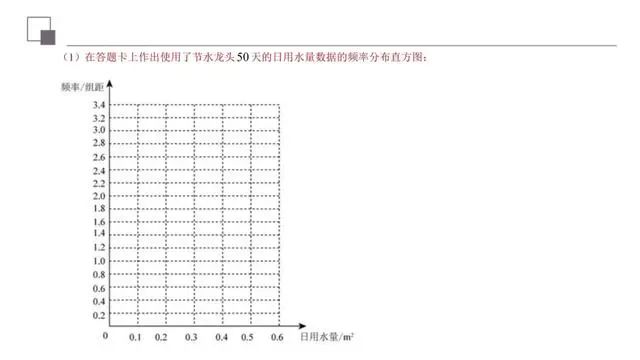
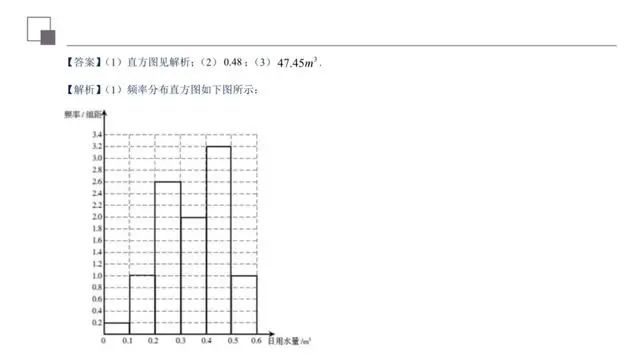
该题考查的是有关统计的问题，涉及到的知识点有频率分布直方图的绘制、利用频率分布直方图计算变量落在相应区间上的概率、利用频率分布直方图求平均数，在解题的过程中，需要认真审题，细心运算，仔细求解，就可以得出正确结果.

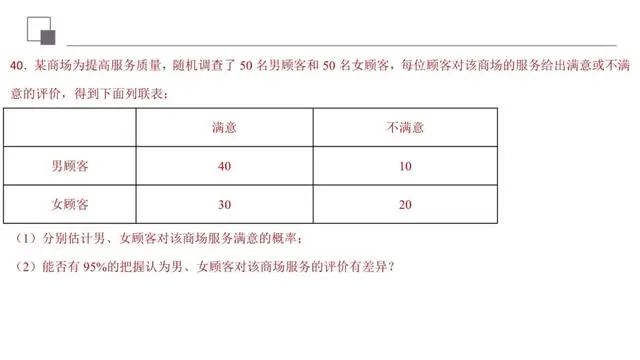
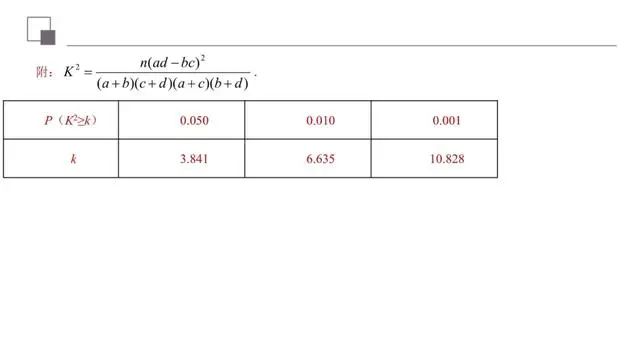
该题考查的是有关概率与统计的知识，涉及到的知识点有利用频率来估计概率，利用列联表计算的值，独立性检验，属于简单题目.

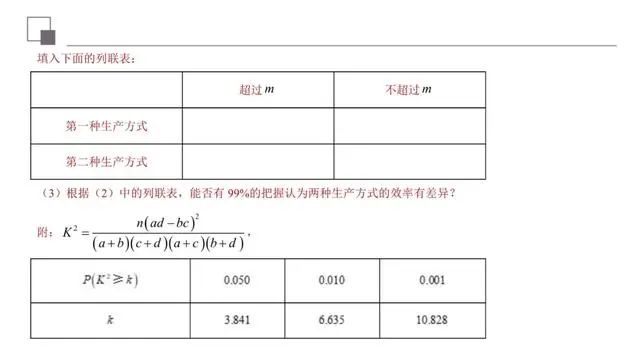
本题主要考查了茎叶图和独立性检验，考察学生的计算能力和分析问题的能力，贴近生活．

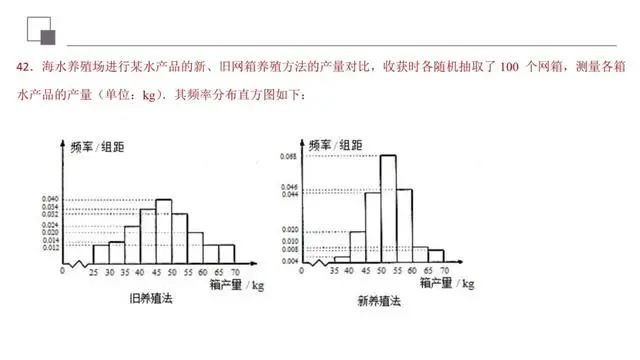
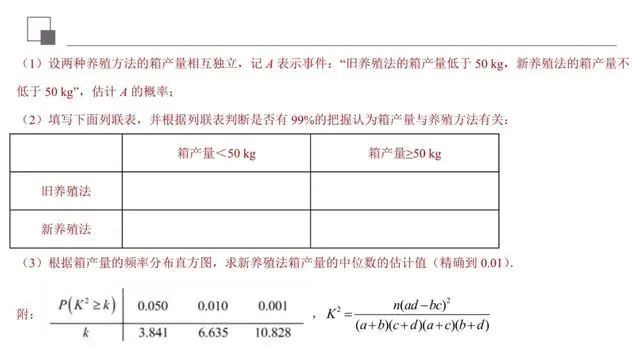
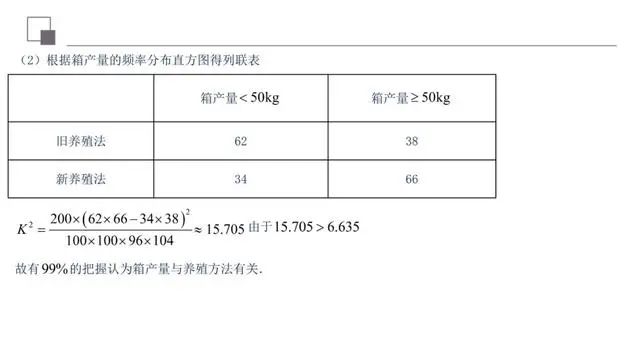
(1)利用独立性检验，能够帮助我们对日常生活中的实际问题作出合理的推断和预测．独立性检验就是考察两个分类变量是否有关系，并能较为准确地给出这种判断的可信度，随机变量的观测值值越大，说明“两个变量有关系”的可能性越大．

(2)利用频率分布直方图求众数、中位数和平均数时，应注意三点：①最高的小长方形底边中点的横坐标即众数；②中位数左边和右边的小长方形的面积和是相等的；③平均数是频率分布直方图的“重心”，等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和．

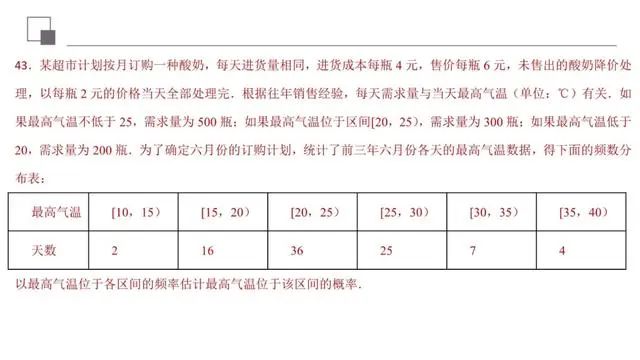
本题考查概率的求法，考查利润的所有可能取值的求法，考查函数、古典概型等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查数形结合思想、化归与转化思想，是中档题．

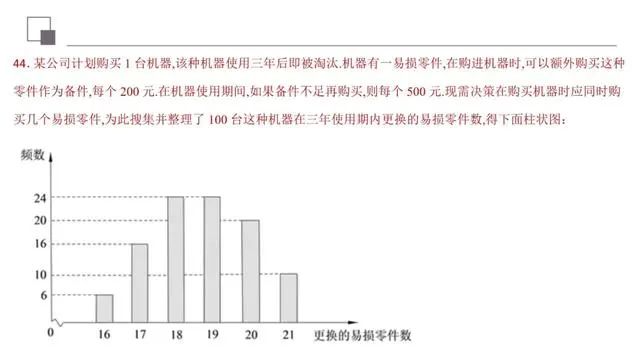
本题把统计与函数结合在一起进行考查,有综合性但难度不大,求解的关键是读懂题意,所以提醒考生要重视数学中的阅读理解问题.

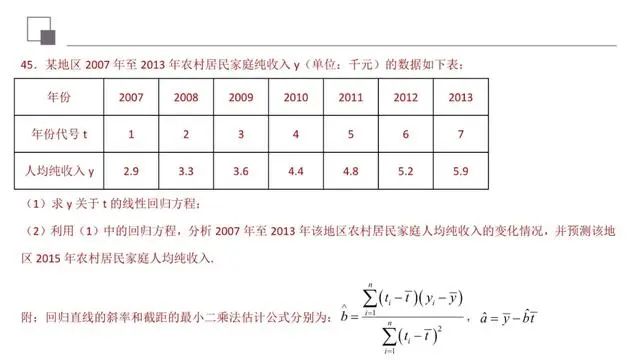
本题主要考查线性回归方程、平均数等基础知识，考查学生的分析问题解决问题的能力、转化能力、计算能力．

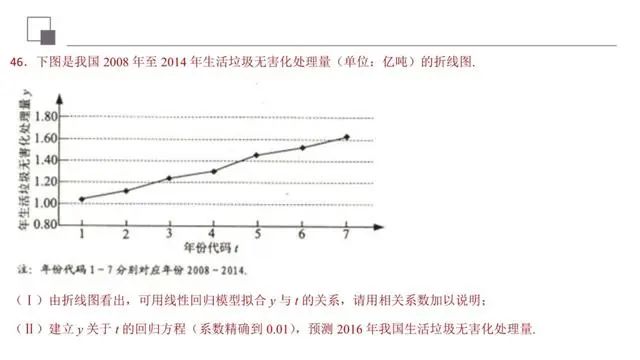
线性相关系数与线性回归方程的求法与应用，(1)判断两个变量是否线性相关及相关程度通常有两种方法：(1)利用散点图直观判断；(2)将相关数据代入相关系数公式求出相关系数，然后根据相关系数的大小进行判断．求线性回归方程时要严格按照公式求解，并一定要注意计算的准确性．

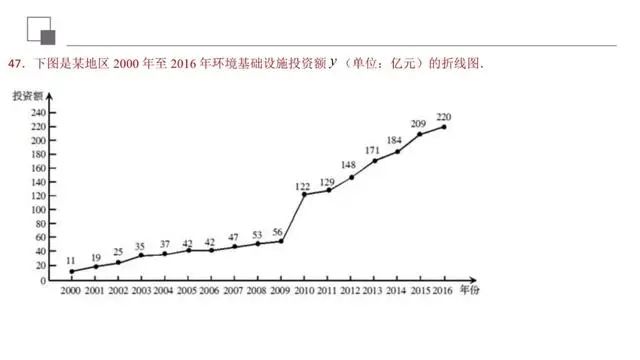
已知回归直线方程，则可以直接将数值代入求得特定要求下的预测值；若回归直线方程有待定参数，则根据回归直线方程恒过点求参数.

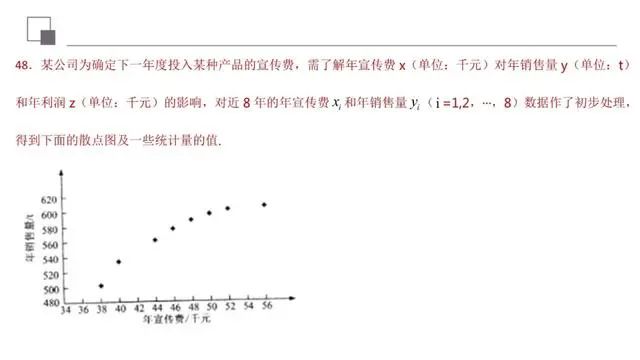
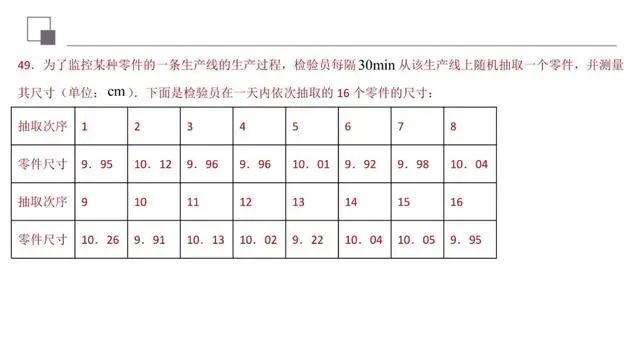
解答新颖的数学题时，一是通过转化，化“新”为“旧”；二是通过深入分析，多方联想，以“旧”攻“新”；三是创造性地运用数学思想方法，以“新”制“新”，应特别关注创新题型的切入点和生长点．

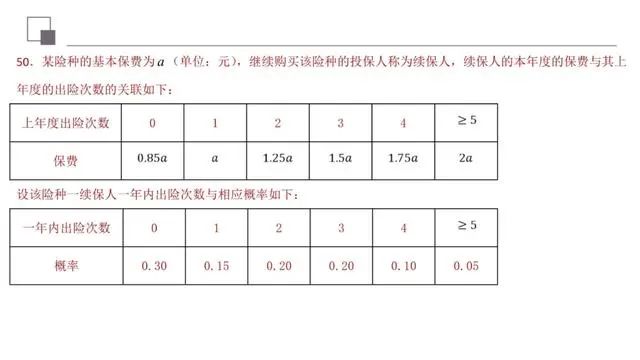
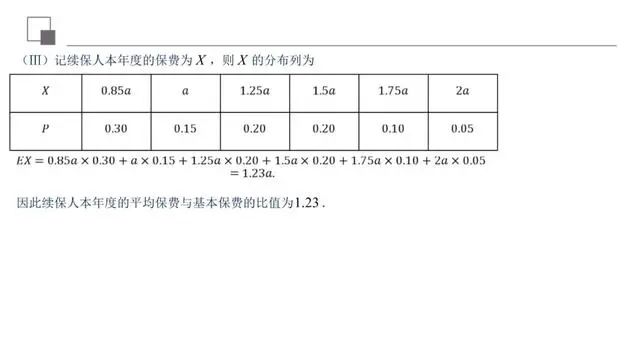
条件概率的求法：(1)定义法：求P(A)和P(AB)，由P(B|A)，求出P(B|A)；(2)基本事件法：当基本事件适合有限性和等可能性时，可借助古典概型概率公式，先求事件A包含的基本事件数n(A)，再在事件A发生的条件下求事件B包含的基本事件数n(AB)，得P(B|A).

离散型随机变量均值的步骤：(1)随机变量X的意义，写出X可能取得的全部值；(2)求X取每个值时的概率；(3)写出X的分布列；(4)由均值定义求出EX．

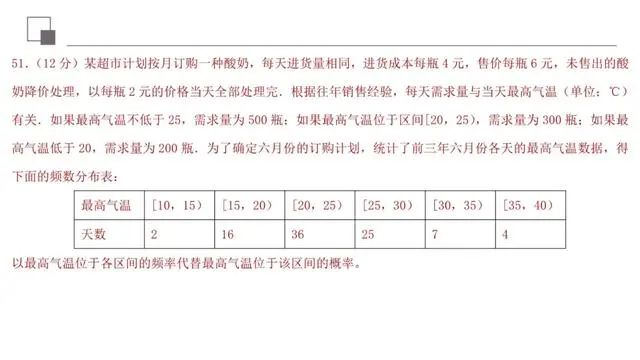
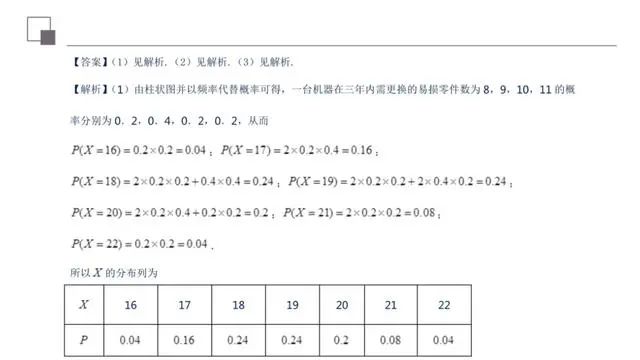
本题考查离散型随机变量分布列的求解、利用递推关系式证明等比数列、累加法求解数列通项公式和数列中的项的问题.本题综合性较强，要求学生能够熟练掌握数列通项求解、概率求解的相关知识，对学生分析和解决问题能力要求较高.

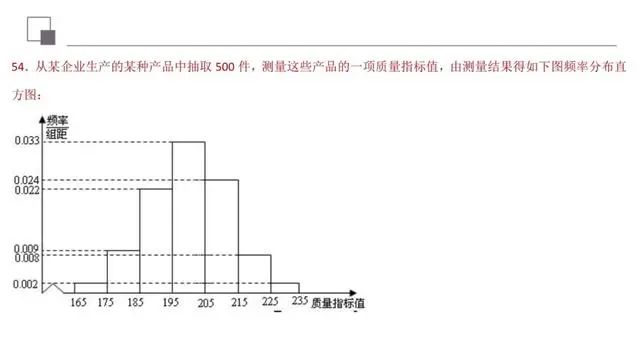
1、频率分布直方图；2、正态分布的原则；3、二项分布的期望．

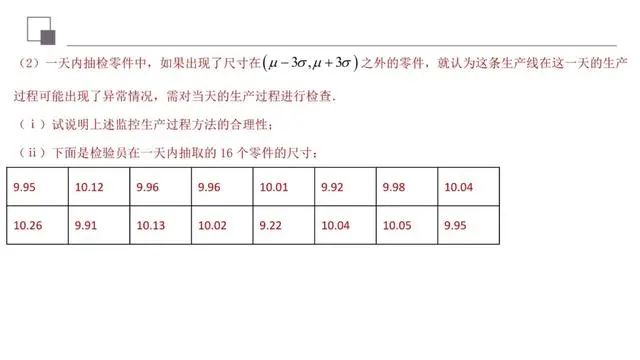
数学期望是离散型随机变量中重要的数学概念，反映随机变量取值的平均水平.求解离散型随机变量的分布列、数学期望时，首先要分清事件的构成与性质，确定离散型随机变量的所有取值，然后根据概率类型选择公式，计算每个变量取每个值的概率，列出对应的分布列，最后求出数学期望.正态分布是一种重要的分布，之前考过一次，尤其是正态分布的原则.