
共轭梯度法是Hestenes和Stiefel(1952年)在求解大规模线性方程组时创立的一种迭代算法。1964年,Fletcher和Reeves将其引入非线性最优化问题,创立了非线性共轭梯度法。
该方法基于前一迭代点的搜索方向对当前迭代点的负梯度方向进行修正来产生新的搜索方向,即搜索方向为当前迭代点的负梯度方向与前一搜索方向的线性组合。
本期大纲
1 共轭方向 在介绍共轭梯度法之间,小编首先介绍一个重要的定义—— 共轭方向 ,并给出共轭方向的一些性质。1. 共轭方向
2. 共轭方向法
3. 正定二次函数的共轭梯度法
4. 一般函数的共轭梯度法
5. 算法实现
6. 总结
定义(共轭方向):设Q是一个n×n的对称正定矩阵,若n维向量空间中的非零向量 满足
满足
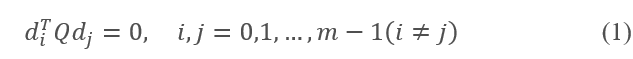
则称 是Q的共轭向量或称向量
是Q的共轭向量或称向量 是关于Q共轭的(简称共轭),也称
是关于Q共轭的(简称共轭),也称 是Q的m个共轭方向。
是Q的m个共轭方向。
例如:
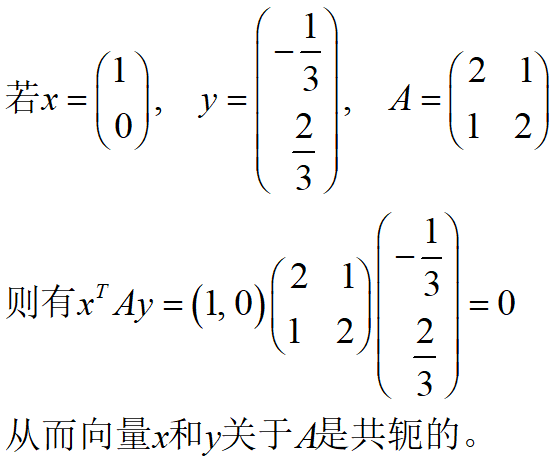
注:当 Q=I(单位矩阵)时,公式(1)变为
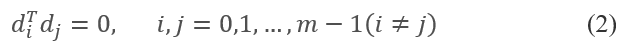
即向量  互相正交。由此可见,正交是共轭的一种特殊情况,共轭是正交的推广。
互相正交。由此可见,正交是共轭的一种特殊情况,共轭是正交的推广。
性质(线性无关性):设Q是一个n×n的对称正定矩阵,若 是Q的m个非零共轭向量,则这m个向量是线性无关的。
是Q的m个非零共轭向量,则这m个向量是线性无关的。

注:在n维的向量空间中,非零的共轭向量个数不超过n
2 共轭方向法 共轭方向 法的算法步骤如下:
在考虑普通函数之前,首先考虑如下的正定二次函数
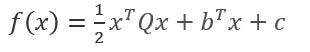
定理1:设有二次函数
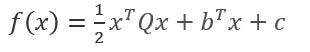
其中Q是一个n×n的对称正定矩阵,若 是Q的m个非零共轭向量,从任意一点出发
是Q的m个非零共轭向量,从任意一点出发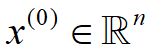 出发,依次沿这组向量进行一维搜索
出发,依次沿这组向量进行一维搜索
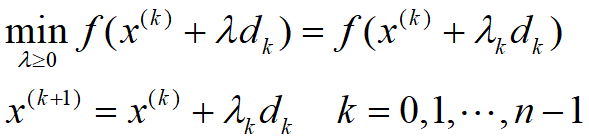
则有
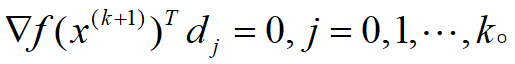
即当前点的梯度方向与之前所有搜索方向正交。
定理2(算法收敛性——二次终止性):设有二次函数
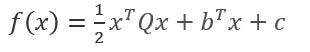
其中Q是一个n×n的对称正定矩阵,若 是Q的m个非零共轭向量,从任意一点出发
是Q的m个非零共轭向量,从任意一点出发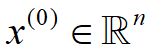 出发,依次沿这组向量进行一维搜索
出发,依次沿这组向量进行一维搜索
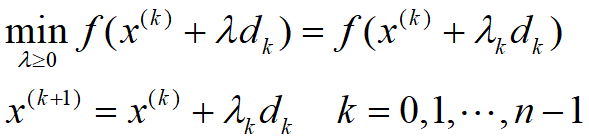
则至多经过n步算法收敛,即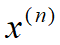 是f(x)在
是f(x)在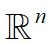 上的极小值点。
上的极小值点。
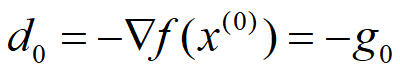
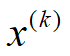 的搜索方向
的搜索方向
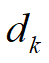 由该点的负梯度
由该点的负梯度
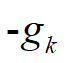 与已得的共轭向量
与已得的共轭向量
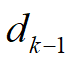 的线性组合来确定。
的线性组合来确定。
命题1:设有二次函数
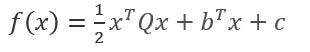
其中Q是一个n×n的对称正定矩阵。若选取初始点为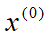 ,取
,取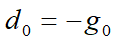 。依次从
。依次从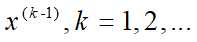 出发,沿
出发,沿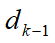 在最优步长规则下做一维线搜索,可得:
在最优步长规则下做一维线搜索,可得:
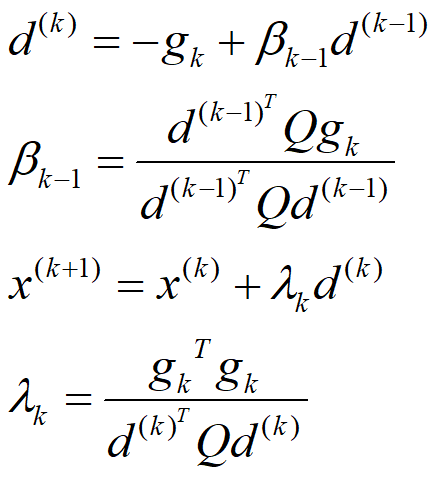
共轭梯度法的算法步骤如下:
Step 0. 选取初始点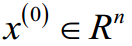 ,允许误差ε> 0,令 k=1;
,允许误差ε> 0,令 k=1;
Step 1. 计算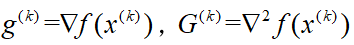 。若
。若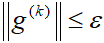 ,算法停止;.否则,转 Step 2;
,算法停止;.否则,转 Step 2;
Step 2. 依次计算
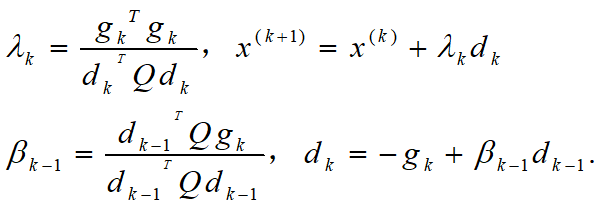
并置k=k+1,转 step 1.
定理3:对于正定二次函数,最优步长规则下的共轭梯度法经过m≤n次一维搜索后终止,且对任意的1≤i≤m,下列关系式成立:
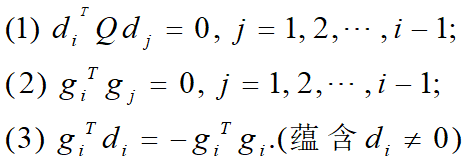
命题2:
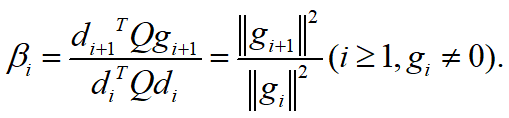
上面所讲的迭代公式要想适用于非二次函数,存在以下问题:
(1) 步长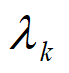 不能再用公式
不能再用公式
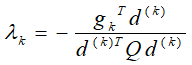 计算,必须使用其他的一维搜索方法来确定;
(2) 凡用到矩阵Q之处,需要用现行点处的Hessian矩阵
计算,必须使用其他的一维搜索方法来确定;
(2) 凡用到矩阵Q之处,需要用现行点处的Hessian矩阵
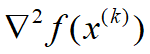 代替;
(3) 有限步内迭代达不到极小点。
代替;
(3) 有限步内迭代达不到极小点。
迭代的延续:
(1) 直接搜索:即总用公式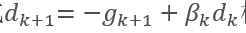 构造搜索方向。
构造搜索方向。
一般函数的FR共轭梯度法的算法步骤如下:
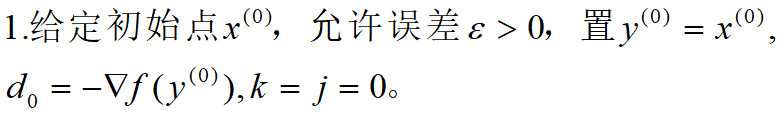
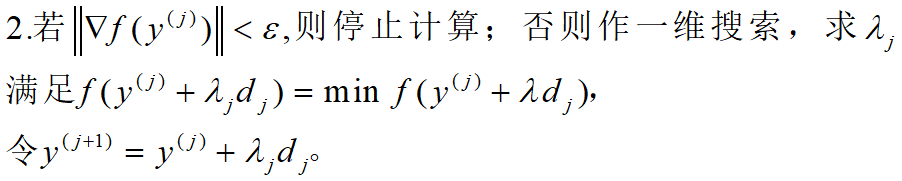

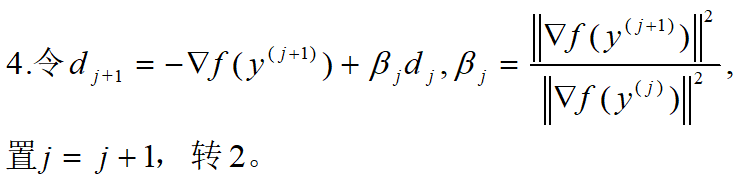
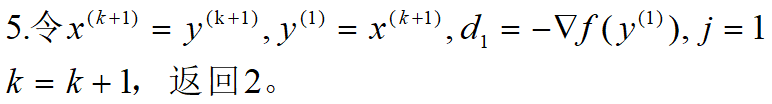
例1:求解无约束优化问题
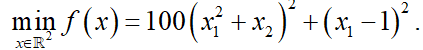
该问题有精确解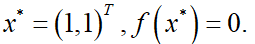
解:调用格式如下:
function [X,Y,Error] = frcg(x0)
%使用FR共轭梯度法求解无约束问题:min f(x)
%使用非精确Armijo搜索步长规则
%输入:x0为初始点,fun为目标函数,grad为梯度函数
%输出:X,Y分别为每一步的迭代点及相应函数值,Error为误差
tic
%% 初始化参数
f = @(x)100*(x(1)^2-x(2))^2+(x(1)-1)^2; %目标函数
g = @(x)[400*x(1)*(x(1)^2-x(2))+2*(x(1)-1);-200*(x(1)^2-x(2))]; %一阶导数
G = @(x)[1200*x(1)^2-400*x(2)+2, -400*x(1);-400*x(1), 200 ]; %二阶导数
%% 初始化算法参数
k = 1;
n = length(x0);
e = norm(g(x0));
X = x0;
Y = f(x0);
Error = e;
rho=0.6;sigma=0.4;
%% 设定终止条件
N = 5000; %最大迭代步
E = 1e-6; %给定误差
%% 迭代
while k < N && e > E
% 计算搜索方向
if(k == 1)
d = -g(x0);
else
beta = (g(x0)'*g(x0))/(g0'*g0);
d = -g(x0) + beta*d0;
if(g(x0)'*d>=0)
d = -g(x0);
end
end
%使用Armijo法求步长
m=0; mk=0;
while(m<20)
if(f(x0+rho^m*d)
mk=m; break;
end
m=m+1;
end
g0 = g(x0);
d0 = d;
x0 = x0+rho^mk*d; %迭代公式
k = k+1;
X(:,k) = x0;
Y(k) = f(x0);
e = norm(g(x0));
Error(k) = e;
end
toc
end
调用格式如下:
x0 = [0;0]; %迭代初始点(可以根据需要修改)
[X,Y,E]=frcg(x0);
本问题求解结果如下:
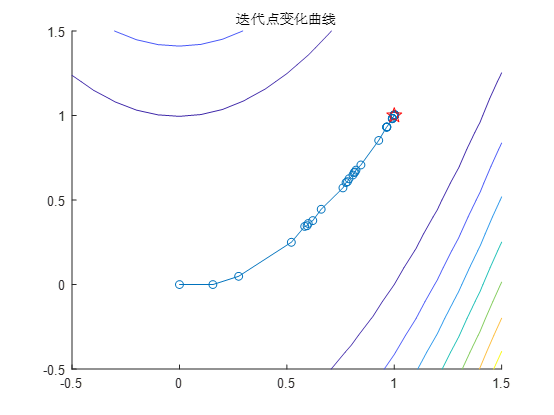
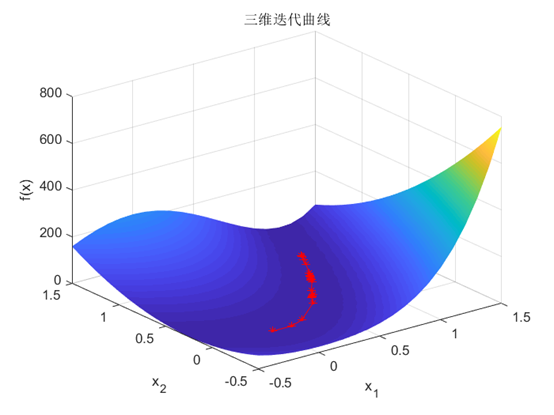
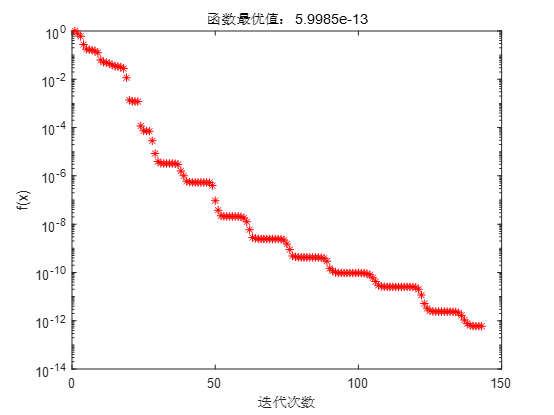
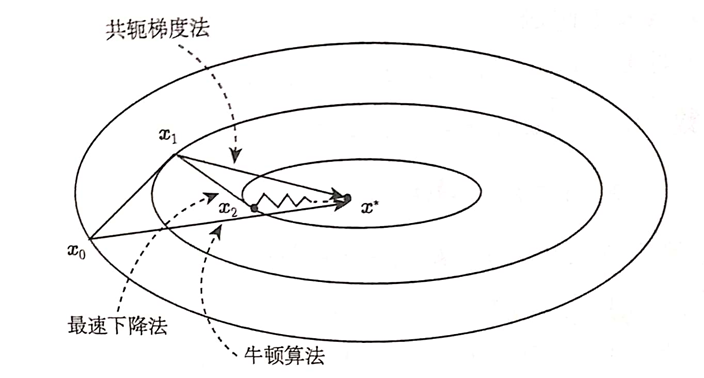 几种下降算法的迭代过程
几种下降算法的迭代过程
往期回顾
算法丨优化算法之牛顿法
算法丨优化算法之最速下降法
算法丨经典优化算法大合集(比赛备用,值得收藏)
算法丨优化算法系列之遗传算法原理
算法丨优化算法系列之遗传算法MATLAB程序设计及应用实例
算法丨优化算法系列之模拟退火算法(1)
算法丨优化算法系列之模拟退火算法(2)——0-1背包问题
参考文献:马昌凤.最优化方法及其 Matlab 程序设计[M]. 科学出版社, 2010.























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








