算法分析及分析实例

He calculated just as men breathe, as eagles sustain themselves in the air.
                                                                             - Francois Arago
对算法估计的熟练程度要如同人们称赞大数学家欧拉一样，计算如同呼吸。

 

算法分析的主要任务为 算法正确性分析 和 算法复杂度分析。而我们主要讨论算法复杂度分析方法。

一.大O记号

在分析算法之前我们要了解大O记号的作用。大O记号是算法复杂度分析的利器。

对一个特定算法，我们可以用T(n)来表示算法处理数据规模为n时所消耗的时间(n>>2)(如图1-1,横轴n表示输入规模，纵轴f(n)表示消耗时间。）

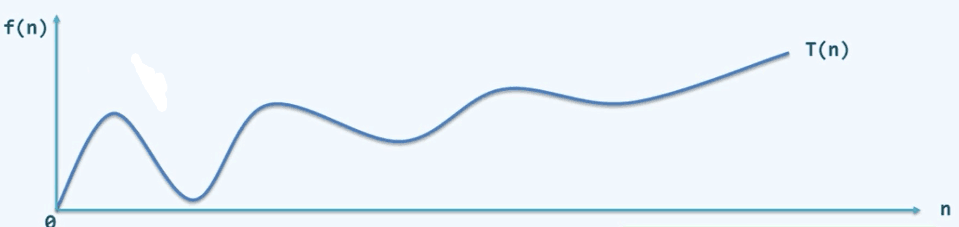
　　　　　　　　　　　　　　　　　　(图1-1)

而大O就是T(n)的上届渐进。T(n) = O(f(n))且有 c>0,当n >> 2 后，有T(n) < c * f(n) .　　如下图T(n)到O(f(n))：

O(f(n))和T(n)的比较可以通过图1-2看出：

　　　　　　　　　　　　　　　　　　(图1-2)

与T(n)相比，虽然不那么精确但是O(f(n))更加简洁，更能反映时间的增长趋势。

与大O记号性质类似，还有反映T(n)趋势的两种记号分别是Θ(f(n))和Ω(f(n)),他们则分别是T(n)的平均渐近和下届渐近。如图1-3:

 

　　　　　　　　　　　　　　　　　　　(图1-3)

 

既然我们已经掌握了大O记号的使用，那我们可以来总结一下大O表示的常见复杂度。

O(1)　　常数复杂度(含RAM模型基本操作)

O(n)　　线性复杂度

O(n^c)　　多项式复杂度包括O(n)

O(2^n)　　指数复杂度(被认为难解的，随n增长极快)

从O(n^c)到O(2^n)，是从有效算法到无效算法的分水岭。note:很多问题的O(2^n)算法容易设计出，但是O(n^c)的算法却很难设计出，甚至肯无法设计出。

各种复杂度比较：如图1-4

 

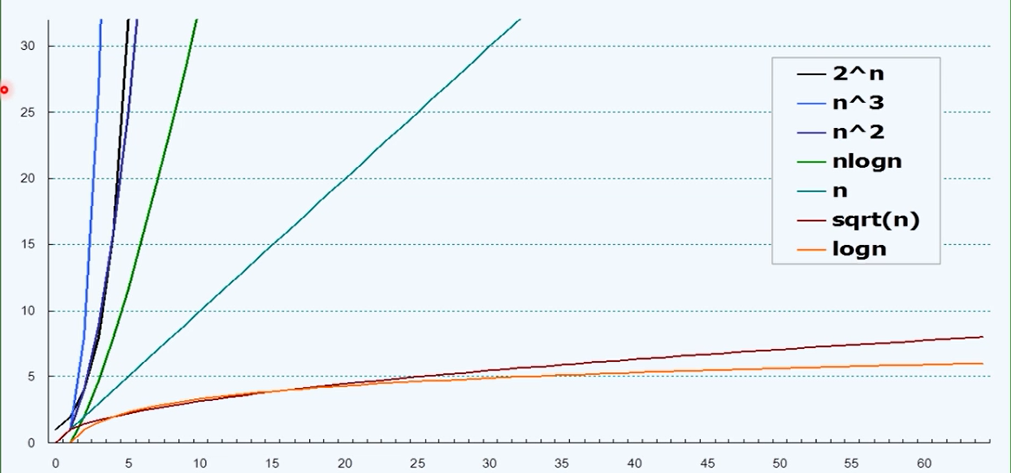
　　　　　　　　　　　　　　　　(图1-4)

 

二.算法分析

为分析某一特定算法，再掌握了大O记号这个复杂度分析工具的使用后，我们需要了解复杂度分析的方法：

复杂度分析的主要方法：

• 迭代：级数求和
• 递归：递归跟踪 + 递推方程
• 猜测 + 验证

 几类级数用于算法中迭代的复杂度分析：

算数级数(与末项平方同阶)：T(n) = 1+2+3........+n = n(n+1)/2 = O(n^2)

幂方级数(比幂次高出一阶)：T(n) = 1^2 + 2^2 +.......+n^2 = n(n+1)(2n+1)/6 = O(n^3)

几何级数(a > 1)：与末项同阶 T(n) = a^0 + a^2 + .......+a^n = (a^n+1  - 1)/(a - 1) = O(a^n)

收敛级数：1/1/2 + 1/2/3 + 1//4 + .......... + 1/(n-1)/n = 1 - 1/n = O(1)

 调和级数：h(n) = 1 + 1/2+1/3+..........+1/n = O(logn)

 对数级数：log1+log2+log3+...........+logn = log(n!) = O(nlogn)

 举栗子利用算数级数分析循环(迭代)复杂度：

栗子1：

for(int i=0; i < n; i++)
for(int j=0; j < n; j++)
    ................//其他操作

算数级数：n+n+n+.......+n = n * n = O(n^2).得出此循环复杂度为O(n^2).

 栗子2：

for(int i=1; i < n; i << 1)
for(int j=0; j < i; j++)
            ..........其他操作

几何级数：1+2+4+.........+2^|_log2(n-1)_| = 2^[log2n] - 1 = O(n)

三.实例分析：

插入排序 复杂度分析：

#include <iostream>
using namespace std;
#include <vector>
class project{
    public:
        void xzpx(){
            for(int i=1; i<a.size(); i++){
                key = a[i];
                int j=i-1;
                while(j>=0 && a[j]< key){
                    a[j+1] = a[j];
                    j--;
                }
                a[j+1] = key;
            }
            
        }
        project(){}
        
        int key;
        vector<int> a={5,2,4,6,1,3};
};

int main()
{
    project p;
    p.xzpx();
    for(auto i:p.a){
        cout << i << endl;
    }
    return 0;
}

算数级数，一眼飘过去复杂度是O(n^2)

归并排序复杂度分析：

#include <stdio.h>
using namespace std;

void merge( int a[] , int left , int middle , int right ){
    int l_len = middle - left;
    int r_len = right - middle - 1;
    int l_a[l_len];
    int r_a[r_len];
    int i,j,k=left;
    for( i = 0 ; i <= l_len; i++ )
        l_a[i] = a[i+left];
        
    for( j = 0 ; j <= r_len ; j++)
        r_a[j] = a[j+middle+1];
      
    i = 0;j = 0;
    while( i <= l_len && j <= r_len )
    {
        if( l_a[i] < r_a[j] )
            a[k++] = l_a[i++];
        else
            a[k++] = r_a[j++];
    }
    while( i <= l_len )
        a[k++] = l_a[i++];
    while( j <= r_len )
        a[k++] = r_a[j++];
}

void merge_sort( int a[] , int left , int right ){
    int middle;
    if( left < right )
    {
        middle = ( left + right ) / 2;
        merge_sort( a , left , middle );
        merge_sort( a , middle+1 , right );
        merge( a , left , middle , right );
    }
}

int main(){
    int a[]={5,4,3,2,1};
    merge_sort(a,0,4);
    for(int i=0; i<5; i++){
        printf("%d\n",a[i]);
    }
    return 0;
}

归并排序递推式： T(n) = c (n=1) || 2T(n/2) + cn (n>1)

递推式无法求解，需要结合递推跟踪分析：

可以分析出只有合并的时候才费时间，并且每层所有合并共消耗cn，而一共log2n+1层。所以耗时cn(log2n+1),即O(n*logn),相比插入排序的O(n^2)复杂度要好。 

 

感觉迭代的算法分析交常见吧。也容易分析些。

 

图片来源：学堂在线《数据结构(上)》

转载于:https://www.cnblogs.com/HonkerYblogs/p/10581264.html