n条直线相交最多有几个邻补角_【培优系列】[七下] 相交线与平行线（1）——对顶角与邻补角（1）...

一、前导知识

1、对顶角和邻补角的定义

2、握手模型(点击可查看)

二、例题呈现

【例】下面各图中的下面各图中的直线都相交于一点

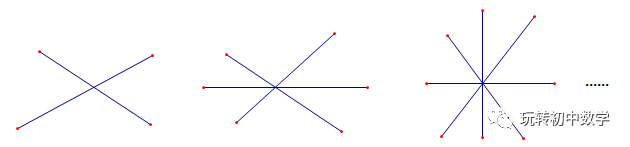
(1)请观察图形并填写下表：

(2)若n(n为大于1的整数)条直线相交于一点，则共有多少对对顶角？

共有多少对邻补角？

【分析】

方法1：数数，找规律

2条直线相交于一点会形成2对(即2×1)对顶角，4对(即2×2×1)邻补角

3条直线相交于一点会形成6对(即3×2)对顶角，12对(即2×3×2)邻补角

4条直线相交于一点会形成12对(即4×3)对顶角，24对(即2×4×3)邻补角

...

n条直线相交于一点会形成n(n-1)对对顶角，2n(n-1)对邻补角

方法2：对顶角和邻补角的定义+"握手模型"

(1)对顶角：有一个公共顶点，并且两边互为反向延长线的两个角，互为对顶角

(2)邻补角：有一条公共边(也有一个公共顶点)，且另一边互为反向延长线的两个角，互为邻补角

从定义中我们发现：无论是一对对顶角，还是一对邻补角，它们都有1个公共顶点，那么当两条直线相交时，1个交点就决定了2对对顶角和4对邻补角，我们只需要知道n条直线相交最多形成几个交点就可以了，(当然这道题中n条直线相交于一点，我们要把其看作若干个交点重合了)

三、类题练习

1、两条直线相交只有______个交点；三条直线两两相交，最多有______个交点；n条直线两两相交，最多有______个交点。

2、n条直线两两相交，会形成________对对顶角，________对邻补角。

------------------------------------------------------------

【参考答案】

1、1；3；n(n-1)/2

2、n(n-1)；2n(n-1)(分析方法与例题类似，也就是说无论是否相交于一点结论是一样的)

------------------------------------------------------------

欢迎关注Leo老师的微信公众号

欢迎加入Leo老师发起的公益辅导QQ群(群号：192551958)

跟众多"大牛"老师/学霸一起开启精彩的学习之旅吧！