作为一个应用者来说,要了解一个模型的顺序是:1)为什么要用这个模型解决问题?2)这个模型是什么,可以解决什么问题?3)模型怎么用?4)应用领域是什么?解决了哪些问题?5)模型的归档与应用划分?
人话篇:广义线性模型到由来
从逻辑回归模型开始,我们连续讲了好多集有些相似又特点各异的几种统计模型。它们有个统一的旗号,叫做「广义线性模型」(generalized linear model)。 许多在大学里学过一点统计的读者,可能对广义线性模型还是会感到比较陌生。为什么这些模型能被归为一个大类?它们的共同点在哪里?今天我们就和大家一块用说人话的方式再来系统地认识一下,广义线性模型到底是何方神圣。
在耐着性子把这篇文章读完之前,大家肯定会想,为什么要学习广义线性模型呢?毕竟光是理解线性模型的各种用法就已经够头疼的了,再加个广义更绕不清楚了。
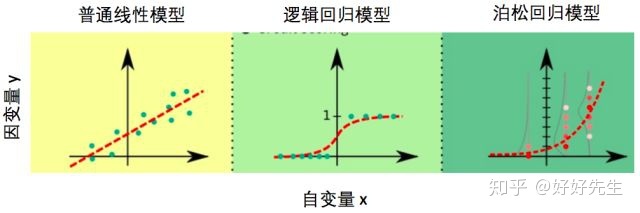
普通线性模型对数据有着诸多限制,真实数据并不总能满足。而广义线性模型正是克服了很多普通线性模型的限制。在笔者的心里,广义模型能解决的问题种类比普通线性模型多很多,用图来表示,大概就是这样的:
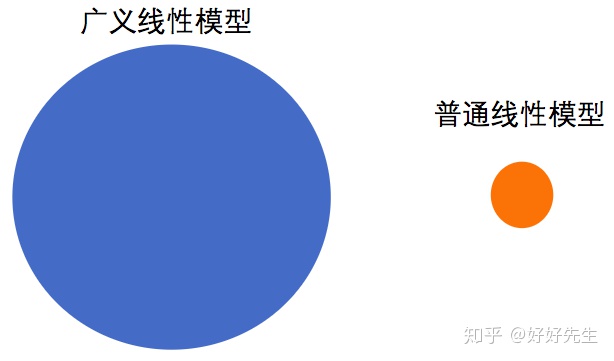
我们将要回到广义线性模型的本质,从广义线性模型的
三个要素——
- 线性预测
- 随机性
- 联系函数
入手,在理论层面系统深入地了解广义线性模型。
- 线性预测
- 各路线性模型的共同点:线性预测
不管是普通线性模型,还是广义线性模型,既然打着「线性模型」旗号,总该是有个原因的吧?这里的「线性」指的是多个自变量的「线性组合」对模型预测产生贡献,也叫做线性预测,它具有类似于下面的形式:
首先这个类似与我们线性代数里的线性系统,看看我的总结:
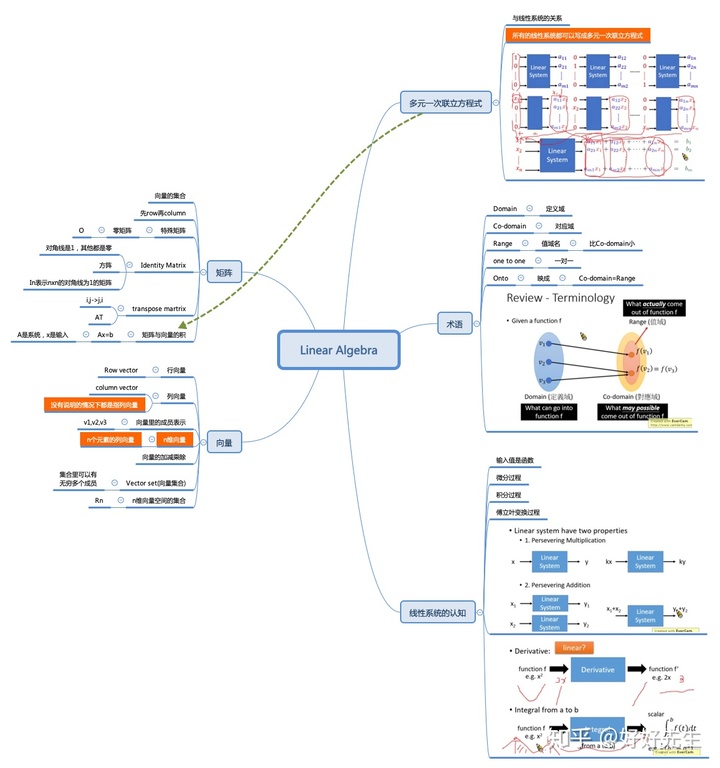

这个形式读者们已经非常熟悉了,因为之前讲的所有模型使用的都是线性预测。
统计模型中的β0、β1、β2等是模型的参数,如果把模型看成是一个音箱,这些参数就像看是音箱上一个个控制声音的旋钮。为啥音箱得要怎么多旋钮呢?因为虽然拧每一个旋钮达到的效果不同,可能β0管的是低音炮部分,β1管的是中音区,β2管的是高音区,模型里面需要这么多参数也是为了控制各种自变量对因变量的影响的。
- 为什么各种常用的模型都选择线性预测呢?
当我们调节某一个旋钮的时候,我们当然希望声音的效果与旋钮拧了多少成正比,如果拧了一圈声音跟蚊子叫一样,而拧了两圈声音突然震耳欲聋,这样的音箱用起来就得经过反反复复地调节才能找到最佳音量,非常的不方便。统计模型的在寻找最优参数的时候做得就是调节音量这件事,使用线性预测使得β0、β1、β2这些参数改变的值与预测的结果的改变值成正比,这样才能有效地找到最佳参数。
2. 随机性— 统计模型的灵魂
- 我们之所以会建立统计模型,是想研究自变量(模型的输入)与因变量(模型的输出)之间的定量关系。
通过模型计算出来的自变量的预测值与因变量的测量值越接近,就说明模型越准确。
虽然在建立模型时,我们希望统计模型能准确地抓住自变量与因变量之间的关系,但是当因变量能够100%被自变量决定时,这时候反而没有统计模型什么事了。
典型的例子是中学时学习的物理定律,我们都知道,物体的加速度与它受的合力大小成正比,也就是说给定物体的质量和受力大小,加速度是一个固定的值,如果你答题的时候写,「有一定的概率是a,也有一定的概率是b」,物理老师肯定会气得晕过去。
统计模型的威力就在于帮助我们从混合着噪音的数据中找出规律。假设这个世界还没有人知道物体受的合力大小与加速度成正比,为了验证这一假说, 你仔细测了小滑块 在不同受力条件下的加速度,但由于手抖眼花尺子烂等等理由,哪怕是同样的受力,多次测量得到的加速度也会不一样,具有一定的随机性。
也就是说,由于测量误差的存在,测量到的加速度(因变量y)与物体的受力大小(自变量x)之间不是严格的正比关系。
- 统计模型是怎样从具有随机性的数据中找到自变量和因变量之间的关系的呢?
原因在于是测量随机误差也是有规律的。在测量不存在系统性的偏差的情况下,测量到的加速度会以理论值为平均值呈正态分布。抓住这一统计规律,统计模型就能帮我们可以透过随机性看到自变量与因变量之间的本质联系,找出加速度与受力大小的关系。
如果不对自变量的随机性加以限制,再好的统计模型也无可奈何。试想一下,假如测量到的加速度值是不认真做实验的某个同学随手编的数值,那就不能保证它的平均值与实际值接近,自然也就无法正确地计算出加速度与受力大小的关系。
虽然在加速度的例子里面,因变量y的随机性来源于测量误差,但是实际应用中,y的随机性远不止测量误差,也有可能是影响y值变化的一些变量没有包含在模型中。比如一个公司的薪水由工龄,工作岗位和每月工时三个因素决定,但是在用模型预测薪水的时候,只用了工龄和工作岗位两个因素,这时模型就会把由工时不同导致的薪水不同看做是随机误差。
- 统计模型并不在意y的随机性是由什么产生的:统计模型把因变量y中不能被模型解释的变化都算在误差项里面,并且通过对误差作出合理的假设,帮助我们找到自变量与因变量之间内在的关系。
如何对随机性作出合理的假设,得根据具体情况具体分析,这也就演化出了各种各样的统计模型。
- 各路统计模型如何对付「随机性」?
在统计模型中,当自变量取特定值(测量数据也称观测数据),因变量y的随机性由y的概率分布来决定。
无论是普通线性模型还是广义线性模型,预测的都是自变量x取特定值时因变量y的平均值。
因变量y的实际取值与其平均值之差被称为误差项,而误差的分布很大程度上决定了使用什么模型。
我们下面就来回顾一下在不同的模型里面
- 误差项得满足什么样的分布?
1)普通线性模型的基本假设之一是误差符合方差固定的正态分布(高斯分布)。只有一个因变量的普通线性模型具有下面的形式:

模型的输出β0+β1*x预测的是y的平均值,而误差项ε描述了y的随机性。
普通线性模型中的方差不随自变量x取值的变化而变化。
在线性回归模型里面,系数 β0,β1 决定了回归线的走向,也就是 y 与 x 之间的定量关系,代表误差项大小的 σ 代表了模型有多准确。通常情况下,线性回归模型假设误差项 ε 服从平均值为 0,方差为 σ2 的正态分布,而且方差的大小不随着预测变量 x 值改变,也叫做同方差性(Homoscedasticity)。换句话说,同方差性就是指误差项的方差是一个常数,与实验条件无关。
在通过父母平均身高预测子女身高的例子里面,同方差性意味着无论父母平均身高是两米还是一米六,线性模型预测的子女身高和真实身高之间的绝对差距是近似的。如果随着父母身高增加,子女的预测身高与真实身高的差距也有变大的趋势,同方差性就不再满足了,以后我们会讲到如何在同方差性不能满足的情况下做回归模型。
当误差项ε不再满足正太分布,或者误差项的方差会随着x的变化而变化的时候,普通线性模型就不够用了。
由于正太分布描述的是一个连续变量的分布, 当因变量y是类别变量或是计数变量这样的非连续变量时 ,显然误差项就不能满足普通线性模型关于误差得是正态分布的要求,这时候就需要广义线性模型来救场了。
根据定义,正态分布的数据是连续的,对称的,并在整个数字线上定义。这意味着任何离散,不对称或只能在有限范围内使用的数据,实际上都不应使用线性回归建模。该模型专门设计用于非正态数据。这是广义线性模型出现的地方。
2) 逻辑回归
咱们先从最常用的逻辑回归模型说起。逻辑回归模型预测的是因变量y=1的概率P(y=1),它具有下面的形式:

对逻辑回归记不太清或者不熟悉的读者可以先不用纠结等式左边复杂的形式,我们一会儿再说。 与普通线性回归不同,逻辑回归的模型形式似乎并不能直接体现出y的误差项,毕竟等式的右边没有一个。
- 那么y的随机性是如何在逻辑回归中体现出来的?
在知道P(y=1)的情况下,y有可能取0也有可能取1,这是y随机性的来源。
有趣的是,当我们用概率分布来描述y的随机性时,我们会发现,这不就是P(y=1)吗?由于y只能取两个值,知道取1的概率,自然就确定了y的概率分布,也就是说,y的随机性恰好被y的平均值刻画了,这与普通线性回归完全不一样。在普通线性回归里面,我们强调了,当y的预测值改变时,y实际值的方差是不变的,而在逻辑回归模型里面,模型的预测值同时也决定了方差。
3) 泊松回归
下面再看看针对因变量是整数变量情形的泊松回归,泊松回归具有下面的形式
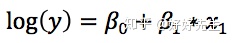
- 那泊松回归是如何处理y的随机性的呢?
泊松回归模型认为给定自变量的取值,因变量y满足泊松分布,模型的输出e^(β0+β1*x1)预测的是y的平均值,由于泊松分布只有一个参数,知道了分布的平均值整个分布也就确定了.
于是泊松分布中y的误差的分布也就由y的平均值决定了,这一点倒是和逻辑回归模型异曲同工。
4) 总结
对比普通线性模型,逻辑回归模型,以及泊松回归模型,我们可以发现这几个模型除了等式左边形式不同,当因变量取特定值时,这些模型所假设的y的随机分布形式也不一样,如下图:
3. 联系函数
广义线性模型绕不开的联系函数(link function)
说完了随机性,下面再来看看广义线性模型的最后一个要素:联系函数。联系函数是啥?
它是一个关于因变量y的函数,它把前面说到的线性预测的结果与因变量y的值之间建立一座桥梁。
在学习统计的人看来,它就是广义线性模型中那个最匪夷所思最麻烦的一项:
它是逻辑回归中的
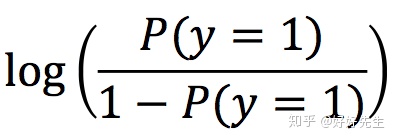
它是定序回归中的
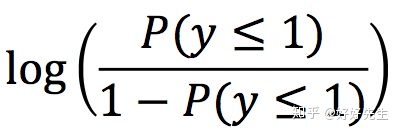
它是泊松回归中的
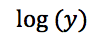
在我们最熟悉的普通线性回归中,它就是y本身,是最朴实的联系函数。从这个角度,普通线性模型也被包含在里广义线性模型的框架底下,只是使用的联系函数以及对于y的随机性假设与其它广义线性模型不同。如下图所示。

- 联系函数为什么会在各个模型中具有不同的形式?
首先,是为了把y的取值范围变换成负无穷到正无穷。
这样就与模型中等式右边的线性预测项的取值范围一致了。当然,对于任意类型的因变量y,符合上面这个条件的变换都可以有无数个,那为什么我们会取上面这些特定的形式呢?
在理论层面上,当y是二项分布时,使用逻辑函数作为联系函数,能够使得模型有一些有效的解法;当y是泊松分布的情况下,使用对数函数作为联系函数,也有同样的效果。在实际应用中,上面提到的联系函数形式也常常能有效地拟合数据,这些原因综合导致了它们是最常用的联系函数形式。

上面罗列的理由只能说明这些常见的联系函数使用起来比较方便,但并非是说它们是唯一合法的联系函数。在以后读者们在接触到更多的广义线性模型的时候,看到新的联系函数不要被吓到,虽然形式可能很复杂,但是功能不外乎是让y的取值范围与预测值范围一致,以及让模型比较好地拟合当下的数据。
一个实用的广义线性模型总结
最后,我们用一张表格来总结各种不同的线性模型。在表中,我们把普通线性模型看做是广义线性模型的一个特例。
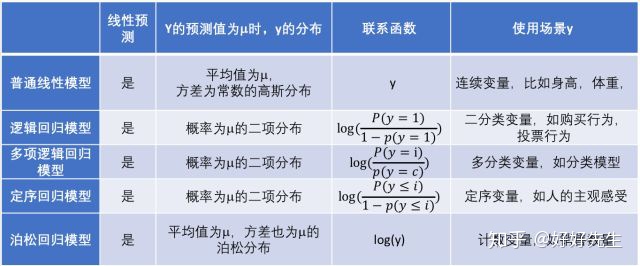

一个吃货的线性模型总结
最后,作为一个吃货,竟然觉得线性模型与火锅有一种神似,在这里和大家分享一下。总有一款线性模型适合你的数据,就像总有一种火锅能打动你。数据就像是火锅的食材,而选择哪款线性模型(回归系数beta向量)就像是选择汤底。我们都知道,汤底得按照食材的特性选择,才能释放出食材的全部美味。
对于新鲜又质量上层的肉片,清淡一点的汤底能更好得带出食材的香味,就像当因变量属于正常正态分布的数据时,选用普通线性模型就能得到良好的效果;对于本身味道比较重的食材,比如毛肚百叶等,经过麻辣的汤底的洗涤再放到嘴里简直爽到飞起,就像当因变量是二元变量或计数变量时,用逻辑回归模型或者泊松回归模型才能较好地拟合数据。
吃火锅时汤底是很关键,但蘸料(连接函数)的妙用也会锦上添花,极大地提高食物的美味程度。联系函数之于广义线性模型,就如蘸料之于火锅。蘸料一般选择基本款就可以了,就像根据因变量y的分布,联系函数的选择也有一些万能基本款,遇到特殊问题的时候,也可以灵活变通,选择使用「口味」更适合的联系函数。
鬼话篇:GLM模型
GLM允许目标变量比正态分布更灵活。链接函数将线性预测变量连接到目标变量。假定结果是由系统性因素和随机性因素共同驱动的。系统组成部分是指预测变量所解释的变化。例如,我们认为驾驶员的年龄与个人汽车保单的预计索偿频率有关。因此,驾驶员的年龄是系统组成部分的一部分。从广义上讲,我们的目标是尽我们所能使用预测变量来解释变异性。
广义线性模型(GLM)可以看作是多元线性回归模型的概括。GLM也由三个组成部分组成,它们与线性回归模型的组成部分相似,但略有不同。具体而言,GLM由以下组成:
- 输出变量Y,假定该变量的所有观测值均独立于指数族分布;
- 由k个输入变量X1,X2,…,Xk组成的向量;和
- 一个由k + 1个参数组成的向量b0,b1,...,bk 和一个链接函数g(),使我们可以将g(E(Y))编写为输入变量的线性组合。那是:
其中Y_mean = E(Y)
同样,我们的目标是确定最佳参数值和定义Y的概率分布,但是现在我们不再仅遵循正态分布就被约束为Y。
在GLM假设下,Y现在可以遵循“指数族”内的任何概率分布,不仅包括指数分布,而且还包括正态,伽马,卡方,泊松,二项式(对于固定数量的轨迹),负二项式(针对固定数量的故障),β和对数正态分布等。(normal, gamma, chi-squared, Poisson, binomial (for a fixed number of trails), negative binomial (for a fixed number of failures), beta and lognormal distributions, among others.)
链接函数的目的是转换输出变量,以便我们可以将其表达为输入变量的线性组合(不是,通常是错误地认为是这样,将输出变量转换为正态性)。
根据我们假设要绘制输出分布的概率分布,有一些常用的链接函数。
例如:

因此,在指定GLM时,必须指定输出概率分布函数和链接函数。
标准线性回归模型是GLM的一种特殊情况,其中我们假设一个正态概率分布和一个身份链接。
代码篇:应用场景
场景1:计数数据
计数数据是只能采用非负整数值的任何数据。顾名思义,它通常是在一定时间段内对特定类型事件的观察计数时出现的。例如,每年在一个十字路口的车祸数量;或每天失败的次数。
为了使GLM适合于对数据进行计数,我们需要为模型假设一个概率分布和链接函数。由于计数数据是离散的,因此概率分布也必须是离散的。
在这种情况下,最常见的选择是具有对数链接功能的泊松或负二项式分布。
为了使泊松或负二项式GLM适合我们的数据,我们可以使用Python的statsmodels包,其语法类似于以下内容:
import pandas as pd
import statsmodels.api as sm
count_model = sm.GLM(count_data['Y'], sm.add_constant(count_data[['X1', 'X2']]), family=sm.families.Poisson(sm.genmod.families.links.log)).fit()此语法假定我们的数据集采用称为count_data的pandas dataFrame的形式,其输出变量Y以及输入变量X1和X2,并且我们要适合Poisson GLM。
要拟合负二项式GLM,而不是泊松GLM,我们需要做的就是将sm.families.Poisson更改为sm.families.NegativeBinomial。
场景2:数据偏斜
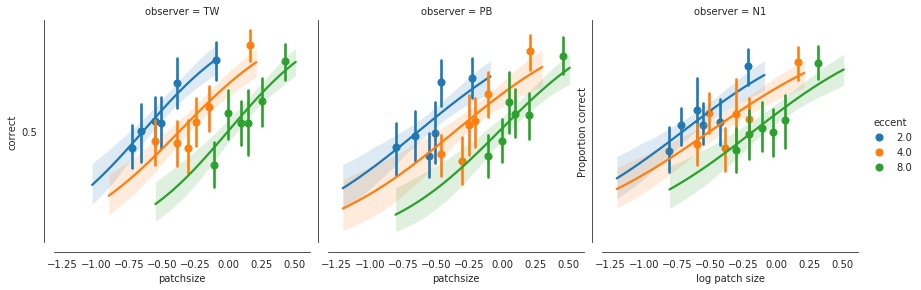
尽管非对称数据可以在两个方向上偏斜。实际上,您将遇到的大多数非对称数据都是正确或正偏的,例如下面绘制的数据集。

和以前一样,为了使GLM适应此数据,我们需要选择概率分布和链接函数。我们的概率函数需要正偏,在这种情况下,最常见的选择是带有对数链接的伽马分布。
要使用statsmodels包将gamma分布与数据的日志链接配合起来,我们可以使用与Poisson GLM相同的语法,但将sm.families.Poisson替换为sm.families.Gamma
仅针对大于0的值定义伽马分布。因此,如果我们的输出变量Y可以取负值或零,那么可能需要在拟合之前通过向输出变量添加足够大的常数来转换我们的数据该模型。
例如,如果我们的输出变量可以采用任何非负值(包括零),则可以在拟合模型之前对所有Y值加上0.01,从而将其转换为最小值,从而将其转换为0.01,从而对其进行转换。
场景3:二进制数据
与前两个示例一样,可以使用statsmodels包来拟合上述GLM,并使用与以前相同的语法,但是将sm.families.Poisson替换为sm.families.Binomial,将sm.genmod.families.links.log替换为sm.genmod.families.links.logit。
也就是说,如果我们假设我们的数据集称为binary_data,并且我们的输入和输出变量使用以下命令,则如先前定义:
binary_model = sm.GLM(binary_data['Y'], sm.add_constant(binary _data[['X1', 'X2']])
, family=sm.families.Binomial(sm.genmod.families.links.logit)).fit()另外,我们也可以使用Python scikit-learn包的sklearn.linear_model.LogisticRegression函数来拟合此模型。
实际篇: 这些模型的具体用法
元数据:

import numpy as np
import scipy as sp
import pandas as pd
import patsy # pasty功能:线性分析里因素分析(方差分析)
import seaborn as sns # 作图包
import statsmodels.formula.api as smf # statsmodels
import statsmodels.api as sm
import matplotlib.pyplot as plt
import itertools
%matplotlib inline
sns.set_style("white")
gf = pd.read_csv('gforces.txt', sep='t')
# make all columns 转换字符串中所有大写字符为小写:
gf.columns = [c.lower() for c in gf.columns]
print(gf)

- 请注意,我们尝试预测的响应变量(signs)仅采用以下两种可能的值之一:受试者显示了停电迹象(y = 1)或没有显示(y = 0)
- 顺便说一句:数值0和1习惯上是为了方便数学使用。 可以将其想象为“存在某种东西(1)而缺少某种东西(0)”。
- 如果我们对这些数据拟合普通的(高斯误差)线性回归,会发生什么?
fit_lm = smf.glm('signs ~ age', gf).fit()
print(fit_lm.summary())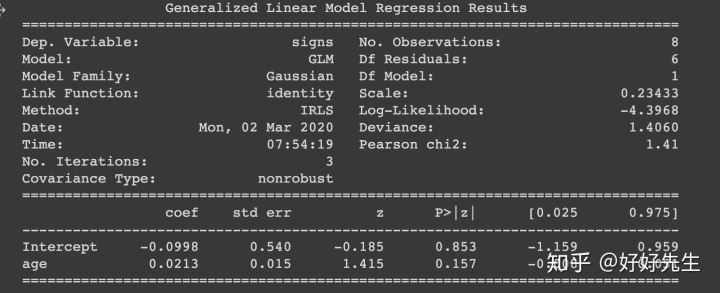
# Let's have a look at the model predictions
sns.regplot('age', 'signs', gf)
sns.despine(offset=10);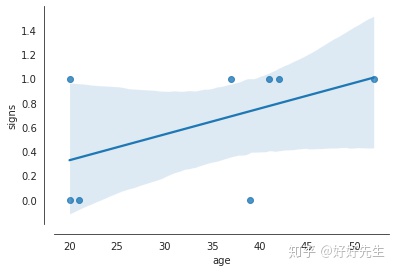
Notice how the data are only 0s or 1s, but that our model can happily predict values outside this range. Moreover, our model expects the errors to be Gaussian, and they clearly won't be. Therefore, this linear model is not appropriate for these data.
我们的线性模型应对这种二项分布的问题是不适用的
What we want instead is to change the link function () from the identity (i.e. our prediction is just with Gaussian errors) to something more appropriate for the data we have. We are going to transform the linear predictor into a more appropriate range, by changing the link function.
我们通过改变链接函数从以前的identity改成适合数据本身的链接函数
Our linear predictor can theoretically range from -inf to +inf. We want something that maps this range into the range 0--1. There are a number of options, but the most common is the logistic function:
我们的线性预测器在理论上是可以在正负无穷的,我们通过链接函数把它转到二值图,最常用的就是逻辑回归

图像如下图所示:
def logit(x):
return(1. / (1. + np.exp(-x)))
x = np.linspace(-5, 5) # imagine this is the linear predictor (inner product of X and beta)
y = logit(x)
plt.plot(x, y)
sns.despine(offset=10)
plt.vlines(0, 0, 1, linestyles='--')
plt.hlines(0.5, -5, 5, linestyles='--')
plt.yticks([0, 0.5, 1])
plt.xlabel('Linear predictor value')
plt.ylabel('Transformed value');
通过logit变换,我们可以将线性预测变量映射到有界范围内。 还要注意,当线性预测变量为零时,对数为0.5。
现在我们如何使用这个转换后的值来预测二分法反应?
二项分布(Binomial distribution)
由于响应变量是二分法的(“显示sign”或“不显示sign”),因此描述数据的合适概率分布是二项式分布。 就像正态分布在给定平均值和标准差的情况下在连续维度上返回概率密度一样,二项式分布在离散维度(“成功次数”)上给出了一定概率质量,给定了多个“试验”和概率为 成功, (请注意,因为a是概率,所以它可以具有从0到1的任何值)。
用来证明二项式分布的最常见示例是硬币翻转。 想象我们有一个公平的硬币(coin = 0.5),我们将其翻转50次试验。 我们期望多少个正面头(“成功”)? 二项式分布可以告诉我们。
先理解两个概念:
概率密度函数(pdf)和概率质量函数(pmf)
概率质量(mass)函数:各个分类的概率。
概率密度(density)函数:数据落在某一段连续的区间的概率。
然后为何一个叫做质量,一个叫做密度。主要是他们从英文翻译过来的。所以得从英文解释。
概率质量函数:
mass强调的是一个聚集在一起的物体,就是它一个块一块的。这和离散型数据很像,就是一堆数据属于某个类。他们是聚集一块一块的。所以用mass这个词来描述他们的概率。翻译成中文就变成了概率质量函数。你可以这么记忆:离散型数据是块状物体,物体是有质量,所以叫做概率质量函数。
概率密度函数(Probability Density Function)
这个是描述连续性数据。就是落在某个区间内的概率多大。这个就像液体,液体是连续的。同等体积有些液体重有些液体轻,用密度这个词描述会更合适。 它的缩写很意思,叫做PDF
离散概率分布也称为概率质量函数(probability mass function)。离散概率分布的例子有伯努利分布(Bernoulli distribution)、二项分布(binomial distribution)、泊松分布(Poisson distribution)和几何分布(geometric distribution)等。
连续概率分布也称为概率密度函数(probability density function),它们是具有连续取值(例如一条实线上的值)的函数。正态分布(normal distribution)、指数分布(exponential distribution)和β分布(beta distribution)等都属于连续概率分布。
# code hacked from here: http://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.stats.binom.html
n, p = 50, 0.5
fig, ax = plt.subplots(1, 1)
#ppf:累积分布函数的反函数。q=0.001时,ppf就是p(X<x)=0.001时的x值
x = np.arange(sp.stats.distributions.binom.ppf(0.001, n, p),
sp.stats.distributions.binom.ppf(0.999, n, p))
# 二项分布的概率质量函数
ax.plot(x, sp.stats.distributions.binom.pmf(x, n, p), 'bo', ms=8, label='binom pmf')
ax.vlines(x, 0, sp.stats.distributions.binom.pmf(x, n, p), colors='b', lw=5, alpha=0.5)
sns.despine(offset=10);
plt.xlabel('Number of successes')
plt.xlim(0, 50)
plt.ylabel('Probability mass');
现在想象一下,我们有一个骗人的硬币,它有90%的时间出现头。 我们现在的期望多少?
n, p = 50, 0.9
fig, ax = plt.subplots(1, 1)
x = np.arange(sp.stats.distributions.binom.ppf(0.001, n, p),
sp.stats.distributions.binom.ppf(0.999, n, p))
ax.plot(x, sp.stats.distributions.binom.pmf(x, n, p), 'bo', ms=8, label='binom pmf')
ax.vlines(x, 0, sp.stats.distributions.binom.pmf(x, n, p), colors='b', lw=5, alpha=0.5)
sns.despine(offset=10);
plt.xlabel('Number of successes')
plt.xlim(0, 50)
plt.ylabel('Probability mass');
因此,您可以看到,更改 会改变我们从给定数量的试验中期望的成功次数(等效于任何一项试验成功的机会)。
现在,通过假设我们的响应分布是二项式分布,我们可以估计显示sign随年龄变化的预期概率。 为此,我们使用对数变换后的线性预测变量作为对二项式分布中的估计。
假设数据来自二项分布,我们可以使用statsmodel的glm函数来找到使权重最大化的回归权重:
fit = smf.glm('signs ~ age',
data=gf,
family=sm.families.Binomial(link=sm.families.links.logit)).fit()
# note we don't have to specify the logit link above, since it's the default for the binomial distribution.
print(fit.summary())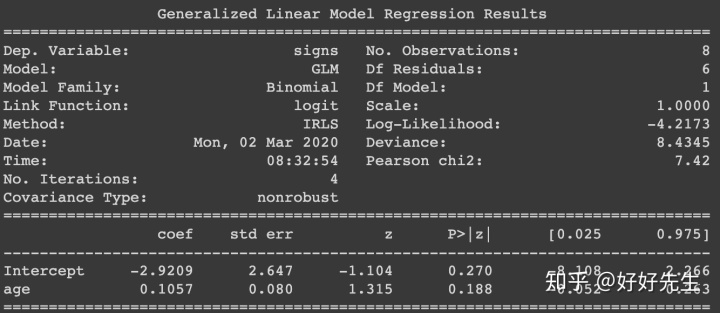
我们得到了一个具有回归系数的汇总表。 请注意,有些事情已经改变:特别是,现在看到模型族为“ Binomial”,而链接函数为logit。 这也称为逻辑回归,因为它使用了logit链接功能。
- 上面的回归系数与我们之前拟合的线性高斯模型相比如何?
print(fit.summary())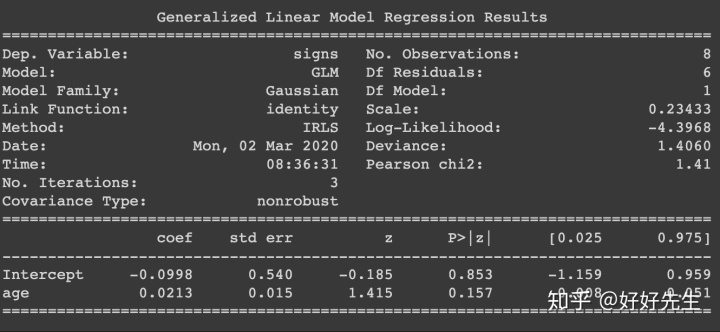
Let's run through what the regression coefficients mean in the logistic regression (fit).
(回归系数的意义):
The Intercept(截距) is the value of the linear predictor (note: not the response!) when age = 0. In this case, we can't observe an age of zero, so the intercept is not very meaningful
Aside: To make the intercept more interpretable, we could centre the age variable by subtracting its mean -- this would make the intercept equal the linear predictor value when age is at its mean in the data. We could do this within the Patsy formula by writing signs ~ center(age). We will avoid doing this here for simplicity.
# 把年龄去平均,截距才有意义
The age coefficient tells us the change in the linear predictor for an increase in age of one year.
年龄系数告诉我们随着年龄增长线性预测的变化
To work out what these mean for the response value, we need to pass them through the logit function. As an example, let's consider the prediction for the chance a 28 year old person would show blackout signs.
要弄清楚这些对响应值的含义,我们需要将它们通过logit函数传递。
- 我们考虑一个28岁的老人出现sign=1的预测
age = 28
linear_predictor = fit.params[0] + fit.params[1]*age
linear_predictor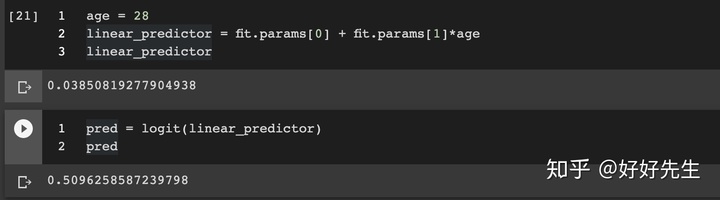
因此,对于28岁的孩子,我们的预测是他们会有51%的机会被sign。 我们也可以使用拟合对象的预测方法进行计算。 让我们为65岁的孩子做这个:
fit.predict(exog={'age':65})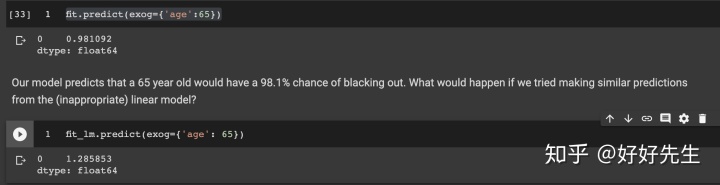
Plotting model predictions
# define expand grid function:
def expand_grid(data_dict):
""" A port of R's expand.grid function for use with Pandas dataframes.
from http://pandas.pydata.org/pandas-docs/stable/cookbook.html?highlight=expand%20grid
"""
rows = itertools.product(*data_dict.values())
return pd.DataFrame.from_records(rows, columns=data_dict.keys())
# build a new matrix with expand grid:
preds = expand_grid({'age': np.linspace(10, 80, num=100)}) # put a line of ages in, to plot a smooth curve.
preds['yhat'] = fit.predict(preds)
# add to data:
merged = gf.append(preds)
merged.tail()
g = sns.FacetGrid(merged, size=4)
g.map(plt.plot, 'age', 'yhat') # plot model predictions
g.map(plt.scatter, 'age', 'signs')
sns.despine(offset=10);
plt.ylim([-.1, 1.1])
plt.yticks([0, 0.5, 1]);
通过假设变量根据二项式分布进行分布,可以将GLM用于建模二分法响应变量。 在神经科学和心理学中经常发现二分法的响应变量:每当我们谈论“正确百分比”或类似变量时(例如上面的心理物理数据集)。
为此,我们通过logit函数“压缩”线性预测变量,使其边界介于0到1之间。该压缩过程和二项式族是更改身份链接函数和误差模型的一个示例。 这就是使GLM“泛化”的原因。
请注意,关于如何构造或解释模型的设计矩阵,没有任何改变:我们所学到的关于设计矩阵的所有内容仍然适用。
更多代码下载:
https://github.com/zjgulai/glm-introgithub.com 广义线性模型(GLM)从人话到鬼话连篇mp.weixin.qq.com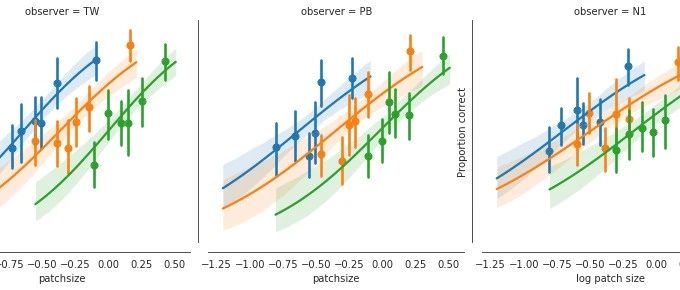








 本文以通俗易懂的语言介绍了广义线性模型(GLM)的起源、要素和应用场景。GLM是统计学中用于处理各种类型数据的模型,包括线性预测、随机性和联系函数三个核心概念。它克服了普通线性模型的局限,适用于连续、二元、计数等多种数据类型。文章通过实例展示了GLM如何在计数数据、偏斜数据和二元数据中发挥作用,帮助读者理解并掌握GLM的实际运用。
本文以通俗易懂的语言介绍了广义线性模型(GLM)的起源、要素和应用场景。GLM是统计学中用于处理各种类型数据的模型,包括线性预测、随机性和联系函数三个核心概念。它克服了普通线性模型的局限,适用于连续、二元、计数等多种数据类型。文章通过实例展示了GLM如何在计数数据、偏斜数据和二元数据中发挥作用,帮助读者理解并掌握GLM的实际运用。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








