求抛物线和直线交点_解读【每日一题70】已知抛物线与线段的交点情况，求参数（范围）...

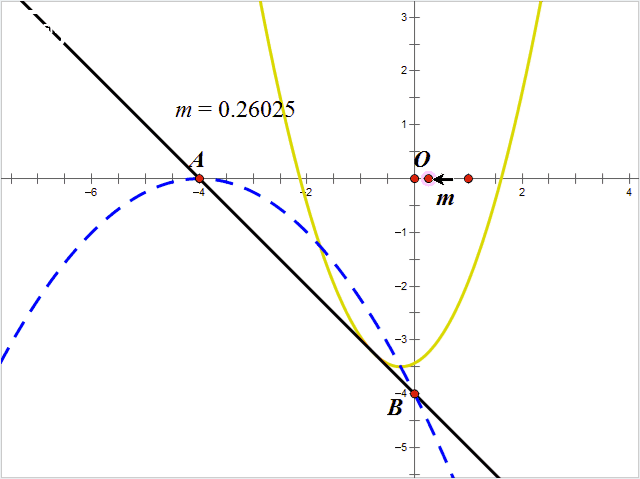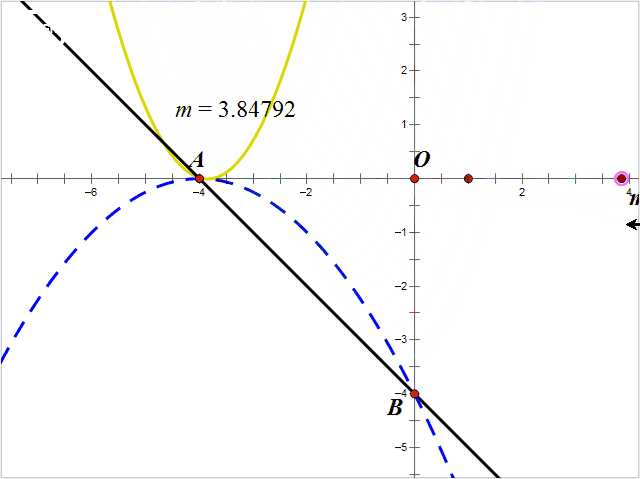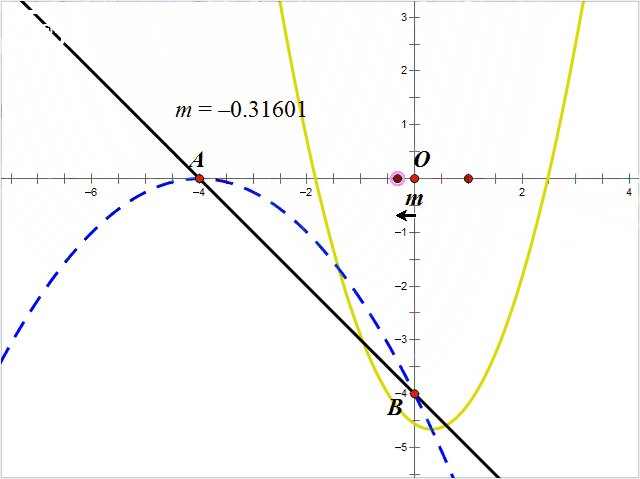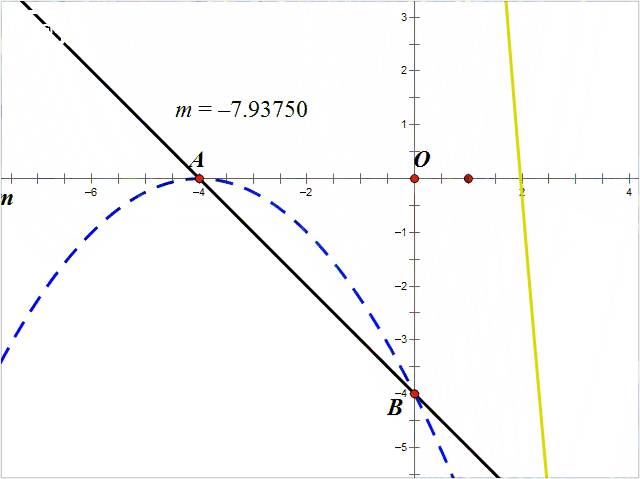
70.已知抛物线y1=－1/4(x＋4)^2顶点为A，与y轴的相交于点B，抛物线y2=x^2＋2mx＋n的顶点P在抛物线y1上，与x轴相交于C，D两点，且xC＜xD，与y轴相交于点E.

(1)当C，D两点都在线段OA上且OC=OE时，求证：AC=OD；

(2)若抛物线y2与线段AB没有交点，求m的取值范围.

思路：

(1)证明y2的对称轴为x=－2即可，即证明m=2；

(2)分两种情况，分别建立模型，求解。

解读：

抛物线y1的顶点A(－4，0)，与y轴交点B(0，－4)，则直线AB为y=－x－4；抛物线y2=x^2＋2mx＋n=(x＋m)^2＋n－m^2的顶点P(－m，n－m^2)在抛物线y1上，因而

n－m^2=－1/4(4－m)^2，

解得n=－1/4(4－m)^2＋m^2=(3m^2＋8m－16)/4=(m＋4)(3m－4)/4

(1)线段OA：y=0，且0≤x≤－4，

抛物线y2的对称轴：直线x=－m(图中直线PQ)，垂直平分线段CD是必然的，当点C，D在线段OA上时，对称轴PQ必然也垂直线段AB，能否平分AB，则要看m的取值是否为－2。

如图PQ⊥AB，垂足为Q(－m，0)，则－4≤－m≤0，所以0≤m≤4，

抛物线y2开口向上，穿越x轴负半轴，则抛物线y2的顶点P必在第三象限，与y轴的交点E(0，n)必在y轴的正半轴，此时n＞0，即此时OE=n，

当OC=OE=n时，点C(－n，0)，因而当x=－n时，y2=0，

即n^2－2mn＋n=0，因为此时n＞0，所以n=2m－1，

又因为n=(3m^2＋8m－16)/4

所以(3m^2＋8m－16)/4=2m－1，解得m=2，m=－2，又0≤m≤4，所以m=2，

此时垂足Q(－2，0)，所以Q为既为OA的中点，也是CD的中点，因而AC=OD.

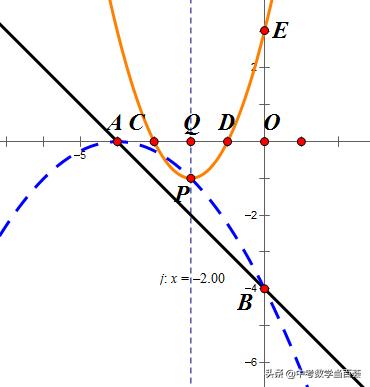
(2)抛物线y2与线段AB没有交点，有两种情况：

情况1：抛物线y2与直线AB没有交点；

情况2：抛物线y2与直线AB有交点，但交点不在线段AB上。

情况1意味着方程x^2＋(2m＋1)x＋n＋4=0没有实数根，

即△=(2m＋1)^2－4(n＋4)= (2m＋1)^2－(3m^2＋8m－16)－16

=(m－2)^2－3＜0，解得2－√3＜m＜2＋√3

因而情况1时，2－√3＜m＜2＋√3

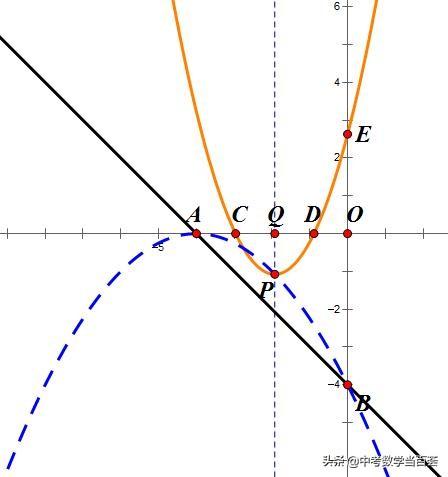
情况2抛物线y2与直线AB有交点，但交点不在线段AB上。

抛物线y2与直线AB有交点，交点不在线段AB上，

意味着又有下面两种情况

情况21 (如图)

△≥0，且yE＞－4

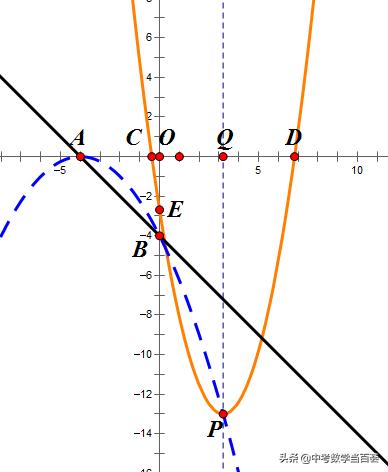
△=(m－2)^2－3≥0，

解得m≤2－√3或m≥2＋√3

yE=n=(3m^2＋8m－16)/4＞－4

m(3m＋8)＞0

解得m＜－8/3或m＞0

综合得m＜－8/3或m≥2＋√3

情况22 (如图)

△≥0，且xP＜－4

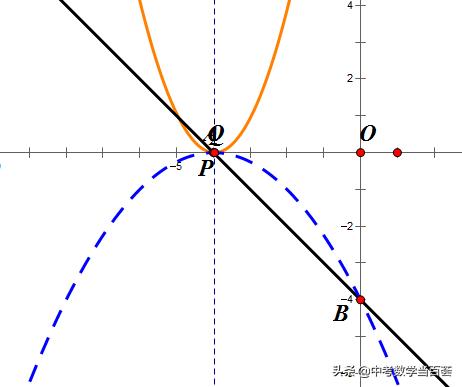
△=(m－2)^2－3≥0，

解得m≤2－√3或m≥2＋√3

xP=－m＜－4

即m＞4

综合得m＞4

当m=4时，抛物线y2顶点P与A重合，不符合题意，

因而情况2时，m＜－8/3或m≥2＋√3且m≠4

综合情况1，2得

m＜－8/3或m≥2－√3且m≠4，

所以若抛物线y2与线段AB没有交点，则m＜－8/3或m≥2－√3且m≠4.

综述：

根据交点情况，确定参数。

1.按常规方法，先求出交点横坐标(方程的解)，再根据交点范围，列出不等式，求解即可。但列出的不等式往往是分式，二次根式复合体，非常复杂，求解不等式并不容易。所以常规方法，建模易，求解难；

2.特殊方法，借助图象，考虑交点相对于指定区间的两端的特殊位置，建立模型，列出不等式，求解。该法求解相对容易，但建模不易。

3.各种情况参数范围的汇总也是难点，初中学段没学集合，更没学集合的运算交并补，因而很难理解：情况内(且)求交，情况间(或)求并。

---

关注“中考数学当百荟”，感谢您的点赞，转发！点击“了解更多”

---