犀牛给曲线增加控制点_Rhino犀牛「一张面建模-02」——浅析蛋壳面的几种做法...

Rhino犀牛本文将对一张面生成贝壳面的几种做法做一个简单的分析。

在许多产品中都会使用到蛋壳面，最经典的想必就是苹果电脑了。(当然它并不是用文中的方式建的，他的建模更加的精细复杂)

​

运用一张面建模构建贝壳面的方式大致有三种，以如下图造型为例。

方法一

首先绘制一个平面。

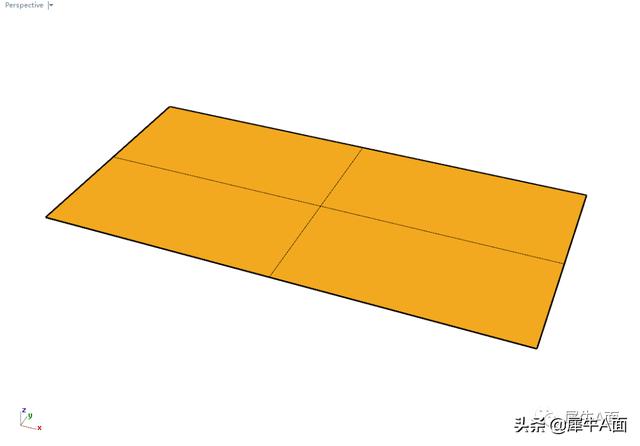
将曲面重建为uv均为5阶6点。

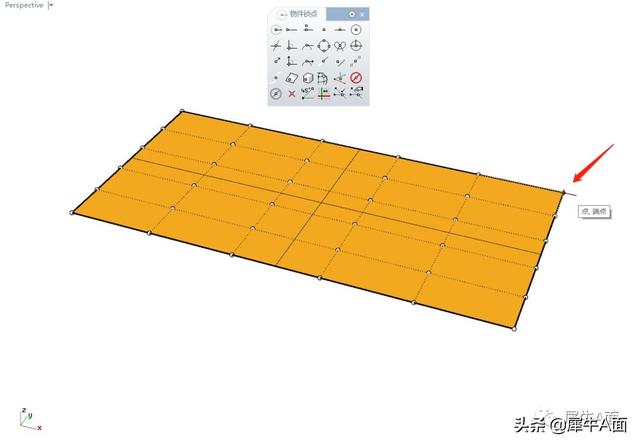
使用物件锁点工具栏中的“两点间”指令，将这块面的角点移动到其相邻两个控制点重点

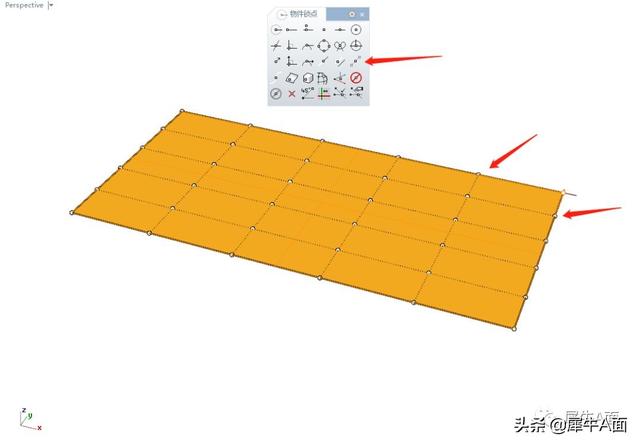
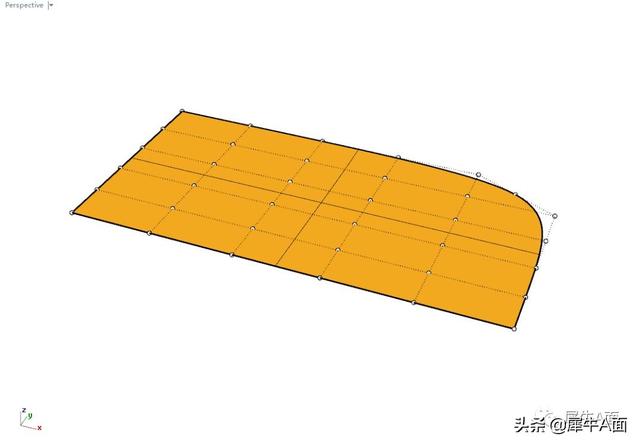
对4个角点进行同样操作。

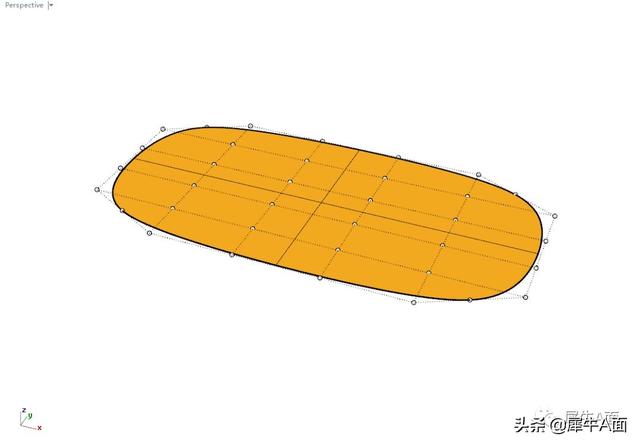
选取除边界之外的控制点。

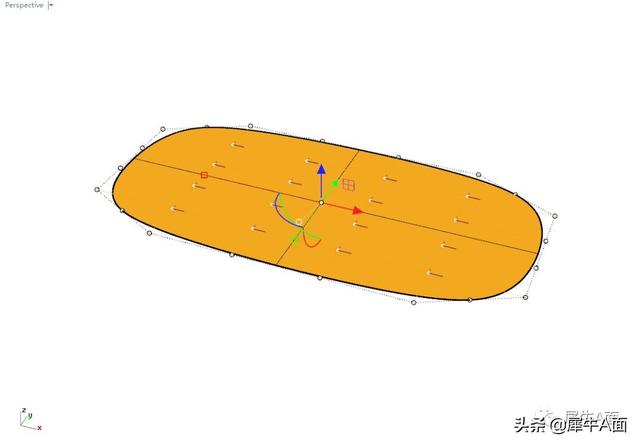
使用操作轴向上拖动合适距离。

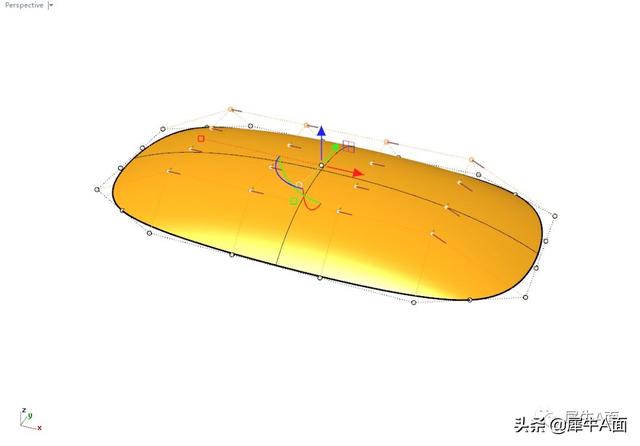
调整控制点来控制造型,构建完成。

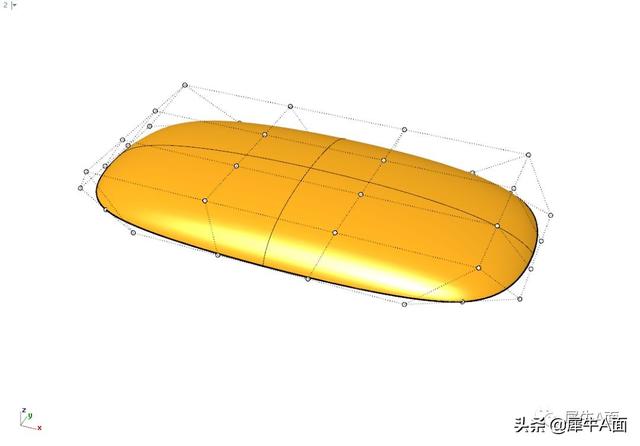
方法二

绘制一侧的一条边界曲线

镜像后打开其编辑点。

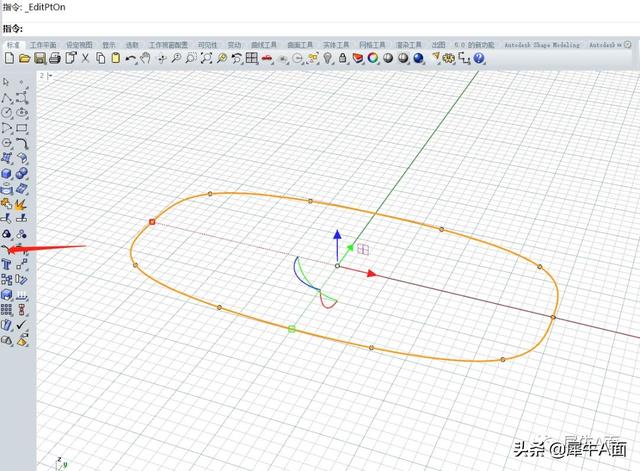
以相对应的编辑点为端点，绘制截面线。

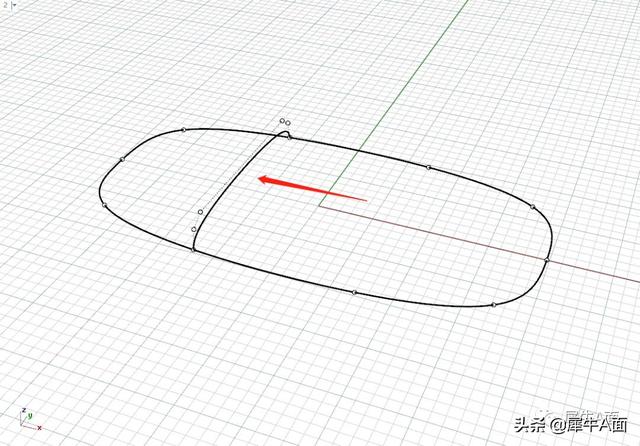
使用双轨扫掠命令，分别选择轨道线和截面线。

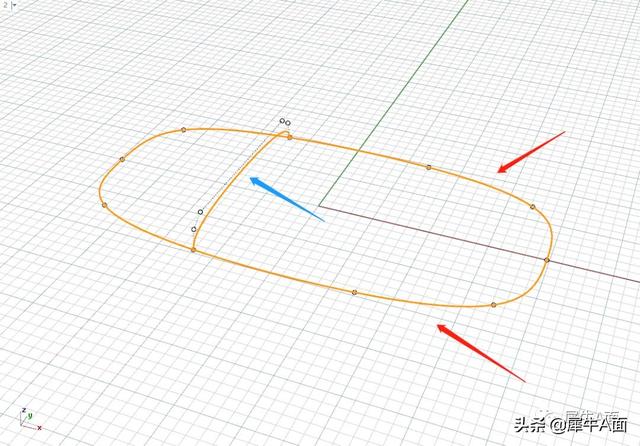
勾选最简扫掠。

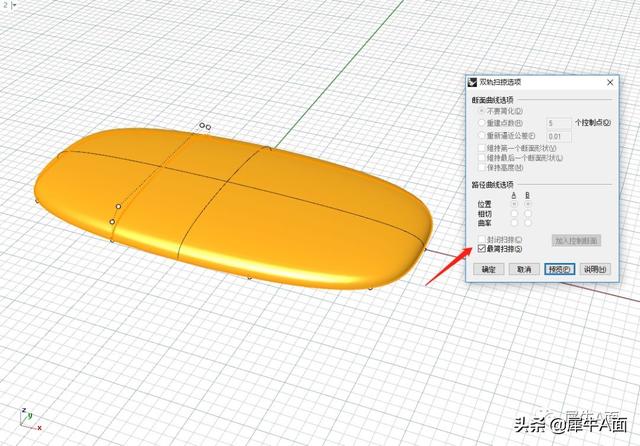
得到如下控制点的曲面

调整控制点来控制造型,构建完成。

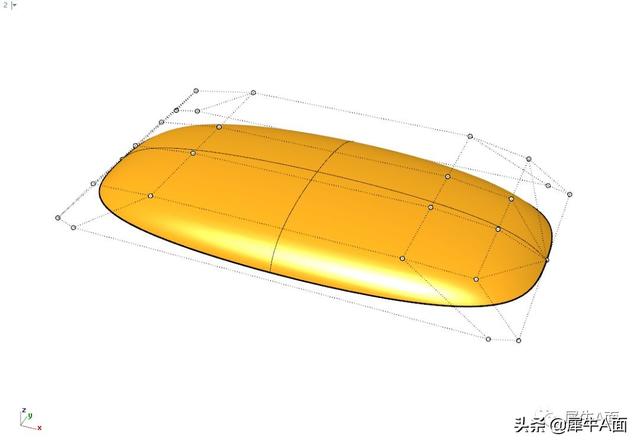
首先来看方法一和方法二是如何生成的贝壳面具备怎么样的结构，众所周知，曲面一般都是具有uv方向，所以具有4边结构。

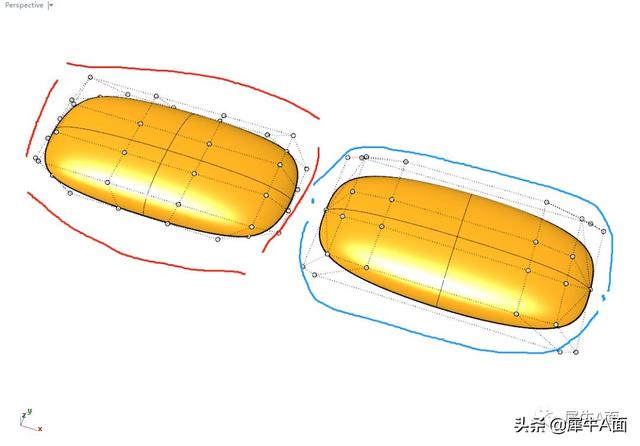
方法一的4边结构相对均匀的分布。

方法二的4边结构中其中两边退化成为一个点。

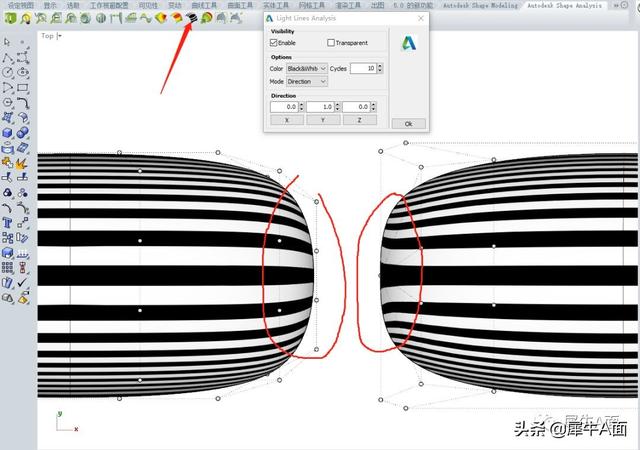
打开vsr的固定斑马线查看效果。

显然方法一的斑马更为顺畅，方法二的斑马在端点处不够好(大部分情况调整控制点无法优化这个问题)。

那是因为方法一的4个边界分布的更为均匀，而方法二的其中两条边被聚集到一个点上了，所以会发生这样的问题。

有的朋友看到这里会说，那方法一既好调整，又不会在边界处发生斑马线的弯折，是不是就是用来做一张面贝壳面的最好方法呢，并不一定是！

适合用来的做造型的方法，需要用多个维度来评价。

通过上述对这两者的描述：

曲面效果，方法一胜出。

接下来是边界造型描述的准确度和便捷性角度。

方法一由于4边分布均匀，导致角点“退化”成了边缘的“倒角”，导致实际需要两条曲面的相接来控制倒角处的造型，这样的控制方式，对于新手来说是不友好的。

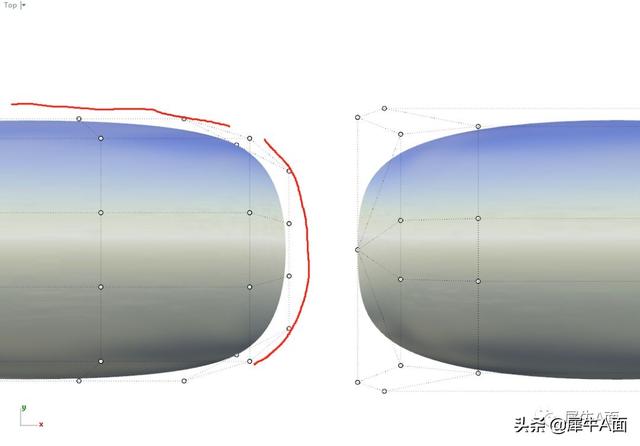
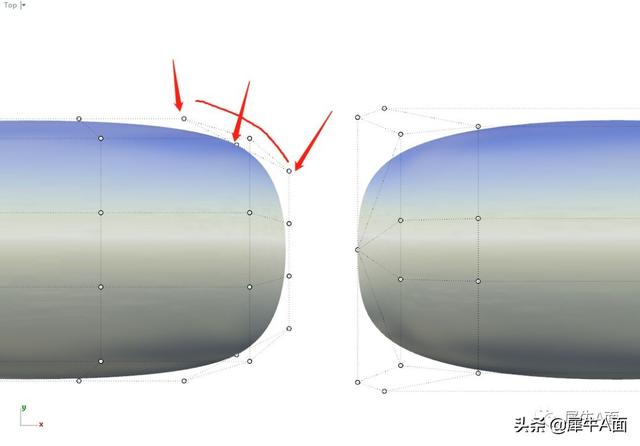
方法二的边界则直接是由一条贝塞尔曲线控制，曲线能够保持高度顺滑，并且更直观，更易于调整。

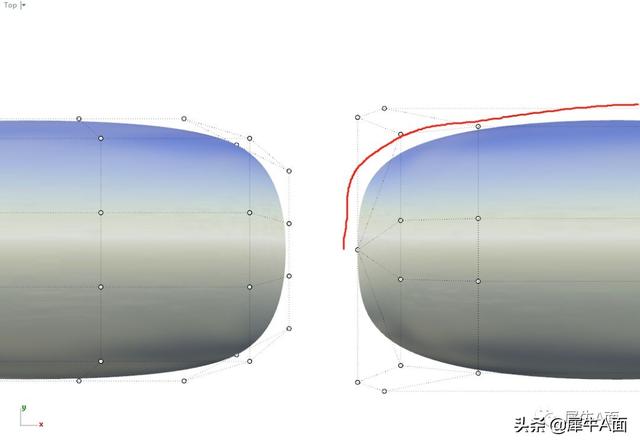
边界造型描述的准确度和便捷性角度方法二略胜于方法一。

第三个维度从曲面的“对称性”维度来判断(我也不知该怎么形容，姑且看下去)

在做与自身对称的形态时，方法一就显得很无力了，完全无法描述“对称性”了。因为其中一个控制点分身乏术，无法控制这个区域的相切性。如下图所示(这里可能需要动手做一遍理解起来会更容易)。

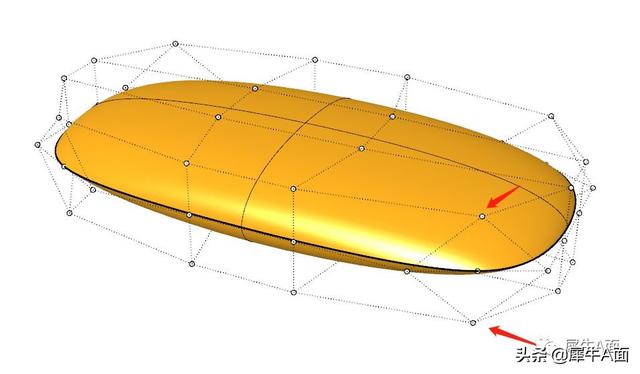
方法二就完全没有这种问题，具有完美对称性。

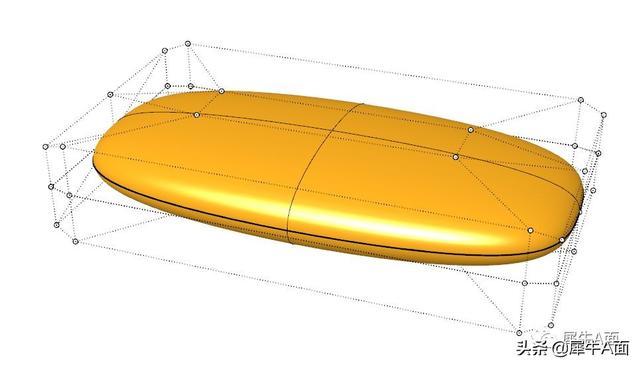
曲面的“对称性”维度，方法二完胜方法一。

看了这么，大家也许会问，方法三藏了这么久是不是，有它有更好的解决方法，看下去~

方法三

绘制轨道线和截面线。

然后使用“RailRevolve”指令，(沿路径旋转，旋转命令的右键就是这个指令)。

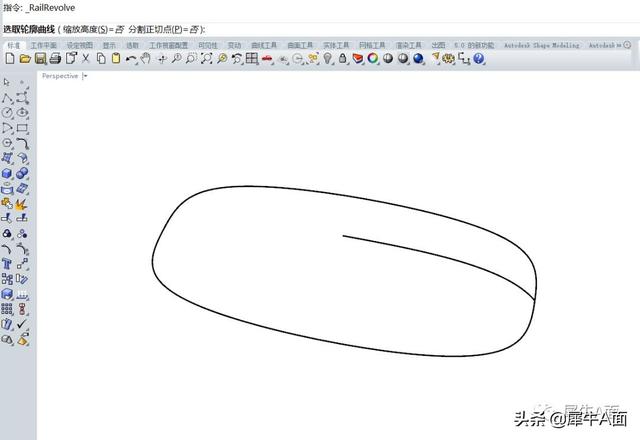
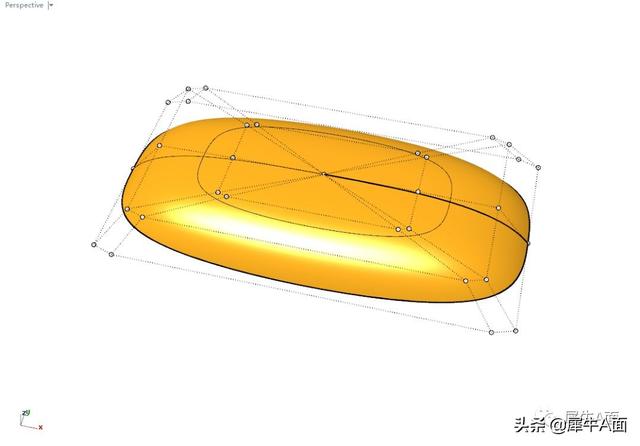
怎么说这个方法额，对于轨道线和截面线都可以有精准的描述，但是，曲面内部的可调整性不够好，而且曲面上有两条合并在一起的边缘线，有时候可能无关紧要，但是模型复杂之后进行分割、布尔运算时，会把曲面分割成多个面。

在对曲面内部连续性有要求不高的时候，可以使用这种方式。

高质量曲面基本不会采用这种方式，因为这种结构调高质量面需要花费更多的时间。

结尾为大家归纳一下：

方法一：对于有一定曲面经验、造型要求自由度大、单张面时会有更好的效果。

方法二：实用性最好，角落处的瑕疵可以通过后续手段弥补。

方法三：对于质量要求不高且造型规律、明确的曲面的快速构建，有很高效率。

希望通过这期一张面建模系列之蛋壳面浅析，加强大家对曲面的理解，这样哪怕是做超高精度、真正标准精确的蛋壳面一样可以游刃有余。