pythonarma模型t检验_【描述时序】趋势、季节和随机性

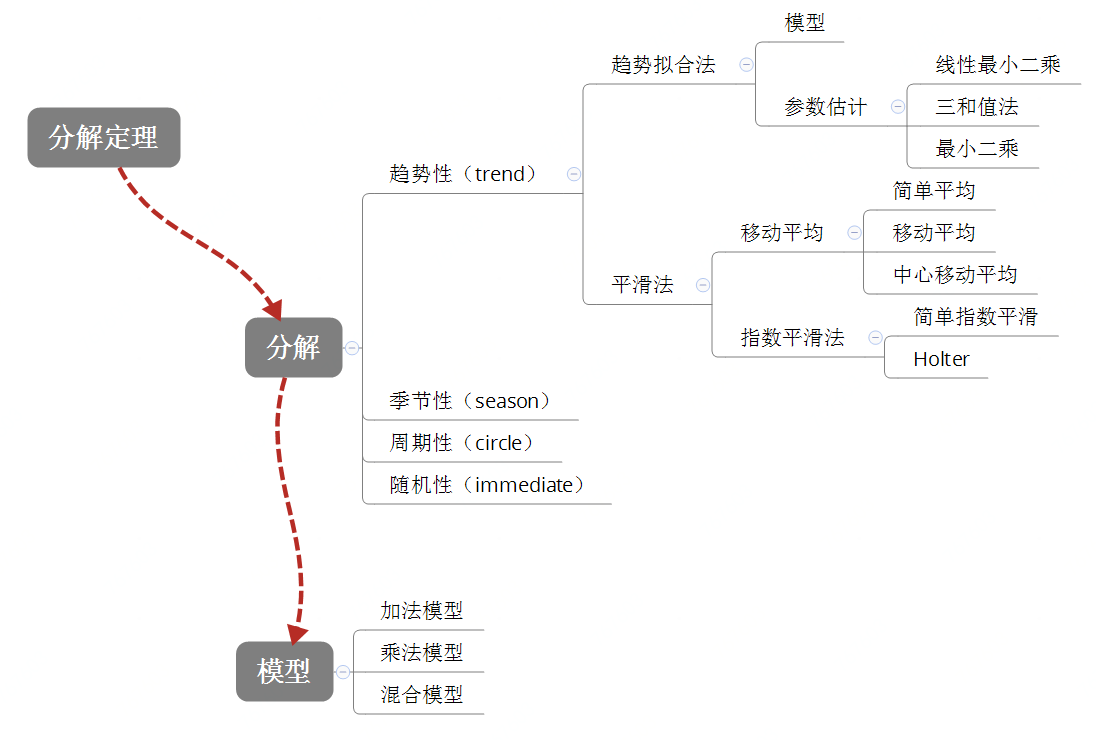
先看此知识体系：

1. 分解

1.1 分解定理

wold分解定理

(1938)

任何一个离散平稳过程$x_t$都可以分解为两个不相关的平稳序列之和，其中一个为确定性的，另一个为随机性的。

$x_t=V_t+\xi_t$

其中，

$V_t$是确定性序列

$\xi_t=\sum\limits_{j=0}^\infty \phi_j \varepsilon_{t-j}$是随机序列

$\phi_0=1,\sum_{j=0}^\infty \phi_j^2

$\varepsilon_t\sim N(0,\sigma_\varepsilon^2)$，也就是白噪声序列

$E(V_t,\varepsilon_s)=0,\forall t\neq s$

下面定义什么事 确定性序列 和 随机性序列

$y_t=a_0+a_1y_{t-q}+a_2y_{t-q-1}+…+v_t$

$v_t$是残差，定义$\tau_q^2=Var(v_t)$

如果$\lim\limits_{q\to\infty}\tau_q^2=0$，那么$y_t$叫做确定性序列

如果$\lim\limits_{q\to\infty