等比例放大或缩小 背景图片_小学数学知识点大全（三）：比和比例

一、比的认识

1、生活中两个量之间存在倍比关系。

2、两个数相除，又叫作这个两个数的比。

3、读写法：

在两个数的比中，中间的是比号，比号前面的数是比的前项，比号后面的数是比的后项。比的前项、后项可以是分数、小数、整数或具体的数量，2：3 , 0.3：0.2, 30米:20千米 都是比.

连比：三个或三个以上的数的关系也可以用比来表示，例如：一个长方体的长、宽、高的比是3：4：5，这样的比叫作“连比”。

4、以下三种“比”的不同：

(1)体育比赛中的2比0，这里的“比”只是记录比赛双方得分的一种形式，表示一方得2分，另一方得0分。

(2)20比15多5。这里的“比”是一种加减关系。

男生人数4人，女生人数是3人，男生人数与女生人数的比是4：3，这里的比就是我们数学中要学的比，表示的是男生与女生人数的倍比关系。它表示男生人数是(接图)

(3)甘蔗汁与 水体积 比 是 1：2 水与甘蔗汁的体积比 是 2：1。

(4)“路程”与“时间”的比的“比值”表示的是“速度”。比值越大，速度越快，比值越小，速度越慢。

“总价”与“数量”的比 的“比值”表示的是“单价”。比值越大，商品越贵，比值越小，商品越便宜。

7、“比、分数、除法”的关系

比的前项相当于分子，被除数，比号相当于分数线，除号，比的后项相当于分母，除数。

比值相当于分数值、商。

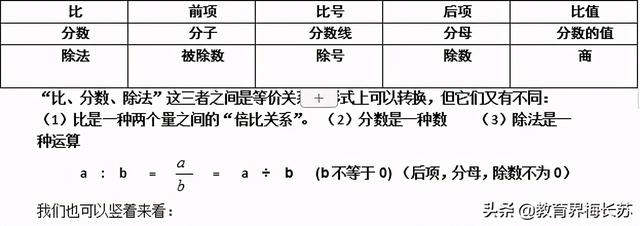
分子 前项 被除数

分数线 比号 除号

分母 后项 除数 (不0)

分数的值 比值 商

8、(1)比的基本性质：比的前项或后项同时乘或除以相同的数(0除外)，比值大小不变，这叫作“比的基本性质”。(比)

(2)商不变规律：被除数与除数同时乘或除以相同的数(0除外)，比值大小不变，这叫作“商不变规律”。(除法)

(3)分数的基本性质：分子与分母同时乘或除以相同的数(0除外)，分数的大小不变，这叫作“分数的基本性质”。(分数)

9、把一个比 化成 最简 整数比 的过程叫“化简比”或“比的化简”。

比的化简的结果叫“最简比” 用a:b形式表示。最简比的前项与后项的数是互质数，只有公因数1。

10、比的化简：

(1)“整数比”的化简：

“整数比”改写成“分数”，化成最简分数，最后改写成“比的形式” a:b。

(2)“小数比”的化简：

移动小数点，把“小数比”改写成“整数比”，再按“整数比”化简的方法“化简”。

(3)“分数比”的化简

前项除以后项，商用“最简分数”表示，最后改写成“比的形式” a:b。

11、“比值”与“比的化简”的区别

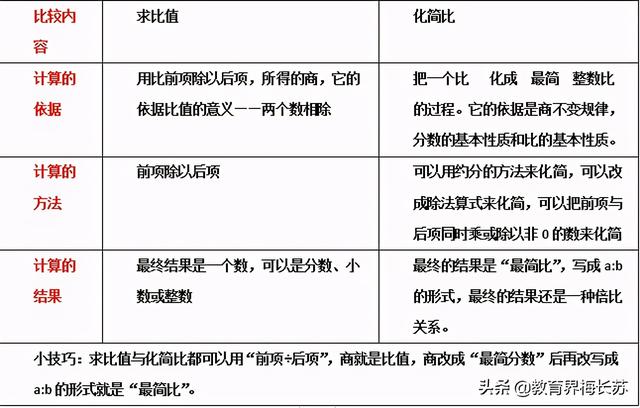
12、比的应用：

(1)按一定的比进行分配的意义：在工农业生产和日常生活中，常常需要把一个数量按照一定的比进行分配，这种分配方法通常叫作：按一定的比进行分配。

(2)按一定的比进行分配问题的解法：

方法一：分数法：先求出总份数，再找出部分量占总量的几分之几，最后用分数乘法计算。

方法二：平均法：先求出总份数，再求出每一份的数量，最后用每一份的数量乘部分量对应的份数。

(3)按比分配的应用题：

求“每一份的数量”：

做比的应用题，关键还是找出每一份的数量

每一份的数量=总量÷总份数

每一份的数量=部分量÷部分量对应的份数

每一份的数量=前后项相差的数量÷前后项相差的份数

二、比例的认识

1、比例的意义：表示两个比相等的式子叫作比例。

2、比例各部分的名称：组成比例的四个数叫作比例的项，其中两端的两项叫作外项，中间的两项叫作内项。

3、比例的基本性质：在比例里，两个外项的积等于两个内项的积。

4、判断两个比是否成比例的方法：

(1)计算两个比的比值，看是否相等。(2)利用比例的基本性质，外项积等于内项积。

三、比例尺

3、比例尺的相关公式

(1)图上距离÷实际距离=比例尺(根据比例尺写出图上距离和实际距离的比，统一单位，再化简比。)

(2)图上距离÷比例尺=实际距离

(3)实际距离×比例尺=图上距离

4、根据比例尺画图的方法：根据方向、角度、距离，用量角器画图

(1)观测点与量角器中心重合(2)第一方向与0刻度线重合(3)根据第二方向确定旋转的方向。(4)标点、连线。(画线段，写角度、距离，地方名称。)(5)标比例尺

5、解比例：在比例中，如果已知比例中的三项，都可以求出这个比例中的另外一个未知项。求比例中未知项的过程，叫作：解比例。解比例是解方程中的一种。

6、解比例的方法：根据比例的基本性质， 先把比例转化成外项的积与内项的积相等的形式，也就是方程，再解方程，求出未知项的值。

7、图形的放大与缩小：

(1)图形按一定的比放大或缩小，要使放大或缩小前后图形的对应的线段长度的比相等。

(2)按一个图形放大或缩小后所得到的图形与原图相比，形状相同，大小不同。

(3)按一定比放大图形，比的前项的数字更大，比的后项的数字更小(4：1)。按一定比缩小图形，比的前项的数字更小，比的后项的数字更大。(1：4)

(4)公式：放大前的长度×比例尺=放大后的长度 缩小前的长度×比例尺=缩小后的长度

(5)按一定的比把图形放大或缩小时，放大或缩小的是图形的相关线段的长度，而不是图形的面积。所以，图形的放大或缩小是用图形每条边的长度与乘除比例尺，一般不用面积或体积去乘除比例尺。

(6)按一定比放大或缩小图形，应该考虑图形的横、竖、斜线的变化。

三、正反比例

1、生活中的存在着许多有关系的变化的量。这些变化的量存在着相互依存的关系，一个量变化，另一个量也随着变化，一个量的值确定，另一个量的值也随之确定。

4、正、反比例图象：正比例图象是一条直线，反比例图象是一条曲线。

5、判断成正比例与反比例的方法：(1)找变量，确定两个量是相关联的量。(2)看定量：看两种量之间的关系是比值(商)一定，还是积一定。

6、用正比例、反比例解决实际问题步骤：

(1)分析数量关系，判断这个应用题是成什么比例。

(2)设未知数为X。

(3)找等量关系：如果是成正比例，就按列比例的方程，如果成反比例，就列乘法的方程。

(4)解方程，检验并写答。