正方形里面两个扇形相交部分_华杯赛试题，求阴影部分的面积，后附类似题目方法总结...

如图，梯形ABCD的面积是117平方厘米，AD//BC，EF=13厘米，MN=4厘米，又已知EF⊥MN于O，请问阴影部分的总面积为多少平方厘米？

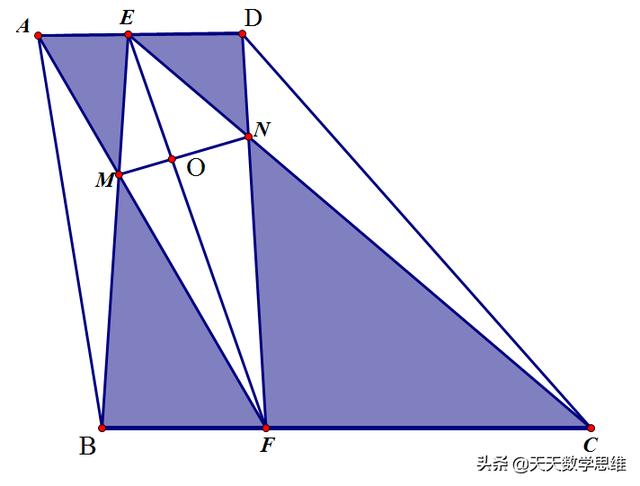
[思路导航] 这是一个普通的梯形，看起来图形略复杂，知道了梯形总面积和线段EF与MN长度以及关系，如果考虑用梯形面积减去左右三角形和中间四边形的面积的方法不太好办

---

仔细观察中间的四边形EMFN正好是△ADF与△BCE重叠的部分，

如果能求出这两个三角形面积的和用容斥原理就可以求出阴影部分面积

将图分解一下

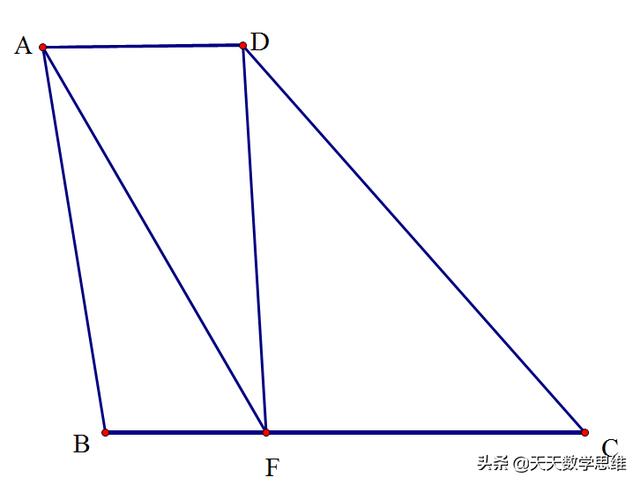
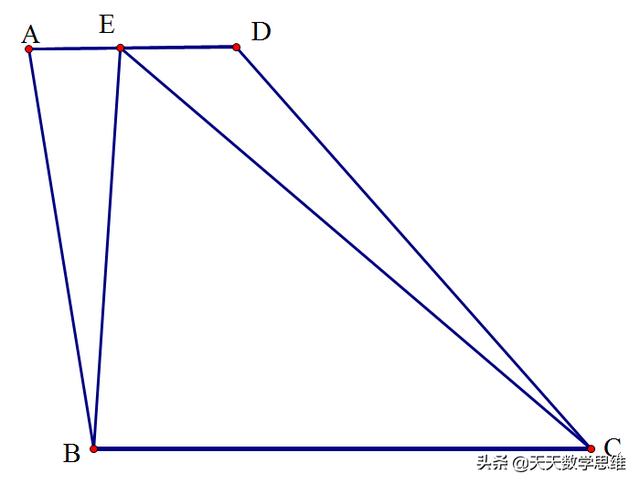
我们记梯形的高为h

S梯＝(AD+BC)*h/2

S△ADF=AD*h/2， S△BCE=BC*h/2

即：S梯＝S△ADF+S△BCE

所以

S阴影＝117－13*4/2*2=65平方厘米

小结：这是一道典型的用容斥原理求面积的问题，这样的方法在扇形与三角形或四边形组合的题目中也经常使用，当图形比较复杂时需要适当分解成各种图形再根据图形情况进行计算。

---

---

类似题目

1、 (华杯赛试题)如图中，六边形ABCDEF的面积是2010平方厘米．已知△ABC，△BCD，△CDE，△DEF，△EFA，△FAB的面积都等于335平方厘米，6个阴影三角形面积之和为670平方厘米．求六边形GHMNPQ的面积

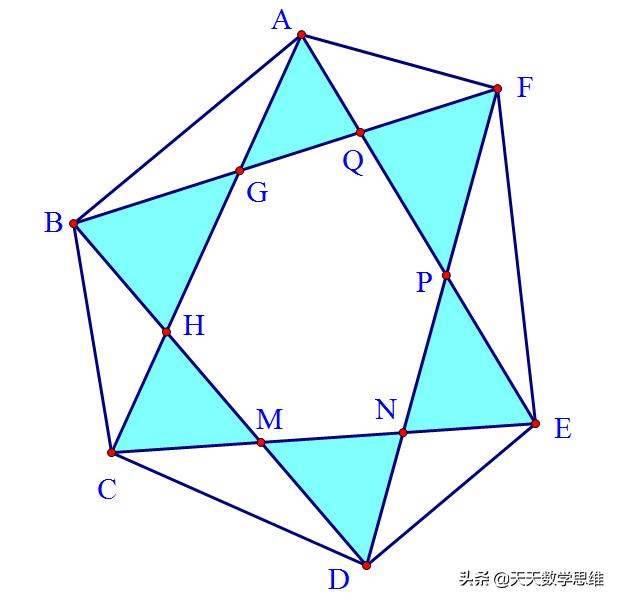
解：因为条件中的六个三角形的面积之和是

335*6＝2010(平方厘米)

正好是条件中六边形的面积

而阴影部分是这六个三角形不重叠的部分

说明阴影面积之和正好等于小六边形GHMNPQ的面积

S六边形GHMNPQ＝670平方厘米

---

---

2、如下图求阴影部分面积(用含π式子表示)

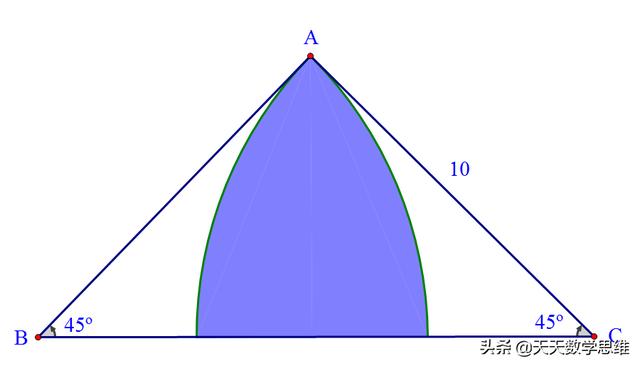
这是一个基本模型，拆开我们可以得到下图

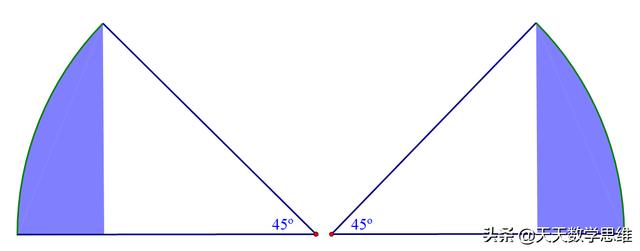
阴影部分是两个八分之一扇形重叠部分

用两个扇形之和减去原图中的等腰直角三角形即可

S阴影＝10*10π/4-10*10/2=25π-50

---

---

3、 如图、矩形ABCD的长宽分别是6和3，求阴影部分面积(用含π式子表示)

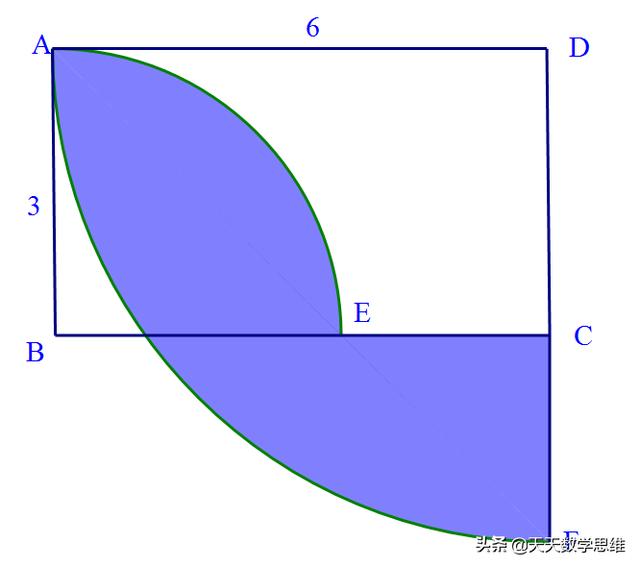
解：阴影部分可以看成两个半径不同的四分之一圆面积之和减去长方形的面积

S阴影＝3*3π/4+6*6π/4-3*6=45π/4-18

---

---

4、 如图、三角形的一条边长是6，求阴影部分面积(用含π式子表示)

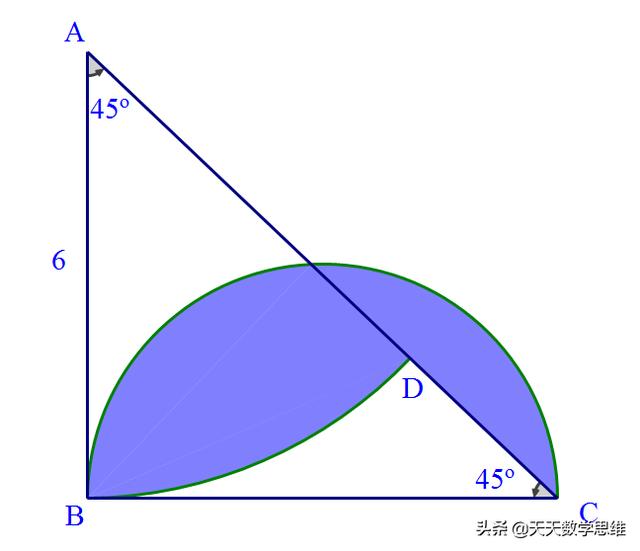
解：根据重叠情况，阴影面积是八分之一圆加上半圆减去三角形

S阴影＝6*6π/8+3*3π/2-6*6/2=9π-18

---

---

5、如图，平行四边形的长边是6短边是3，高为2.6，求阴影部分面积(用含π式子表示)

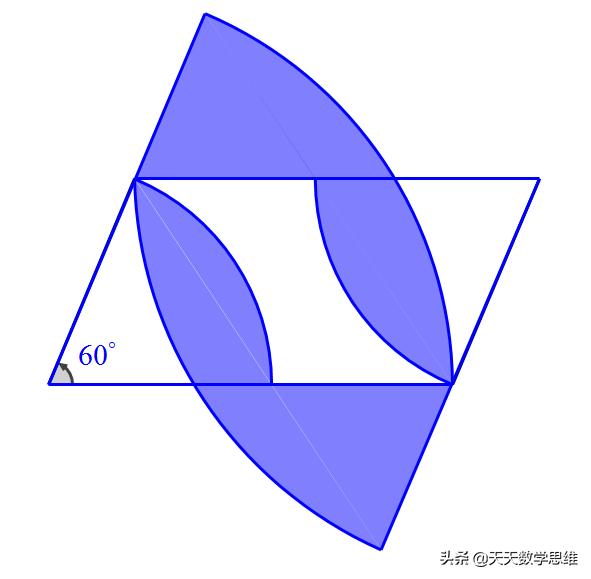
解：这也是一个典型的容斥原理图形，我们标示如下

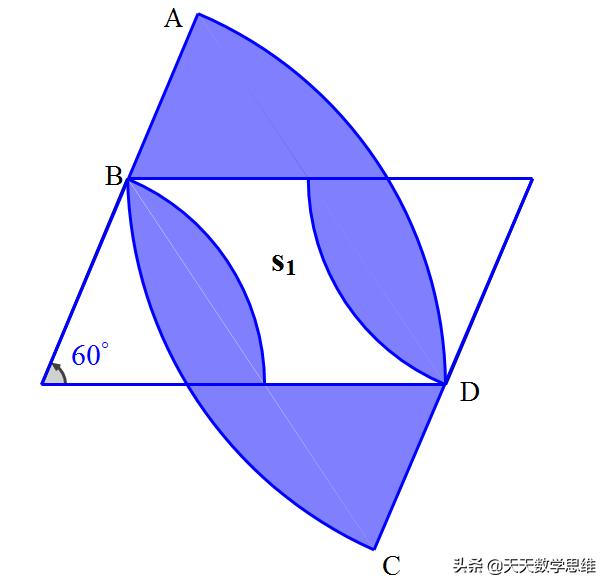
分析 ：

阴影面积用曲四边形ABCD的面积减去S1即可

曲四边形ABCD的面积是两个半径为6的扇形减去平行四边形

S1的面积是用平行四边形减去两个半径为3的扇形

S阴影＝6*6π/3-2.6*6*2+3*3π/3=15π-31.2

---

---

6、已知正方形的面积是100，求阴影部分面积

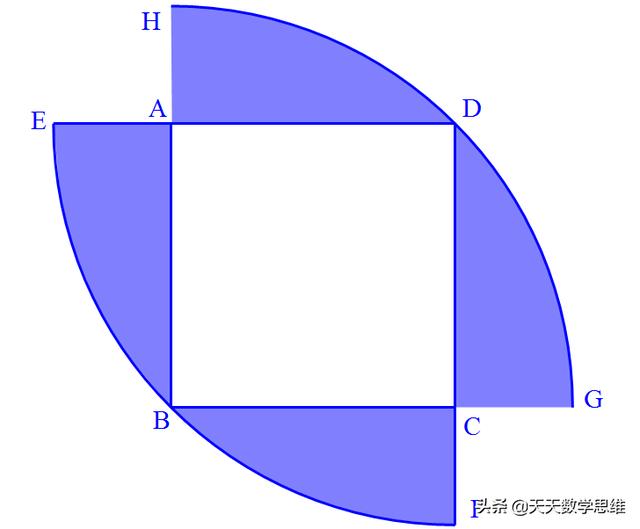
用半圆减去两次正方形面积即可