mandelbrot集 matlab,再谈Julia集与Mandelbrot集

很早以前，我简单介绍过 Julia 集和 Mandelbrot 集，文章在此。这可以说是数学中最神秘、最令人敬畏的研究对象之一。不过，那时我对这个话题了解还不太深。今天见到这个网页，让我对 Julia 集和 Mandelbrot 集有了更深的了解。我查阅了一些其他的资料，然后写下这篇长文，与大家一同分享。继续阅读以前，建议先看看我原来那篇文章(很短)，那里面有很多漂亮的 Julia 集和 Mandelbrot 集的图片，这篇文章就不再展示了。

还是让我们先来简单复习一下复数吧。由于承认“负数也能开平方”将会带来很多幽雅和便利的结论，因此我们发明了虚数，用 i 来表示 -1 的平方根(即虚数单位)，并把实数扩展为复数(即一切形如 a + b i 的数)。正如实数可以用数轴上的点来表示一样，复数可以用平面直角坐标系上的点来表示。令 x 轴表示复数的实数部分，令 y 轴表示复数的虚数部分，则 a + b i 就对应了平面上的点 (a, b) 。我们把这个平面直角坐标系叫做“复平面”。

复数与复数之间不但可以相加相减，还可以相乘相除。(a + b i) + (c + d i) 就等于 (a + c) + (b + d) i ，而 (a + b i) (c + d i) 则等于 (ac – bd) + (bc + ad) i 。需要注意的是，我们不能讨论一个复数乘以另一个复数后是变大了还是变小了，因为复数根本没有大小之分。如果真的要比较它们的大小，我们可以比较它们的模。复数 a + b i 的模就是 a2 + b2 的平方根，也就是它到复平面原点的距离。如果我们用不同的颜色来表示不同大小的模，那么整个复平面大致就是这样：

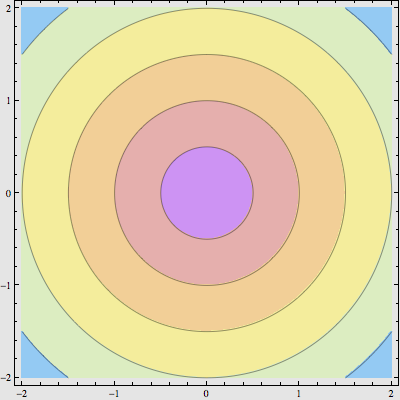
如果我们用 |z| 来表示复数 z 的模，那么上面这个图也就是函数 f(z) = |z| 的“等高线地图”。复数的模有一个重要的性质，大家可以自行验证：乘积的模等于模的乘积，即 |a·b| = |a|·|b| 。现在，我们对复平面上的所有点都进行平方，画出 f(z) = |z2| 的等高线地图：

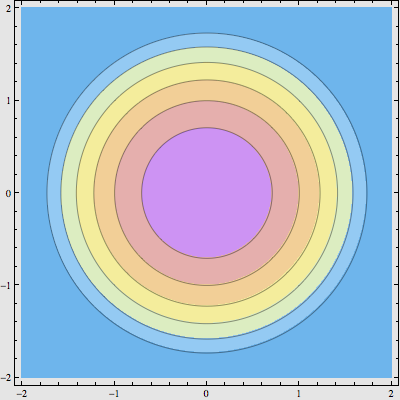
可以看到，这一操作让模的变化更剧烈了，等高线变得更加密集了。外面浩瀚的蓝色空间，就对应着那些模已经相当大了的复数。

有趣的事情开始了。如果对上图中的每个点再加上某个数，比如 0.3 ，那么整个图会怎样变化呢？容易想到，对于模相同的复数来说，给实数部分加上 0.3 ，这对实数部分本来就较大的数影响会更大一些。因此，上图将会变得更扁，整个图形会在水平方向上压缩。这也就是 f(z) = |z2 + 0.3| 的等高线地形图：

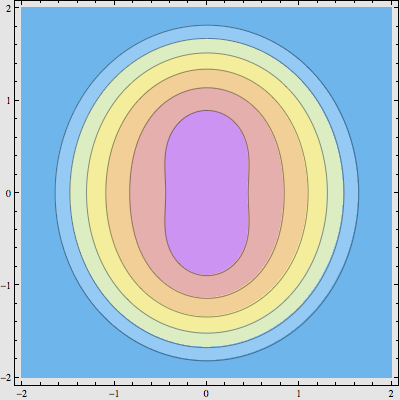
接下来，我们再对所得的图形进行平方，继续加剧模的变化：

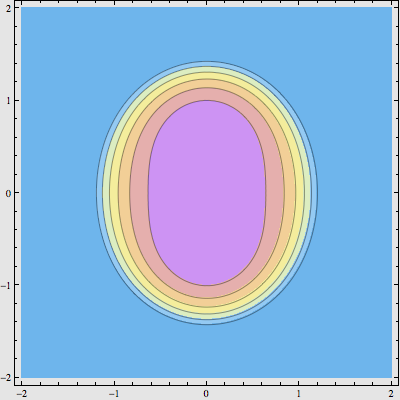
然后，再给每个点的实数部分加上 0.3 ，于是得到 f(z) = |(z2 + 0.3)2 + 0.3| 的图像：

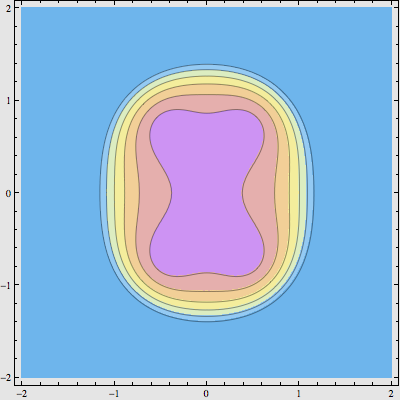
再平方：

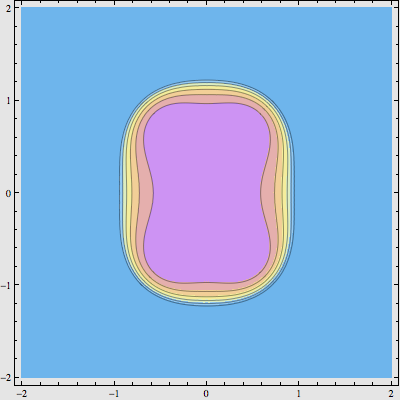
再加上 0.3 ，此时图形已经开始变得有意思起来了：