动点四边形周长最短_利用几何画板探寻中考热点动点最值问题

最近几年的中考对动点最值问题十分热，也是让考生最感头疼的问题。这不仅考察学生的数学想象力，同时也是对数学思维变化的一个综合检验。图形在动点的运动过程中观察图形的变化情况，需要理解图形在不同位置的情况，才能做好计算推理的过程，在变化中找到不变的性质是解决数学动点探究题的基本思路。这也是动态几何数学问题中的最核心的数学素养。动点问题往往涉及到到动点的轨迹，而动点的轨迹究竟是一个什么样的图形，这才是动点问题的一个核心问题。

动点问题主要的数学思想基本上是：分类讨论思想，函数思想，方程思想，数形结合思想，转化思想。

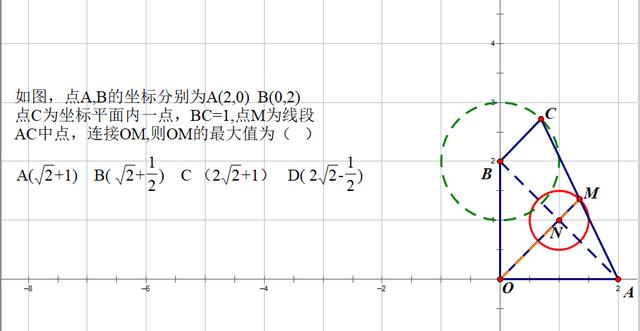
案例一：德州市2020年中考数学选择题压轴试题(中考数学中，一般选择题12道，第12题压轴；填空6道，第18题压轴；大题7道，第25题压轴)

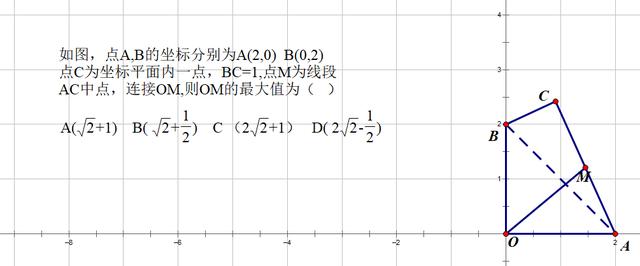
本题的得分率十分低，基本上无人做对。究其原因，还是无法通过变化寻求不变，探寻出M点的轨迹。

对于此题我用几何画板先把M点的轨迹探寻出来

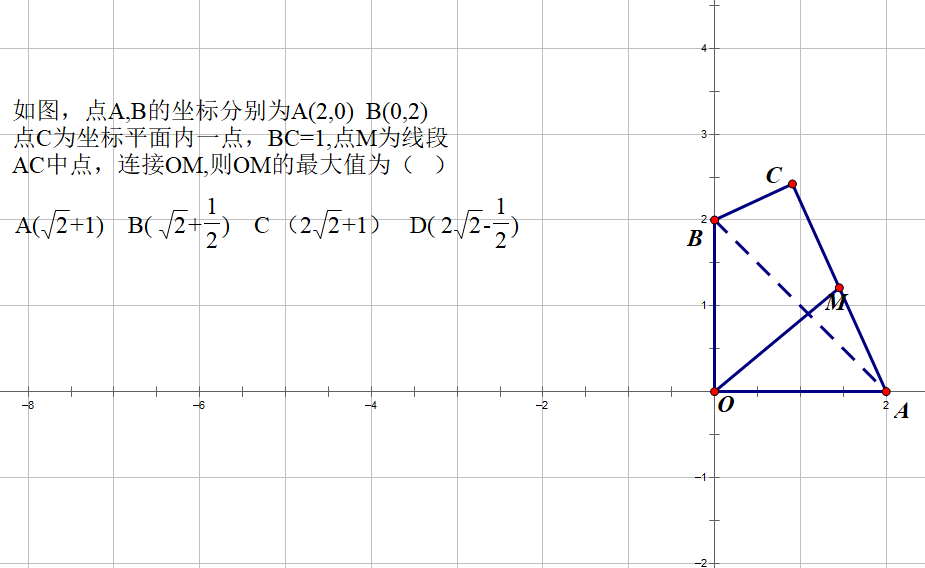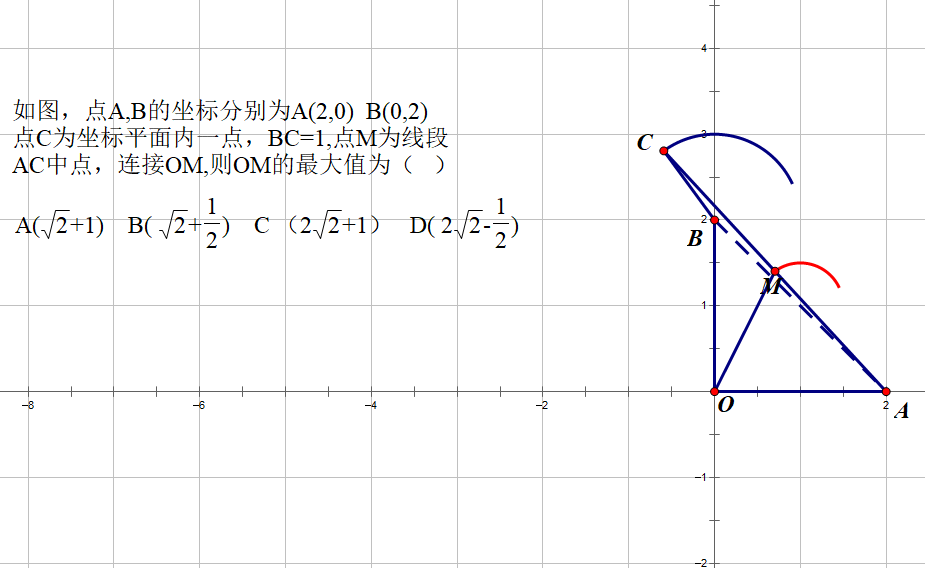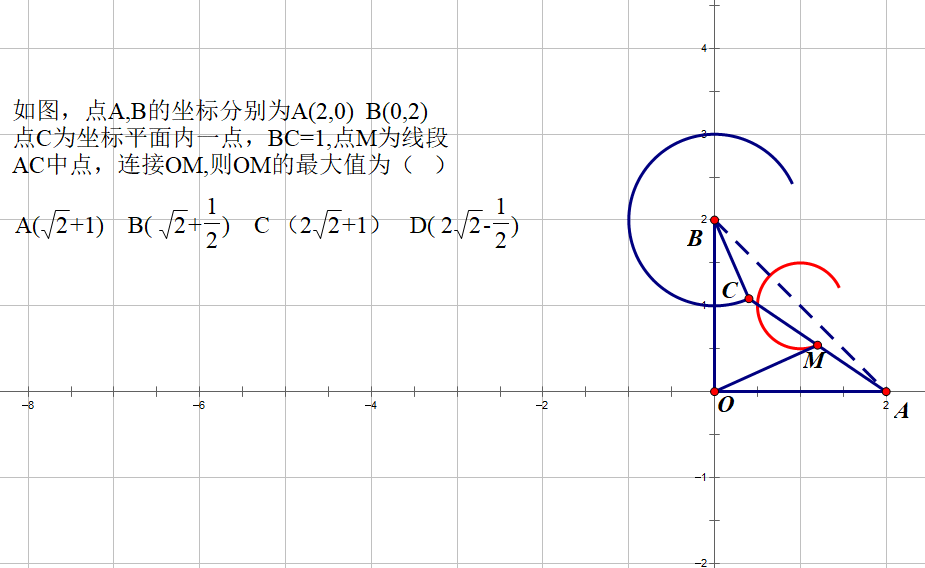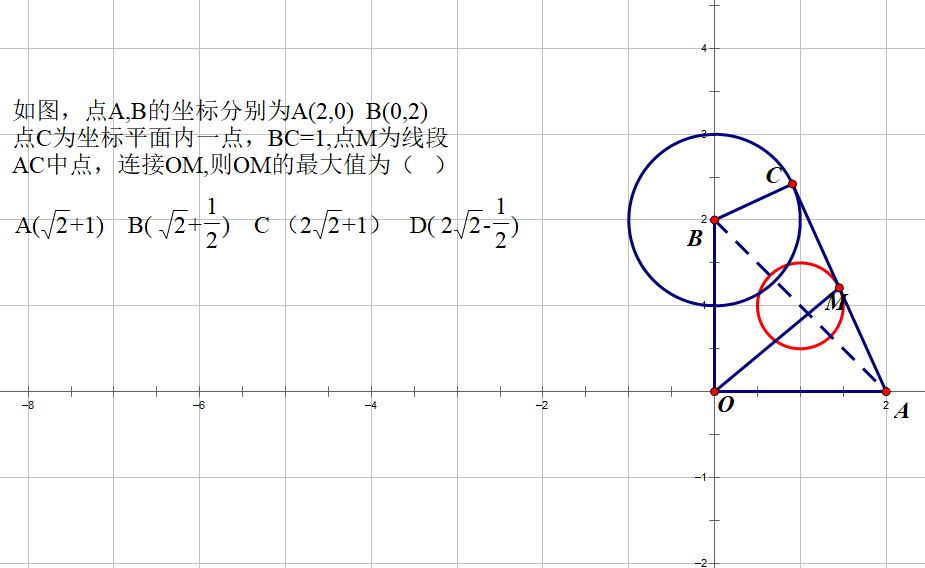
不难发现，M点的轨迹是一个圆。在考场上没有几何画板软件，就需要通过动点C，不断的寻找特殊点，通过动手画图，去寻找M点位置，然后，根据M点位置的变化，来想象推理出M点的轨迹。

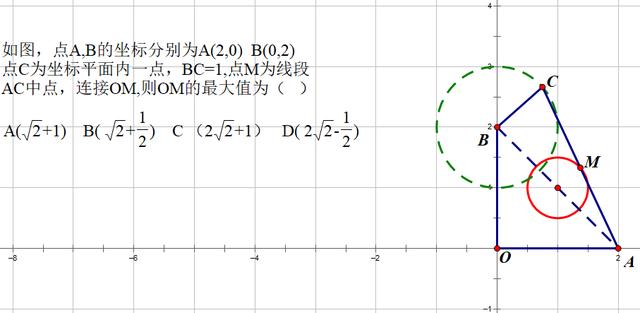
由于BC是定值，C点是平面一点，可以确定C点到B(定点)的距离不变，由此推断出C点的运动轨迹是一个圆，在C点的运动过程中，M点也会随之发生变化，通过不断的绘图操作，可以发现M点的轨迹也是一个圆。

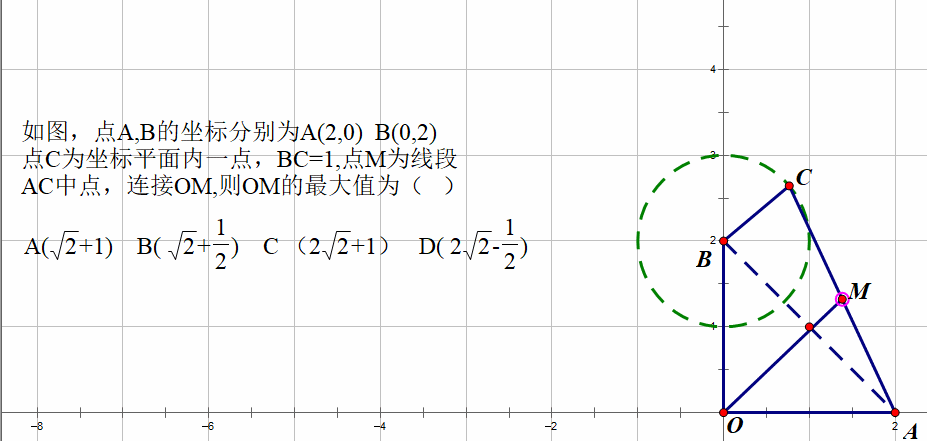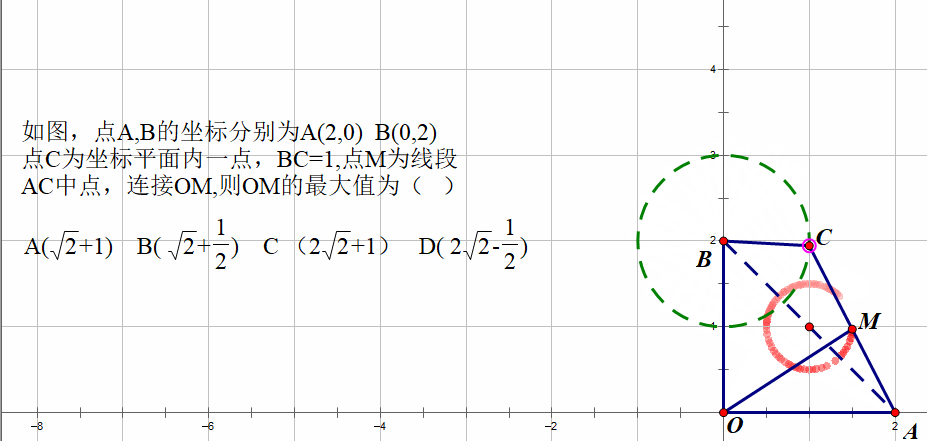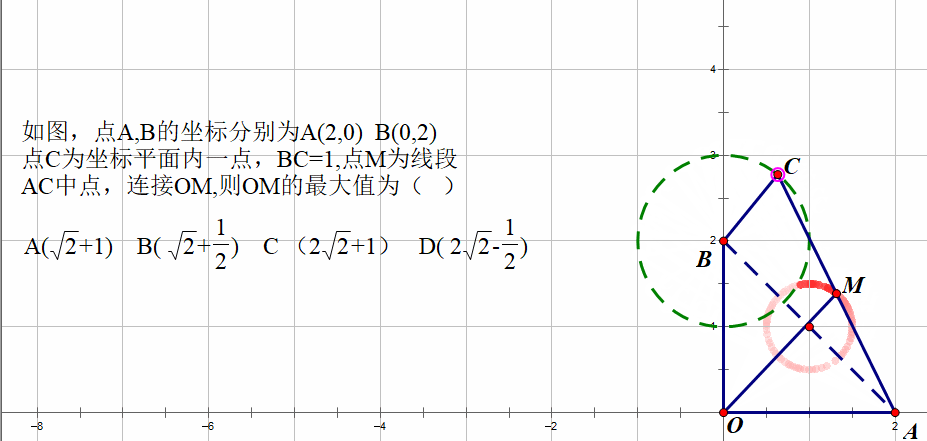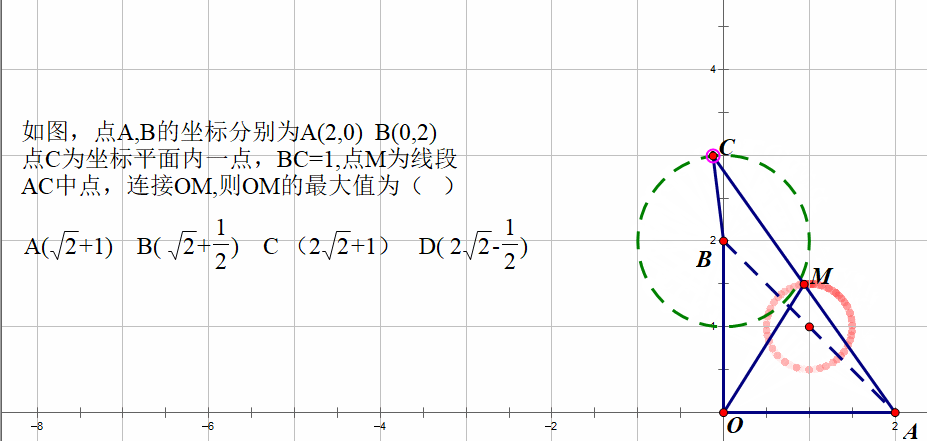
现在重点是探寻这个圆的圆心的问题。

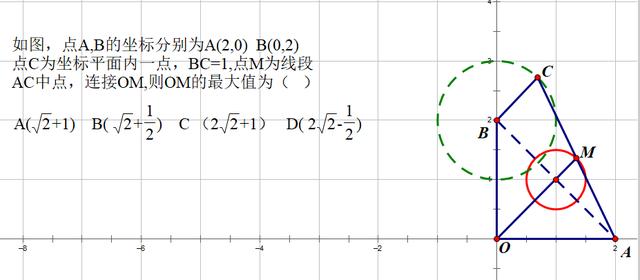
我们知道圆心必须是一个定点，那么在C点的运动过程中，M点到哪个点的距离始终保持不变，这是本题的第二个关键点。

通过探寻不变量，我们依据M点的中点性质，很容易就发现圆心是AB中点，BC是定值，所以只有BC所在三角形的中位线才是不变的。

至此，现在我们就开始研究第三个关键点：什么时候OM最大。

我们连结轨迹圆的圆心N与M，NO，发现，无论是M点在何位置，都存在ON+OM>OM。

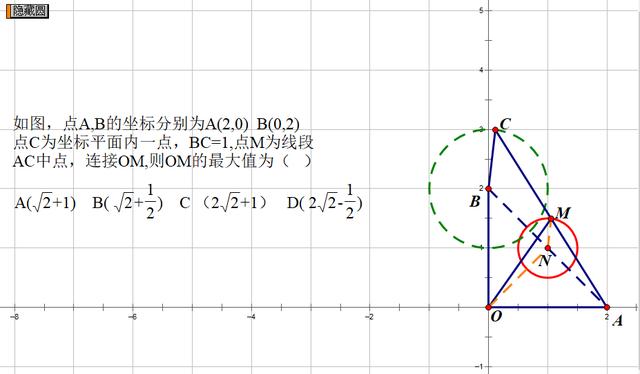
也就是只有ONM三点共线时，OM才是最大的。

这也符合圆外一点到圆上点最长距离的证明。

当推理到这里时，已经不难求出ON=AB/2 NM=BC/2 从而推出OM的最大值应该选B

案例二：

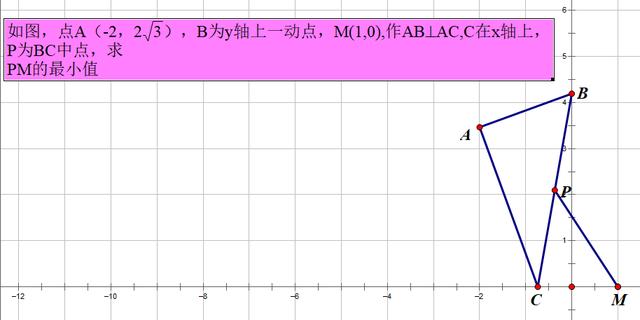
此题不难看出P点是被动点B带动的，所以我们可以改变B点 的位置，通过多画几个图来寻找P点的位置，从而推理P点的轨迹。

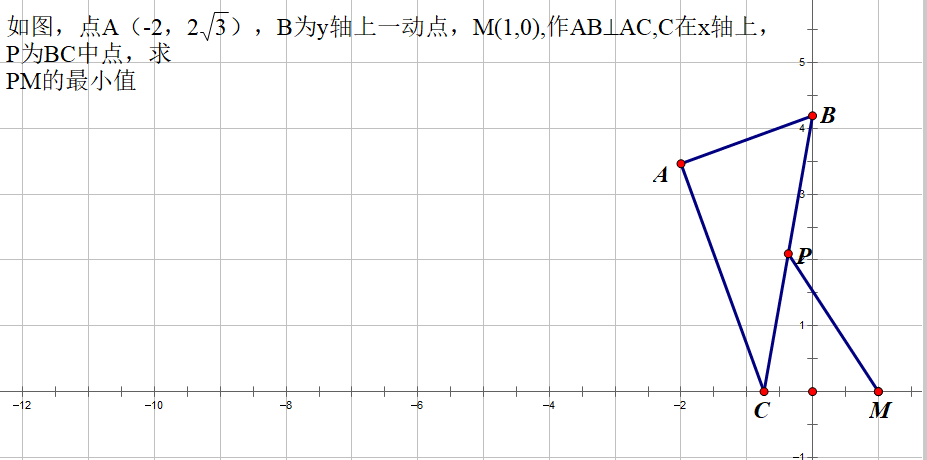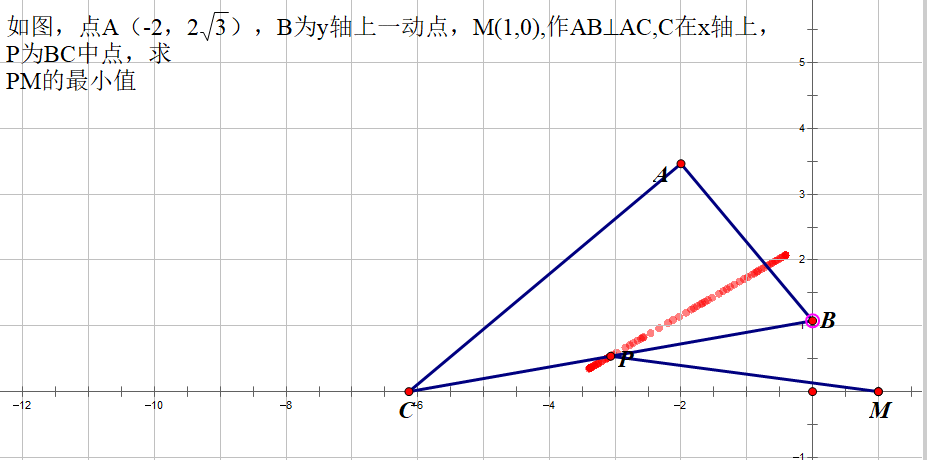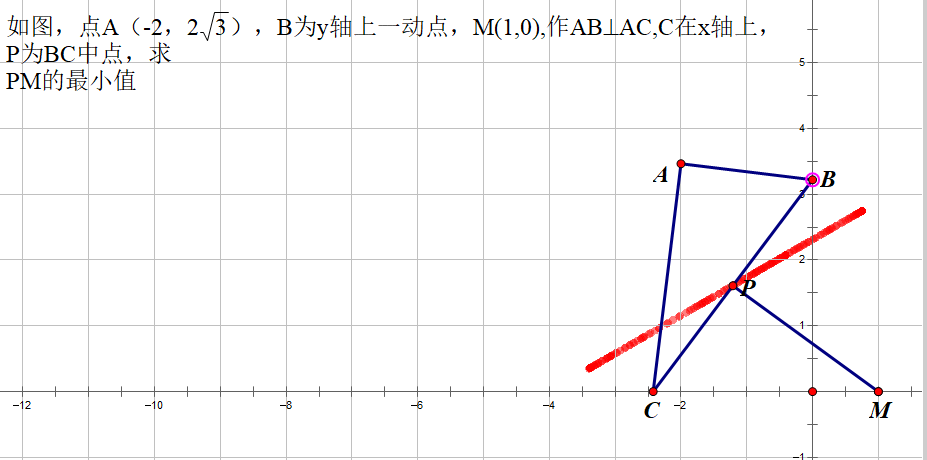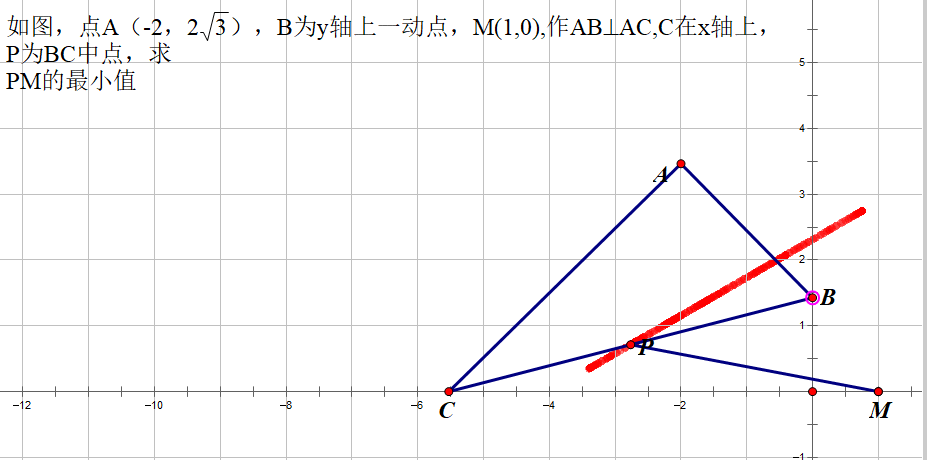
通过几何画板追踪点的轨迹，不难发现P点的轨迹是一条直线。

这样求PM最短也就是求M点到直线的最短距离——垂线段

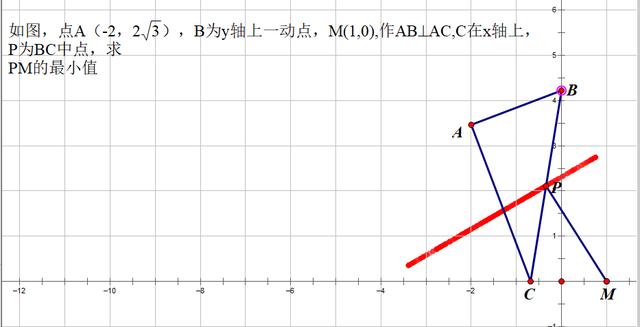
动态几何的绘图，一般是由特殊到一般，先让动点移到几个特殊点，画出图形，然后，根据被动点的位置来寻找被动点的轨迹。所以要把握好一般与特殊的关和纱，分析过程中，特别要关注图形的特性(特殊角，特殊图形的性质、图形的特殊位置等)。动点问题一直是中考的热点，近几年考查探究动动中的特殊性：等腰三角形，直角三角形，相似三角形，平行四边形，梯形，特殊角或其三角函数，线段或面积的最值。