dtft频移性质,数字信号处理最新章节_原萍著_掌阅小说网

2.1 非周期序列的傅里叶变换(DTFT)

与连续非周期信号一样，离散时间非周期信号的频域分析涉及到傅立叶变换(也就是信号的谱)。傅里叶变换揭示了时域与频域之间的关系，本质上是建立以“时间”为变量的信号和以“频率”为变量的频谱函数之间的变换关系，下面讨论离散时间信号的傅里叶变换。

2.1.1　DTFT的定义

离散时间信号的傅里叶变换也用DTFT(Discrete Time Fourier Transform)来表示，其定义为

其中，ω为数字频率，单位是弧度(rad)。X(e

jω

)代表信号的频率内容，换句话说，它是信号x(n)的频率(正弦或余弦)分解。

DTFT成立的充分条件是序列x(n)绝对可和，即满足下式：

用e

jωm

乘式(2.1)两边，并在-π～π内对ω积分，同时考虑虚指数函数的正交性得

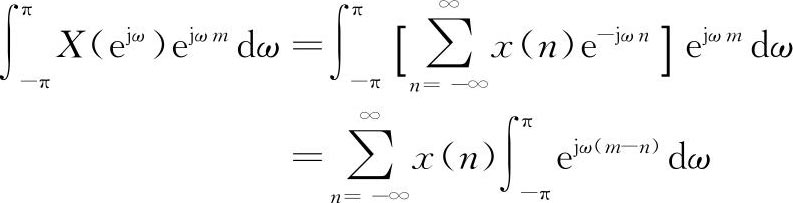
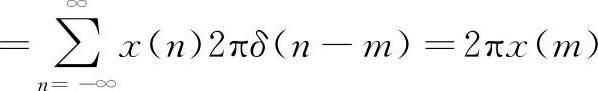
将上式的m用n替换，因此

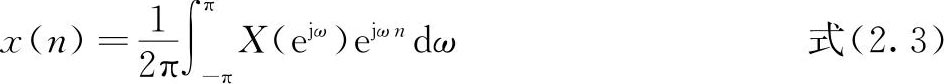
上式即是DTFT的反变换。式(2.1)和式(2.3)是一对傅里叶变换，叫做序列的傅里叶变换对。

【例2.1】

设x(n)=R

N

(n)，求x(n)的DTFT。

解

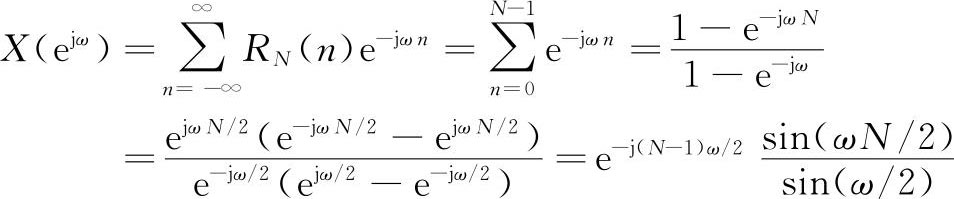
当N=4，X(e

jω

)的幅度与相位随ω变化曲线(幅度谱和相位谱)如图2.1所示。

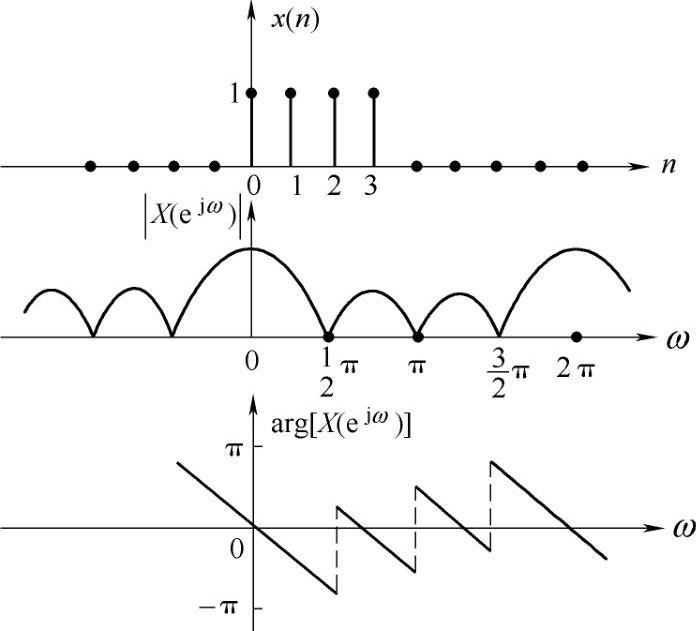
图2.1　R

4

(n)幅度谱和相位谱

2.1.2　DTFT的性质

1.DTFT的周期性

在定义式(2.1)中，n取整数，因此下式成立：

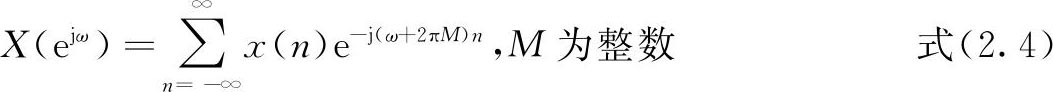
因此，序列的傅里叶变换是频率ω的周期函数，周期是2π。对比连续信号的傅里叶变换，它同样表示了信号在频域的分布规律，但不同的是序列的傅里叶变换是以2π为周期的函数。在ω=0和ω=2πM附近的频谱分布应是相同的，在ω=0，±2π，±4π，…点上表示x(n)信号的直流分量，那么离开这些点愈远，其频率应愈高，但又是以2π为周期，那么最高的频率应是ω=π。还要说明的是，所谓x(n)的直流分量，是指如图2.2(a)所示的波形。例如，x(n)=cosωn，当ω=2πM，M取整数时，x(n)的序列值如图2.2(a)所示，它代表其直流分量；当ω=(2M+1)π时，x(n)波形如图2.2(b)所示，它代表最高频率信号，是一种变化最快的信号。由于DTFT的周期性，一般只分析±π之间或0～2π之间的DTFT就行了。

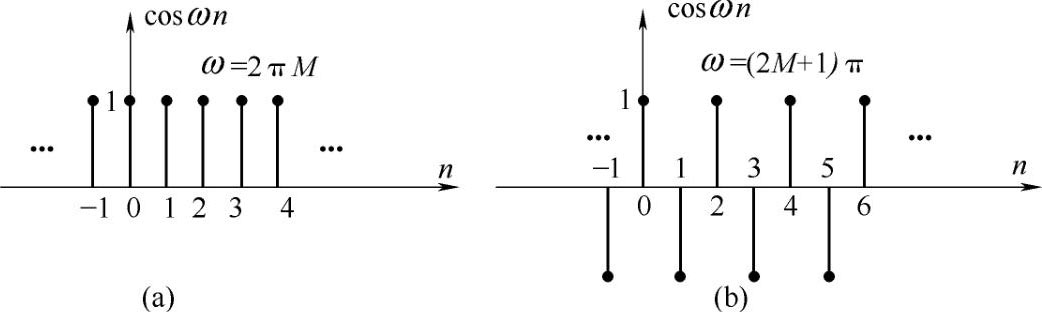
图2.2　cosωn的波形

2.线性性

设X

1

(e

jω

)=DTFT[x

1

(n)]，X

2

(e

jω

)=DTFT[x

2

(n)]，那么

DTFT[ax

1

(n)+bx

2

(n)]=aX

1

(e

jω

)+bX

2

(e

jω

)

式(2.5)

式中a，b为常数。

傅里叶变换可以视为是对信号的一种运算，它是一个线性变换，线性性使得它适用于线性系统的分析。

3.时移性

设X(e

jω

)=DTFT[x(n)]，那么有

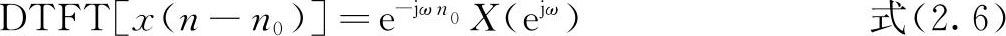
这个性质意味着一个信号在时域移动n

0

个采样，而它的幅度谱不变，只是相位谱改变了-ωn

0

。

4.频移性

设X(e

jω

)=DTFT[x(n)]，那么

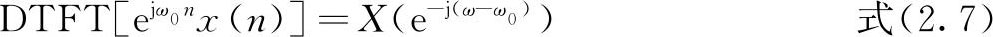
5.对称性

在学习DTFT的对称性以前，先介绍什么是共轭对称与共轭反对称及其它们的性质

设序列x

e

(n)满足下式：

则称x

e

(n)为共轭对称序列。当共轭对称序列是实数时，式(2.8)变为x

e

(n)=x

e

(-n)，即x

e

(n)为偶对称序列。为研究共轭对称序列具有什么性质，将x

e

(n)用其实部与虚部表示：

x

e

(n)=x

er

(n)+jx

ei

(n)

将上式两边n用-n代替，并取共轭，得到：

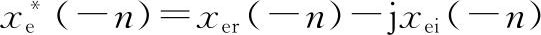
对比上面两公式，因左边相等，因此得到：

x

er

(n)=x

er

(-n)

式(2.9)

x

ei

(n)=-x

ei

(-n)

式(2.10)

由上面两式得到共轭对称序列其实部是偶函数，而虚部是奇函数。类似地，可定义满足下式的共轭反对称序列：

当共轭反对称序列x

o

(n)是实数时有x

o

(n)=-x

o

(-n)，即x

o

(n)为奇对称序列。将x

o

(n)表示成实部与虚部x

o

(n)=x

or

(n)+jx

oi

(n)同样可以得到：

x

or

(n)=-x

or

(-n)

式(2.12)

x

oi

(n)=x

oi

(-n)

式(2.13)

即共轭反对称序列的实部是奇函数，而虚部是偶函数。

【例2.2】

试分析x(n)=e

jωn

的对称性。

解

将x(n)的n用-n代替，再取共轭得到：

x

*

(-n)=e

jωn

因此，x(n)=x

*

(-n)，故x(n)是共轭对称序列，如展成实部与虚部，得到：

x(n)=cosωn+jsinωn

上式表明，共轭对称序列的实部确实是偶函数，虚部是奇函数。

任意一个序列总可以表示成一个共轭对称和共轭反对称序列之和，即

其中，

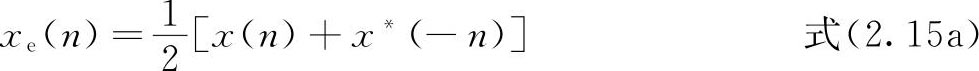
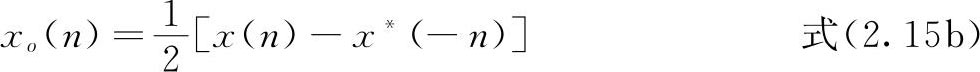
同理，对于频域函数X(e

jω

)，也有和上面类似的概念和结论，即

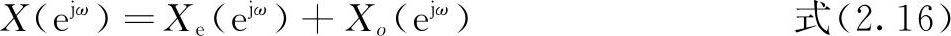
式中，X

e

(e

jω

)与X

o

(e

jω

)分别为共轭对称分量和共轭反对称分量，它们满足：

同样有下面式子：

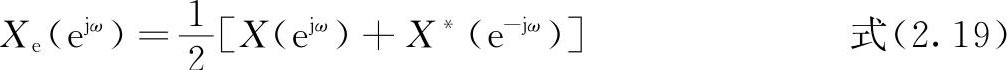
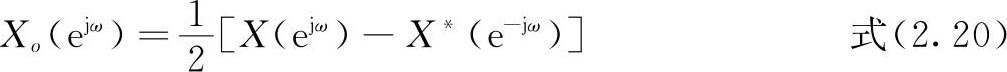
由以上的定义，可以得到DTFT的对称性了，下面按两部分进行分析。

(a)将序列x(n)分成实部x

r

(n)与虚部x

i

(n)，即

x(n)=x

r

(n)+jx

i

(n)

将上式进行DTFT，得到

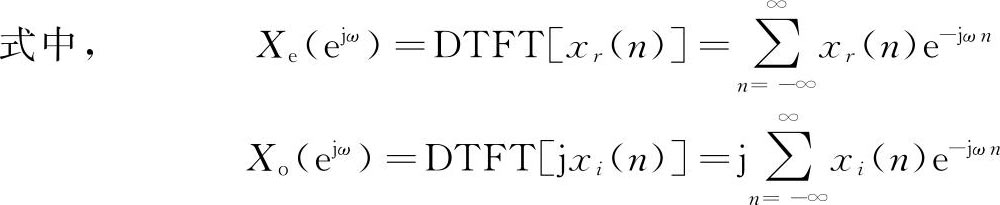
上面两式中，x

r

(n)和x

i

(n)都是实数序列。容易证明：X

e

(e

jω

)满足式(2.17)，具有共轭对称性，它的实部是偶函数，虚部是奇函数；X

o

(e

jω

)满足式(2.18)，具有共轭反对称性质，它的实部是奇函数，虚部是偶函数。

最后得到结论：序列分成实部与虚部两部分，实部对应的DTFT具有共轭对称性，虚部和j一起对应的DTFT具有共轭反对称性。

(b)将序列分成共轭对称部分x(n)和共轭反对称部分x

o

(n)，即

x(n)=x

e

(n)+x

o

(n)

将式(2.15)重写如下：

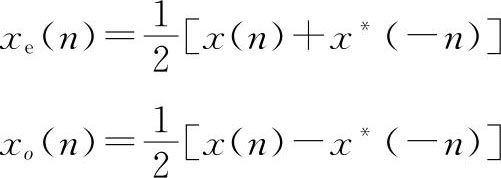
将上面两式分别进行DTFT，得到：

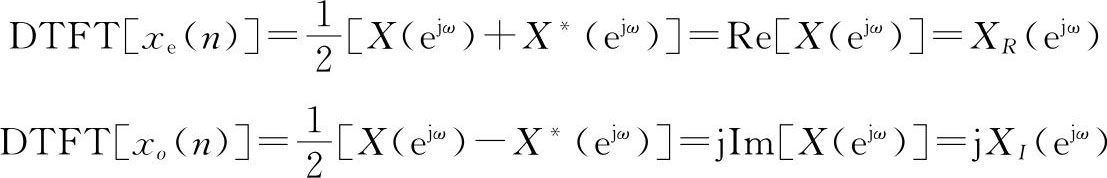
因此对x(n)进行DTFT得到：

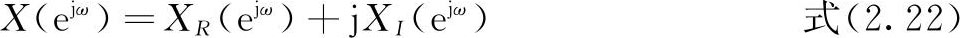
式(2.22)表示序列的共轭对称部分x

e

(n)对应着DTFT的实部X

R

(e

jω

)，而序列的共轭反对称部分x

o

(n)对应着DTFT的虚部(包括j)。

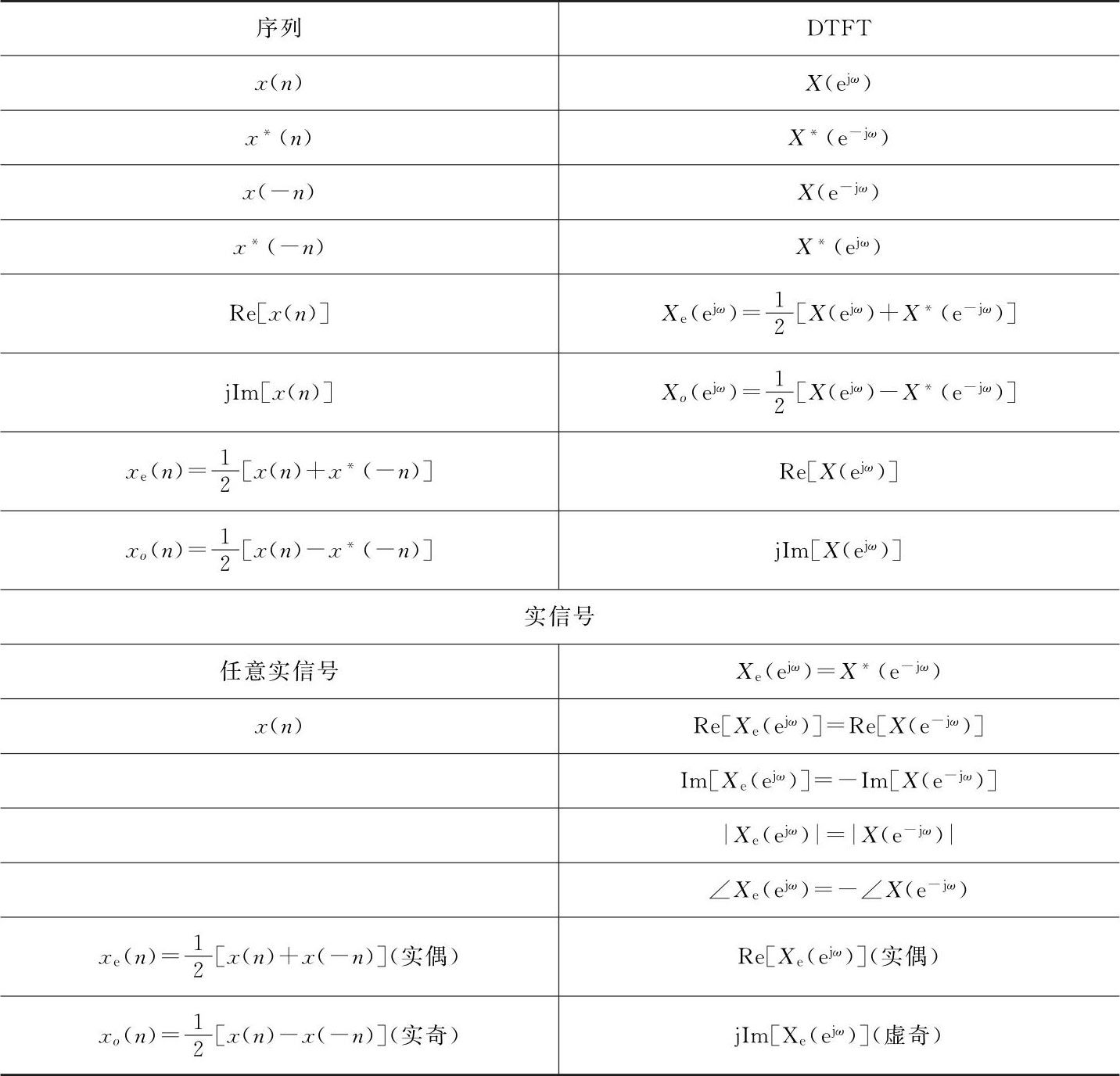
为了实际中可以利用序列对称性来简化傅里叶变换的计算，我们把上面讨论的结果概括为表2.1。

表2.1　离散时间傅里叶变换的对称性

【例2.3】

一个实信号的傅里叶变换为

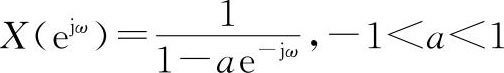
确定X(e

jω

)的实部、虚部、模和辐角，并画出当a为0.8的模和辐角的波形，从而验证对称性。

解

将X(e

jω

)分子和分母分别剩以1-ae

jω

得到：

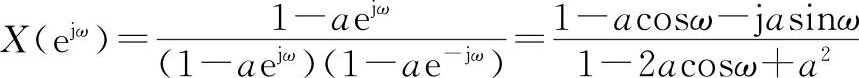
则它的实部、虚部、模和辐角分别为：

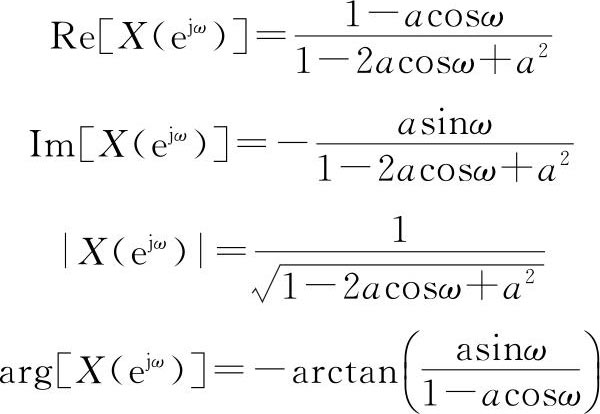
当a为0.8时实部和虚部的波形如图2.3所示。可见满足实信号谱的模和辐角的对称性。通过本例读者可自行验证实信号的谱的所有对称性都满足。

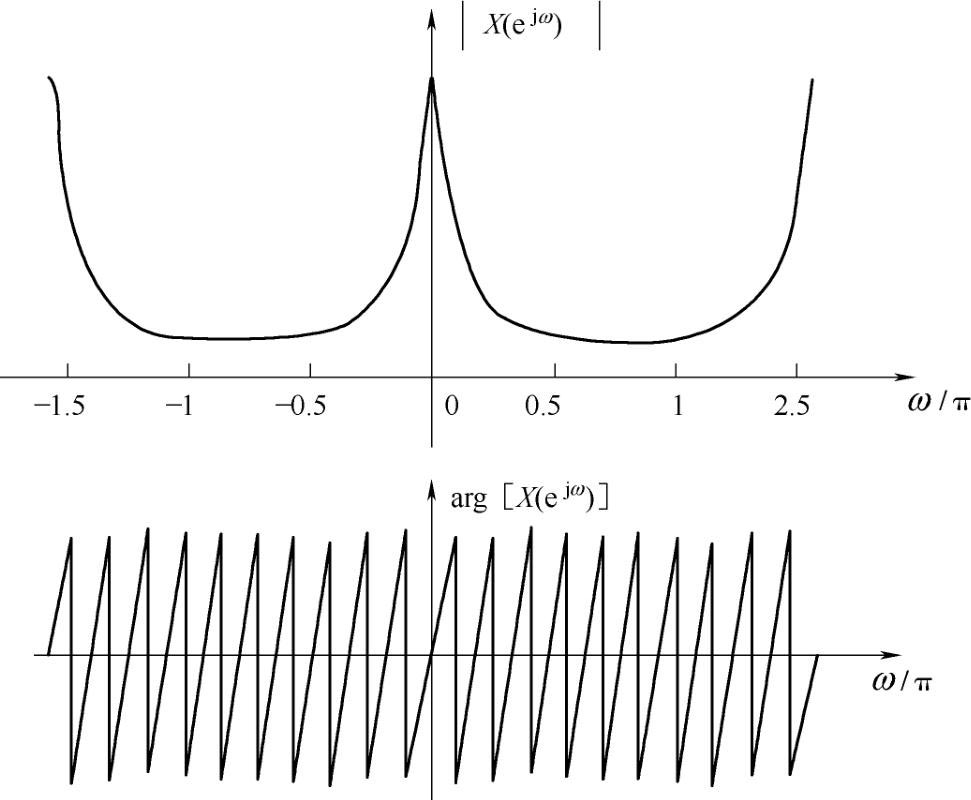
图2.3　X(e

jω

)的模和辐角图形

6.时域卷积定理

设　y(n)=x(n)*h(n)，则

证明

y(n)=x(n)*h(n)=

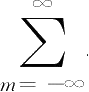
x(m)h(n-m)，那么

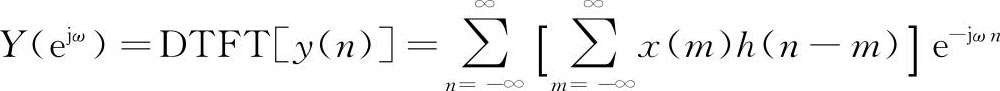
令k=n-m，则

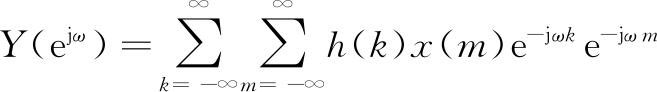
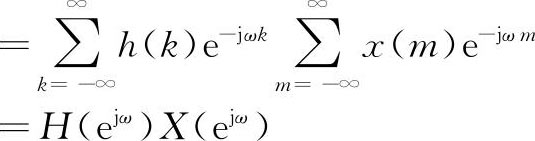
该定理说明，两序列卷积的DTFT服从相乘的关系。对于线性时不变系统，输出的DTFT等于输入信号的DTFT乘以单位采样响应的DTFT。因此，在求系统的输出信号时，可以在时域用卷积公式(1.16)计算，也可以在频域按照式(2.23)求出输出的DTFT，再作逆DTFT，求出输出信号。

【例2.4】

已知两个序列x

1

(n)=x

2

(n)={1，

1

，1}，利用时域卷积定理计算y(n)=x

1

(n)*x

2

(n)。

解

应用式(2.1)知x

1

(n)和x

2

(n)的DTFT为：

X

1

(e

jω

)=X

2

(e

jω

)=1+2cosω

那么Y(e

jω

)=X

1

(e

jω

)X

2

(e

jω

)

=(1+2cosω)

2

=3+4cosω+2cos2ω

=3+2(e

jω

+e

-jω

)+(e

j2ω

+e

-j2ω

)

所以两个序列的卷积y(n)={1，2，

3

，2，1}

7.频域卷积定理

设y(n)=x(n)h(n)，则

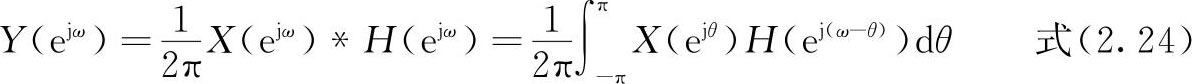
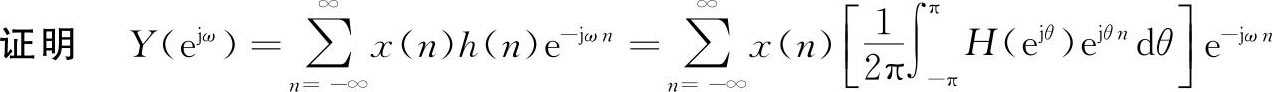
交换积分与求和的次序，得到：

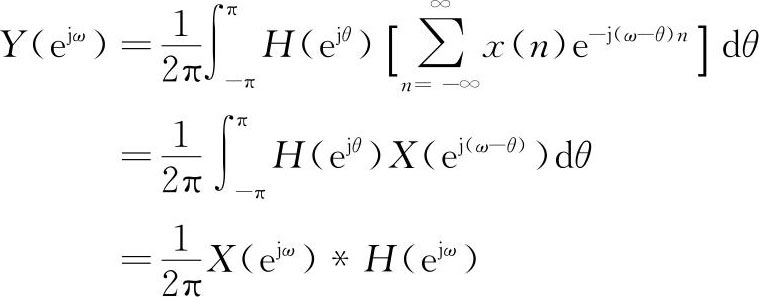
该定理表明，在时域两序列相乘，转换到频域时服从卷积关系。

8.帕斯维尔(Parseval)定理

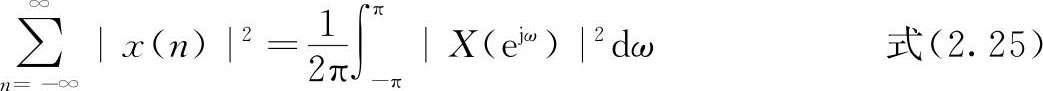
证明

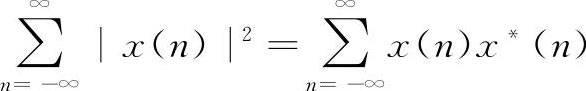
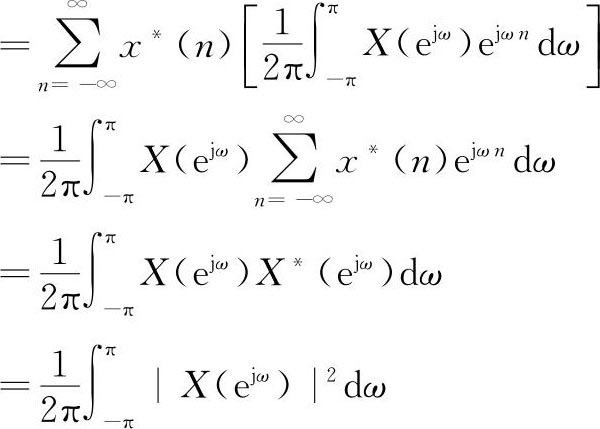
帕斯维尔定理表明了信号时域的总能量等于频域的总能量。要说明的是，这里频域总能量是指|X(e

jω

)|

2

在一个周期中的积分再乘以1/2π。

傅里叶变换的上述这些性质有利于简化运算和求解，在许多实际应用中对降低分析的复杂性是非常有用的。

at+pUZrc3iAdkcl3/N8xxmMnyEM3G5T4+Uvt1eXPACa4TuaTUvYXEKtamtXT5ca/