统计学中p值计算公式_AP选课指南：统计学

AP选课指南：统计学

01

学习理科的同学对于化学，物理，微积分等学科并不陌生。以上的学科大量学习了理论知识，对于代数运算和知识点的灵活运用要求很高。而今天我们要介绍的统计学则侧重于对于大量数据进行分析，其领域内经常涉及到结合文本的案例分析，以及实验设计；这也是一门对英文阅读有一定要求的学科。

考虑到其文理兼顾的特性，我们建议想稳拿5分的同学们在高一选考微积分AB/BC的考试，并且在高一把托福成绩提高到90+甚至100+后再在高二选考统计学。学习微积分这门相对简单的学科可以帮助同学们适应用英语学习理科知识；而托福考试则确保同学们可以从容面对大量文本。

AP Statistics MCQ

02

 我们来看一下统计学考试的基本信息：

考试总时长	180min
选择题	40题/90min
简答题A	5题/65min
简答题B	1题/25min
五分率	13%-16%
四分率	20%-23%
卷面分数	100
五分区间	70-100

统计学考试整体时间较长，难度较大。考试强烈建议使用TI-84的计算器。五分率常年在保持在15%以内(除了2020年)，在AP中算比较不友好的科目。该科目适合学习理工科(计算机，物理等)，社会科学(心理学，社会学等)，商科的同学们选考；若不是特别有兴趣，不建议学习纯人文学科(小语种，哲学等)的同学们报考，意义不大。

03

为了帮助同学们更好的决定是否选择该科目，我们带领大家大致梳理一下各单元知识点：

根据巴郎的教材，我们将考试内容分为四个部分：

Theme 1: Exploratory Analysis

Unit 1: 

Graphical Displays 统计图

Unit 2: 

Summarizing Distributions 描述分布

Unit 3: 

Comparing Distributions 比较分布

Unit 4: 

Exploring Bivariate Data 双变量数据

Unit 5:

Exploring Categorical Data 分类数据

Theme 2: Planning a Study

Unit 6: 

Methods of Data Collection

数据收集方法

Unit 7:

Planning and Conducting Surveys

设计调查

Unit 8:

Planning and Conducting Experiments

设计实验

Theme 3: Probability

Unit9:

Probability and Relative Frequency

概率和相对频率

Unit 10:

Combining Independent Random Variables

数组之间的变量

Unit 11:

Normal Distribution

正态分布

Unit 12:

Sampling Distribution

抽样分布

Theme 4: Statistical Inference

Unit 13:

Confidence Interval

置信区间

Unit 14:

Test of Significance(Proportion and Means)

假设检验(比例/平均值)

Unit 15:

Test of Significance(Chi-Square and Slope)

假设检验(卡方检验/线性回归斜率检验)

接下来我们带大家一起看一下每个主题中涉及到的内容：

Theme 1 主要学习了不同的统计图，线性回归(y=mx+b)，以及描述不同分布的方法。

我们常见的统计图有如下几类：

      

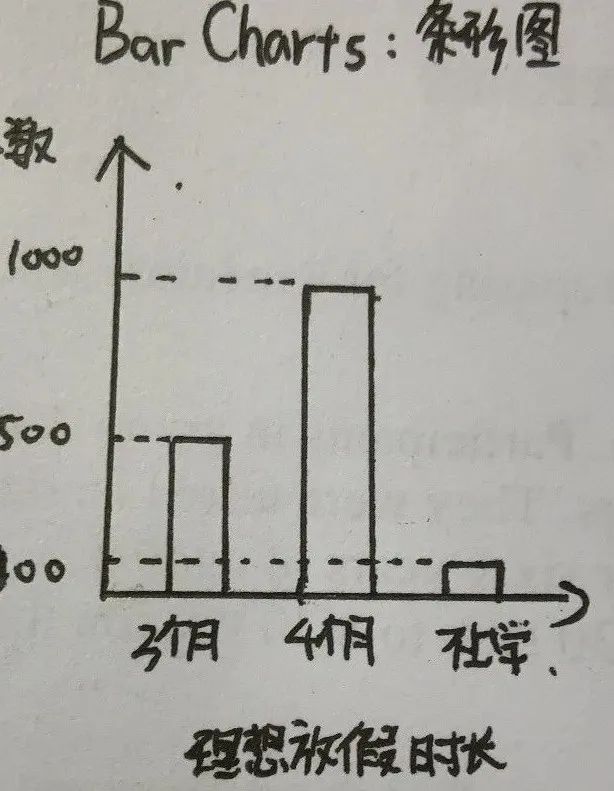
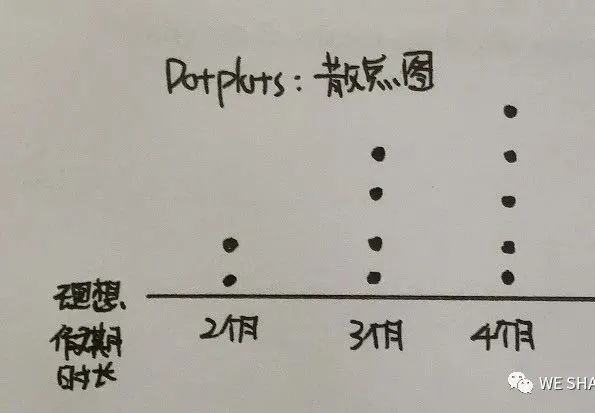
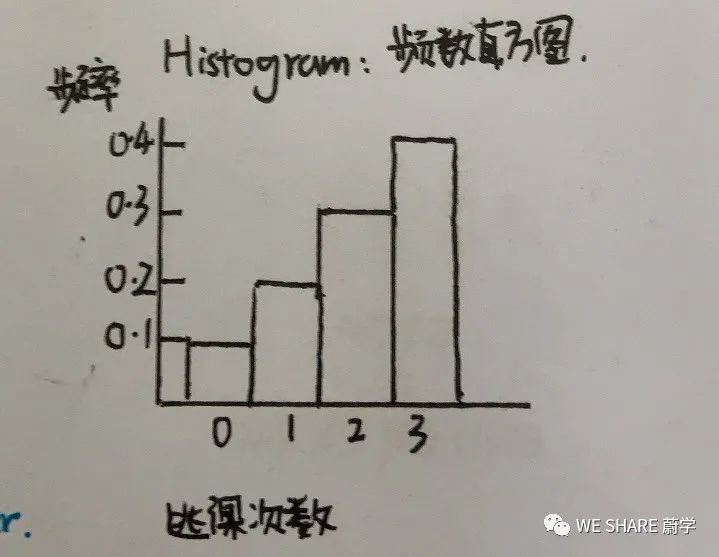
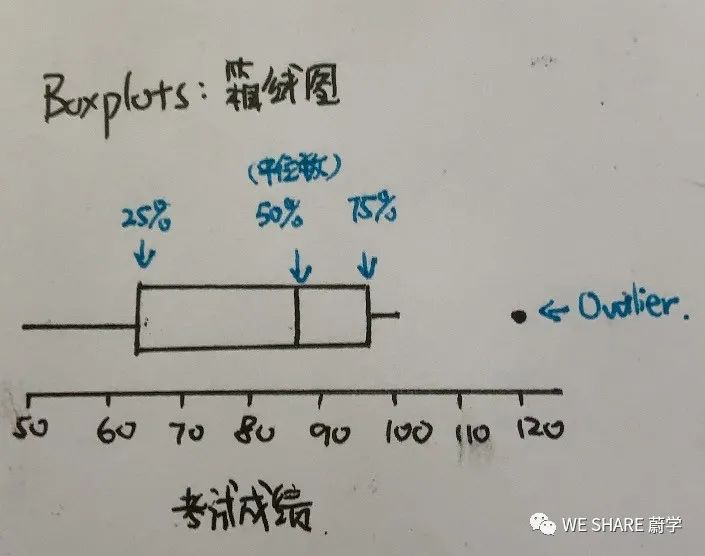
我们还要了解描述分布的三要素：Center(将图像面积一分为二)，Spread(从最小值到最大值的范围)，Shape(图像是否对称)。

描述分布

此外我们还要探究线性回归(Linear Regression),分析相关系数(r)以及其他参数。

Theme 2 理论知识较多，分析Experiment (施加影响)和 Observational Study(不施加影响)的区别(只有实验可以证明因果关系)。

这几章讲述了不同的抽样方法(Sampling Methods)，我们需要记住定义。

举个例子，Stratified Sampling和Cluster Sampling都是要利用分组选样本。二者区别在于，前者是先把总体按照某已知标准分类，在每个类别中进行随机抽样，而后者则是随机将总体分为多个组(cluster)，然后随机抽取clusters。

此外我们还要讨论研究中的bias(偏差)。偏差分析其实很有意思：如果我们在电视上做Survey，可能会导致没电视的人的意见无法被考虑，导致偏差。

最后我们为大家整理了一个实验(experiment)设计的大致流程模版：

01

Randomization 随机化(利用数字表决定受试在实验组还是对照组)

02

Single/double blinding 单/双盲 (受试/试验者不知道分组情况or具体在测什么)

03

Comparison 比较 (实验组和对照组的结果)

04

Ethical consideration(道德)

Confounding variables(无关变量)

Replication(大量样本重复实验)

Theme 3 比较偏理科。要学习基本的概率公式，两种不同的概率分布模型，以及各自的平均值，标准差计算。

两种概率

此外我们还要学习正态分布，利用计算器计算在不同区间内曲线围成的面积(来估算概率)。计算面积(算出来是具体值在所给区间内的概率)时，我们需要得知以下两个条件中的任意一个(本质相同)：

1.上下界的z-score

z=(具体值-平均值)/(标准差)

2.上下界具体值，均值，标准差。

如果我们知道一组卡车司机开车的平均驾驶时长是1000小时，标准差60小时，然后样本数量足够大可以模拟为正态分布，我们则可以很轻松计算出任意卡车司机驾驶时长在970小时和1100小时间的概率。

除了正态分布，我们还要学习t分布和Chi-Square分布。这两种分布相对复杂，主要用于利用多个样本参数来估算总体参数。难度较大，涉及到了参数计算的不同公式(标准差，平均值等)。值得注意的是，我们在分析时要注意到底分析proportion(比例)还是平均值(不同样本的平均值)；二者公式不同。

Theme 4 涉及到假设检验和置信区间，考察逻辑思维能力。

假设检验的思路是设立Null-Hypothesis(H0)，然后设立Alternative-Hypothesis (Ha)。如果计算出的p-value小于我们设定的α-value(significance level)，我们就可以有充足的证据反驳H0，证明Ha合理性。

置信区间也考察很多。我们需要学会利用公式计算Margin of error(z✖️标准差)，写出置信区间，然后解释其含义。在这部分我们需要简洁明了的用英文进行案例分析。值得注意的是(α+置信水平)=1.

置信区间基本计算公式

在有些情况下，我们使用t-score进行计算，也需要我们查表定值(t检验涉及到了自由度df，df=样本数量n-1)，t检验可以是一种超级精确的z检验。倘若z检验能够反驳H0，那么t检验也一定可以反驳H0。一般情况下在样本数量很小时，我们使用t检验(在利用样本平均值估算总体平均值会用到，即上图的Mean)。

举个例子，一个省里面所有的湿地中平均水草覆盖面积是100平方米，标准差为10平方米。我们怀疑平均面积不止100平方米。每个样本里抽20块湿地，所有样本中平均值为113平方米。我们来看一下在α=0.05时，也就是95%的置信水平得出的结论。

n=20，所以n是小样本，我们使用t检验，自由度df=20-1=19。

因为显然 20<0.1✖️(总体数量)，所以样本独立，满足t检验的条件。

我们假设： 

H0: 平均值=100

Ha：平均值>100

进行单侧t检验(我们只需要考虑大于100，所以只用算单侧)：

得出结论：

因为p值远远小于给定的α值，所以我们有充足的证据反驳H0并且95%肯定这个省里面湿地面积平均值大于100平方米.

除了以上的检验我们还会学习卡方检验以及回归直线斜率的检验。卡方检验用于具体的数据进行分析(通常有表格)，而回归直线检验的目的是确定两个变量之间是否存在关系(H0：斜率=0，Ha：斜率不等于/大于/小于0)。若我们通过上文说的检验得到的p值小于给定的α值，我们就可以确定两个变量是否独立(是否存在关系)。

附计算器使用指南：

                

点击上方蓝字，关注WE SHARE

我们是WE SHARE 蔚学

我们是一群国际高中生