一只青蛙跳向三个台阶_一只青蛙跳出来的分治法、回溯法与动态规划

本文来源于力扣圈子，作者：胡小旭，点击查看原文

力扣​leetcode-cn.com

从 2018 年 7 月份开始，基础薄弱的我从 0 开始刷力扣。目的性很明确，也很简单 —— 就是为了提高解决问题的思考实践能力，也为了提升自己的核心竞争力。也许，牛人会觉得这并不算什么竞争力。但这是我目前能做的比较基础的事情罢了。

截至 2018 年 12 月 28 日，我已经刷了 108 道题目。顺序基本上是按照面试题目出现的频率（Frequency）来刷的，这个频率在力扣上需要订阅会员后才可以看到。在刷了 108 道题目后，有一些题目会觉得 “似曾相识” ，也会有一种触类旁通的感觉。

进入正题。经过了 108 道题的历练之后，我来说说对于分治法、回溯法和动态规划的理解。

我觉得他们三者是一个相互有交集的概念，并不是相互完全独立的。至于为什么不是完全独立的，在分别阐述这三种方法的解决思路后，我们再总结一下。

一、分治法（Divide and Conquer）

分治法是解决规模庞大问题的很好思路，他通过降低问题的规模，形成若干个规模更小但形式相同的子问题，进行递归求解。在求解后，将各个子问题的解合并起来，形成原问题的解。

那么它的大致流程主要分成三步：

• 分解（Divide）将大规模的问题分解成若干个规模更小但形式相同的子问题。
• 解决（Conquer）如果当前问题的规模足够小，并可以直接解决的话，那么直接解决并返回解。否则，继续进行分解并递归求解分解后的子问题。
• 合并（Merge）将各个子问题合并，最终形成原问题的解。

所以，明确了三步之后，还要明确一件事件 —— 实现方式：递归法。

分治法一般来说会采用递归法来进行实现，当然，利用迭代法（比如 for、while）也是可以的。

所以，我们往往看到的递归算法从广义上来说都是分治法。无非就是有些递归算法将问题分解了若干个子问题，然而有些递归算法将问题分解成了一个子问题。那么有些作者会称作前者是分治法，后者是减治法。

其实，这个概念真的非常重要。在面对很多问题的时候，都可以用这种思路去思考。那么其中思考的一个非常重要的一点就是递归算法中的边界（跳出）条件的判定。

只要我们想明白了求解子问题过程中的边界条件，那么问题就会很清晰，并且很容易写出程序来。否则，模糊的边界条件，会导致整个递归算法进入到“死循环”的尴尬地步。

举个例子

青蛙 跳台阶的问题：一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法？

那么如果我们用分治法的思路思考的话，这道题真是非常容易理解。

首先，当青蛙在面对第一个台阶时，他只有两种选择 —— 跳一步还是跳两步。如果我们定义 f(n) 代表青蛙跳跃到 n 层台阶一共的方法数，那么我们可以将问题进行分解两个规模更小，但形式相同的问题：

C++

f(n) = f(n - 1) + f(n - 2)

其中 f(n-1) 是青蛙选择跳一步后，剩下的子问题，同理 f(n-2) 是青蛙选择跳两步后剩下的子问题。这样，我们就把问题进行了分解。

下面再谈谈如何解决，正如上面谈到的解决步骤，如果规模足够小那么直接返回，否则继续降低规模进行递归求解。这时，就是我们要确定边界条件——即当 n = 1 和 n = 2 时的情况。

在明确了边界条件后，合并就非常的简单，也就是简单的相加即可。

那么代码写出来是什么样子呢？

C++

#include <iostream> 
using namespace std;                                                                                                      
int f(int n) {          
// 边界条件（解决）   
if (n < 1) return 0; // 当台阶数目小于1时，那么就返回0种方案数量     
if (n == 1) return 1; // 当台阶数目为1时，问题的规模已经足够小，我们可以直接想出他的方案数量—— 即1种：1步    
if (n == 2) return 2; // 当台阶数目为2时，他的方案数量为2种，即—— 1步+1步，2步        
return f(n - 1) + f(n - 2); // 分解并合并     
}                                                                                                                                     
int main() {     
cout<<f(4)<<endl;    
return 0;           
} 

二、回溯法（Backtracking）

回溯法，我理解应该也可以叫做深度优先搜索（Depth-First Search）。所以，它是一种搜索算法。

既然谈到搜索，往往这里面会面临选择的情景。以那个青蛙为例，当面对第一个台阶时，他有两个选择。当他选择一种选择后，将“义无反顾”地一条道走下去，每层都会进行一次选择，直到走到第 n 层位置时。这时，青蛙已经触碰到了边界，并得到了一种方案，之后青蛙会返回到最近的上一次选择时的情景，选择第二种情况继续走下去。以此往复，直到搜索全部的情景。

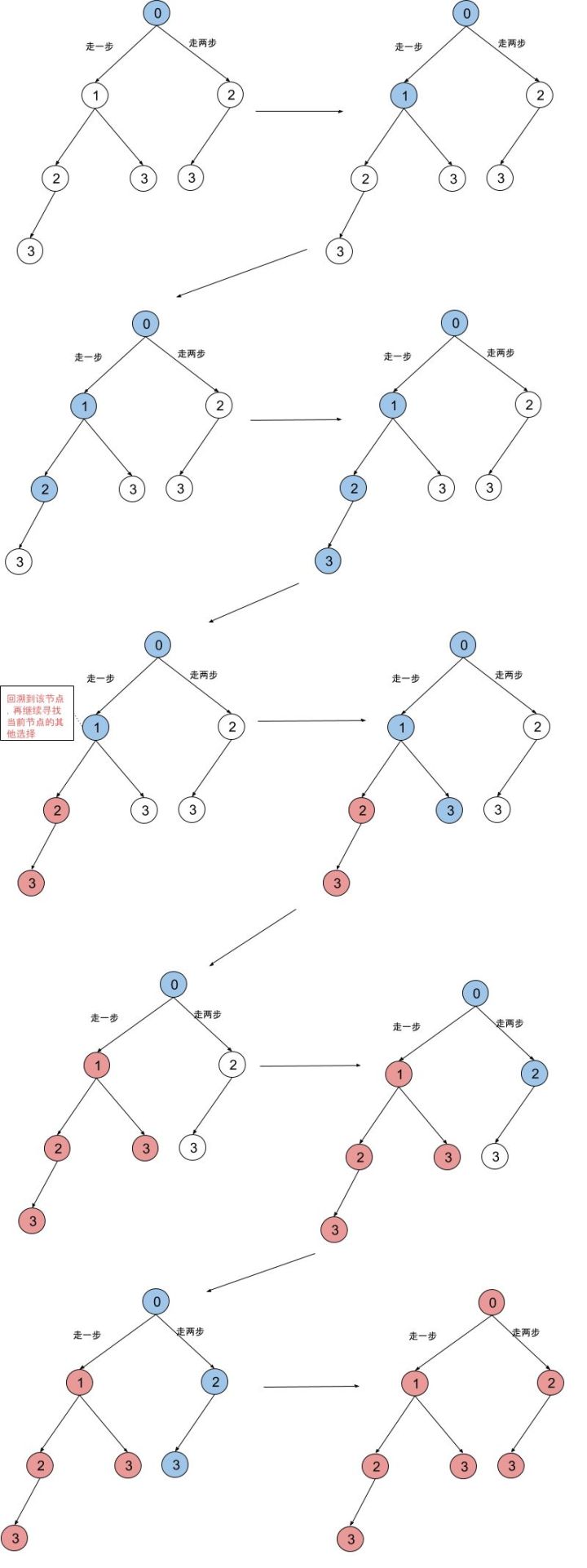
是的，这非常的抽象。我们来看看用二叉树来描述运动轨迹是怎么样的。我们假设 n = 3。

颜色

• 蓝色 代表当前搜索路走过的路径节点
• 白色 代表没有搜索走过的节点
• 红色 代表已经搜索过的节点，不可以再走

左右子树

• 左子树 代表走一步
• 右子树 代表走两步

回溯

如下图中红框标记的位置就是回溯到某一个情况。

如果你理解了下图的运动轨迹，我想差不多对于回溯的搜索过程就基本了解了。所以，你可以找到其他回溯点么？

理解了上图的运动轨迹后，那么，代码是什么样子呢？

C++

#include </iostream><iostream>                
using namespace std;                                                                                                               
/**        
 * int count 方案总数          
 * int target 目标—— 剩余的台阶数      
 */
void dfs(int& count, int target) {              
// 边界条件    
if (target < = 2) {    
        count += target; // 当剩余一个台阶是即累加一种方案，剩余两个台阶时累加两种方案             
return;        
    }                                                                                                                                
// 下面是两个基本点选择一步和选择两步        
// 选择一步      
    dfs(count, target - 1);                                                                                                                                   
// 选择两步        
    dfs(count, target - 2);     
}                                                                                                                                  
int main() {    
int count = 0;    
    dfs(count, 4);    
cout<<count<<endl;   
return 0;      
} 

边界条件

• 剩余一个台阶时，累加一种方案
• 剩余两个台阶时，累加两种方案

再说更重要的选择的两个基本点

• 选择走一步
• 选择走两步

以此进行递归搜索（深度优先搜索 DFS），在搜索到边界时进行回溯，以此往复直到搜索到所有情况为止。

三、动态规划（Dynamic Programming）

动态规划有两个重要的基本性质

最优子结构

如果一个问题的最优解包含了其中子问题的最优解，那么称其具有最优子结构的性质。

什么意思？青蛙在面对 n 台阶时的解决方案数是 f(n)，那么我们知道 f(n) = f(n-1) + f(n-2)。其中的 f(n-1) 与 f(n-2) 就是两个子问题的最优解，此时我们可以理解成一个问题的最优解包含了其子问题的最优解，那么这个时候这种问题具有了最优子结构性质。

重叠子问题

这个性质，在我理解是对于上文提到的子问题的补充说明。当解决一个问题时，往往需要依赖于其更小规模的子问题的解，甚至是同时依赖于若干个规模更小的子问题的解，即子问题是被（重复）包含于比其更大的问题中的，所以他是具有重叠子问题的性质。

在这里，多提出一句，这个子问题是在解决当前问题时需要依赖的。即只有计算了子问题，父问题才可能被求解。这是和贪心算法的重要区别所在。

状态转移方程

C++

dp[i] = dp[i - 1] + dp[i - 2]

• i 代表当前问题的规模，即所需要跳过的台阶数。
• dp[i] 代表的是跳过 i 个台阶的方案数量

其实，看到这里我们会发现，根据动态规划和分治法的思路，其解决方案大致是一样的，这一点从其递归关系式和状态转移方程可以看出来。这也是我在前文说到的，分治法与动态规划有交集的一种情况的具体体现。

那么，实现动态规划的方式一共有两种

• 递归法
• 迭代法

其中递归法与分治法的解法是一样的，那么我们用迭代法来实现动态规划的思路。

C++

#include <iostream>
#include <vector>

using namespace std;                                                                                                               
int main() {     
int n = 4;      
vector<int> dp(n + 1, 0);     
    dp[1] = 1;    
    dp[2] = 2;                                                                                                                     
for (int i = 3; i < = n; ++i) {    
        dp[i] = dp[i - 1] + dp[i - 2];       
    }                                                                                                                              
cout<<dp[n]<<endl;     
return dp[n];  
} 

总结

通过上面的分析，我们发现其相互相交的共性：

• 递归 动态规划、分治法与回溯法都可以使用递归的方式来实现
• 子问题 分治法、回溯法与动态规划都利用了子问题的解进行决策

在我理解，上面的三种方式都是面对问题时的解决思路，这个思路非常重要。因为思路并不是针对某一个问题，而是某一类问题。在面对很多问题时，如果能够尝试用这几种思路去思考，会更容易、更顺利地解决问题。

最后，留一个坑，你觉得对于寻求一个整型数组的全排列的问题，能否分别用上述的方式来解决呢？

题目：给定无序整型数组 `nums = [1,2,4,2,-2,10]`，寻找所有的排列情况。即 `An1，An2...Ann`。

本文作者：胡小旭

声明：本文归作者版权所有，如需转载请联系。文章封面图来源于网络，为非商业用途使用，如有侵权联系删除。