四阶代数余子式怎么求_七天期末线性代数急速突破——行列式篇（考试不挂）...

写在前面的话：

期末复习展开，为了方便大家更好的“预习”线性代数，考试完美过关，我们推出“七天期末线性代数急速突破栏目”

这个栏目将线性代数分为六个章节：每个章节分为两个系列：考试不挂，提升拔高

考试不挂系列是线性代数基础知识和基础习题的汇总，只要大家认真看认真学习，可以轻轻松松保证考试不挂科

提升拔高系列是线性代数拓展知识和拔高习题的汇总，难度较高，知识点更加深入，是为了让大家在期末考试突破90分冲刺满分

---

基础知识

一、行列式和矩阵的区别

行列式：是一个数值，通过对

的矩阵进行计算而得到的一个数值，

行和列不相等的矩阵是无法计算出行列式的

矩阵，是一个表格，一个由

行

列的数字组成的一个大表，矩阵的行和列是可以相等也可以不等的

二、行列式的计算方法

1、逆序数法

1）全排列

把n个不同的数排成一列，叫做这n个数的全排列（排列）。一般1,2，....，n是n个数排列的标准次序

2）逆序数

当n个数的任意排列中两个数的先后次序与标准次序不同，就说有一个逆序（如213中的21即一个逆序），一个排列中所有的逆序总数叫做这个排列的逆序数。逆序数是奇数的排列叫做奇排列，逆序数是偶数的排列叫做偶排列。将逆序数即为符号

例如：求

从左到右一个数一个数看， 3前面比它大的数有0个，3对应的逆序数为0 2前面比它大的数有1个，2对应的逆序数为1 5前面比它大的数有0个，5对应的逆序数为0 1前面比它大的数有3个，1对应的逆序数为3 4前面比它大的数有1个，4对应的逆序数为1 故

3）n阶行列式定义

对于

对于

个数组成的数表，取自不同行不同列的n个元素的乘积的代数和，逆序数为偶数时带正号，逆序数为奇数时带负号

其中

是

的一个排列，当

是偶排列时带有正号，当

为奇排列时带有负号

用逆序解答行列式的方法又可以称之为对角线法，其只适用于一二三阶行列式的计算（当阶数大于三时，对角线法则十分繁琐），如：

一阶行列式：

，如

二阶行列式：

，先左后右，先加后减

对于二阶行列式

而言，其表示的为以行向量或列向量为边围成的平行四边形的面积

三阶行列式：

三阶公式看起来比较复杂，记得时候可以这样记，首先将行列式写两遍，再用斜对角线将数字框起来，则框起来后的式子相乘后即为上式中的每一项

2、代数余子式法

1）余子式：将行列式

中元素

所在的

行元素与

列元素去掉，剩下的

行和

列元素按照原来的排列次序构成了

阶行列式，称为元素

的余子式，记为

【例题】

行列式如下，求

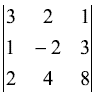
解答：

为去掉第1行第1列元素后的2阶行列式

为去掉第2行第3列元素后的2阶行列式

2）代数余子式：

为元素

的代数余子式

3）代数余子式求行列式：行列式等于行列式某行（某列）元素与其对应的代数余子式乘积的和，即

或

代数余子式的方法一般适用于4阶一下的行列式求解，大于4阶的行列式一般不建议采取此种方法

【例题】

求下列行列式

分析：

利用第一行进行展开，先求出

，再利用

求出

，再利用公式

即可求出行列式

解答：

3、化为上下三角法求解行列式

1）上下三角行列式

对于下三角行列式，其值也为对角线元素乘积

对于对角行列式，其值也为对角线元素乘积

2）行列式的性质

• 行列式和它的转置行列式是相等的

对于矩阵A，转置即矩阵A的行和列对应互换。

则

• 互换行列式某两行（列），行列式的正负性改变
• 行列式若有两行（列）完全相同，则行列式为零
• 行列式的某一行（列）都乘以同一常数
  ，等于
  乘以这个行列式（注意只能是一行或一列）
• 行列式中某一行（列）所有元素的公因子，可以提到行列式记号的外面
• 行列式中某两行（列）对应元素成比例，行列式为0
• 行列式某一行（列）元素都是两元素和，则可以拆成两个行列式的和（注意只能是一行或者一列）

若

，则

• 把行列式某一行（列）的元素k倍加到另一行（列），行列式不变

4、分块矩阵求解行列式

一个

阶行列式内部的数字可以直接进行切块，切成4个方阵，当切成后的方阵含有0矩阵，则可以采用下列计算方法进行计算如下：

---

感谢 @小季不是咸鱼 对本系列的大力支持

基本题型讲解

题型一、计算行列式

【1.1】对于形式一般的行列式，更好的方法是将该行列式转换为阶梯型，转换为三角行列式，注意行列式性质的运用

解：

先交换第一行和第二行，然后再将第一行的-2倍加到第二行，-3倍加到第三行，尝试化成阶梯型，发现第二行和第三行对应成比例，行列式等于0

【1.2】

解：

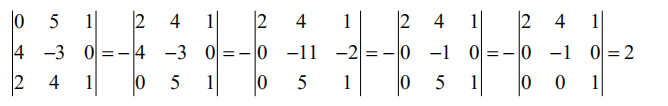
方法与上题相同，通过行变换，将其转化为三角矩阵，行列式直接等于对角线乘积

【1.3】

解：

通过上述三个例题我们可以看到，对于一个行列式，最首先想到的办法通过行变换，将其转化为三角矩阵。

题型二、利用行列式性质求解

【2.1】已知行列式

,求

（1）

（2）

（3）

解：（1）

第三行乘3,那么行列式整体就乘3

（2）

（3）

该行列式交换了第一行和第二行，行列式乘-1，又交换了第二列和第三列，行列式乘-1，最终行列式的值不变

题型三、化为上下三角法求解行列式

【3.1】每行或每列相加后为常数的行列式

求

解：

注意求行列式很常用的一种方法：当行列式各行（列）诸元素之和相等时，将各行（列）加到同一行（列）上去求和，再提公因子，然后再运用其他方法求解
本题当中，每一列的元素和都为

，故先将每一列求和，然后提取出来

【3.2】求：

解：

当遇到形式比较对称有规律的行列式，需要凭借我们的观察和试探，如果实在不行则就硬算，根据行列式的性质硬将其化为三角矩阵。求行列式必须积累一定的经验。

【3.3】

解：

除了将其他很多行加到同一行上以外，常见的还有将一行分别加到其他很多行

综上所示：求行列式的一般方法为“行和，列和相同”

行和，列和相同是指：若每一行（列）每个元素相加的和相等，如【3.1】所示

题型四、利用代数余子式求解行列式

【4.1】对代数余子式的考察

解：

---

练习题：

1.求

2.求

3.

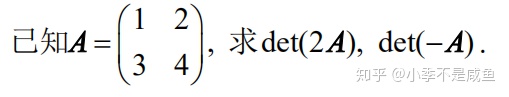
4.求行列式

5.求行列式

6.

---

写在后面的话：

知乎码字不易，更多精彩内容、练习题的答案及其解析以及技巧点拨难以更好的呈现给大家

不过大家可以抬头看一下我的个性签名，更多精彩内容等你发现

十五天期末线性代数急速突破不断更新，期待你的持续关注

喜欢的话点一下赞和关注哦