目录
二 条件随机场的概念与参数化形式(重点介绍线性链条件随机场)
3 线性链条件随机场的参数化形式(条件随机场完全由特征函数与特征函数权值确定)
一 概率无向图
1 概率无向图的概念(三段式描述)
1)大前提
联合概率分布 ,由无向图
,由无向图 表示
表示
注意:
 :表示多维随机变量
:表示多维随机变量 :表示无向图中的结点(随机变量)
:表示无向图中的结点(随机变量) :表示无向图中的边(随机变量之间的依赖关系)
:表示无向图中的边(随机变量之间的依赖关系)
2)小前提
联合概率分布 ,满足成对马尔可夫性、局部马尔可夫性、全局马尔可夫性
,满足成对马尔可夫性、局部马尔可夫性、全局马尔可夫性
3)结论
联合概率分布 ,称为概率无向图(或者称为马尔可夫随机场/马尔可夫网络)
,称为概率无向图(或者称为马尔可夫随机场/马尔可夫网络)
2 概率无向图的成对、局部、全局马尔科夫性
1)成对马尔可夫性(条件独立)
- 设
 是无向图
是无向图 中任意两个没有边连接的结点,其中结点
中任意两个没有边连接的结点,其中结点 分别对应随机变量
分别对应随机变量
- 设
 是无向图
是无向图 中除
中除 外所有的结点,其中
外所有的结点,其中 对应随机变量
对应随机变量
- 满足:

2)局部马尔可夫性(条件独立)

- 设
 是无向图
是无向图 中任意一个结点,其中结点
中任意一个结点,其中结点 分别对应随机变量
分别对应随机变量
- 设
 是与
是与 有边连接的所有的结点,其中
有边连接的所有的结点,其中 对应随机变量
对应随机变量
- 设
 是无向图
是无向图 中除
中除 外所有的结点,其中
外所有的结点,其中 对应随机变量
对应随机变量
- 满足:

3)全局马尔可夫性(条件独立)

- 设节点集合
 是在无向图
是在无向图 中被节点集合C分开的任意节点集合,其中分别对应随机变量
中被节点集合C分开的任意节点集合,其中分别对应随机变量
- 满足:

3 概率无向图的因子分解
1)团与最大团

- 团:是指无向图
 中
中 的结点子集,要求子集中任意两个结点都有边连接
的结点子集,要求子集中任意两个结点都有边连接 - 最大团:是指存在团
 ,无法添加进去任意一个结点进去
,无法添加进去任意一个结点进去
2)因子分解
第一点:因子分解的概念
概率无向图中随机变量的联合分布表示为其最大团上的随机变量的函数的乘积形式
第二点:公式

注意:
 :表示对应的随机变量
:表示对应的随机变量 :表示规范化因子
:表示规范化因子 :表示最大团
:表示最大团:表示最大团对应的随机变量
 :表示势函数(严格正函数)
:表示势函数(严格正函数)
第三点:公式的扩展
二 条件随机场的概念与参数化形式(重点介绍线性链条件随机场)
1 条件随机场的概念(三段式)
1)大前提
设 ,
, 是随机变量,
是随机变量, 是给定
是给定 条件下
条件下 的条件概率
的条件概率
2)小前提
设随机变量 构成一个由无向图
构成一个由无向图 表示的马尔可夫随机场,即满足:
表示的马尔可夫随机场,即满足: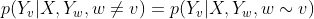
注意:
 :表示任意一个结点
:表示任意一个结点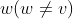 :表示除结点
:表示除结点 外的所有结点
外的所有结点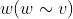 :表示与结点
:表示与结点 有边连接的所有结点
有边连接的所有结点
3)结论
称条件分布 为条件随机场
为条件随机场
注意:条件随机场本质上给定条件下的马尔可夫随机场
2 线性链条件随机场的概念(处理标注问题)

1)大前提
设 ,
, 为线性链表示的随机变量序列
为线性链表示的随机变量序列
 是给定随机变量序列
是给定随机变量序列 条件下随机变量序列
条件下随机变量序列 的条件概率
的条件概率
2)小前提
设随机变量序列 构成一个由无向图
构成一个由无向图 表示的马尔可夫随机场
表示的马尔可夫随机场
即满足: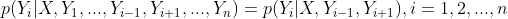
注意: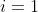 或者
或者 仅考虑单边
仅考虑单边
3)结论
称条件分布 为线性链条件随机场
为线性链条件随机场
3 线性链条件随机场的参数化形式(条件随机场完全由特征函数与特征函数权值确定)
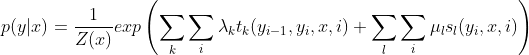
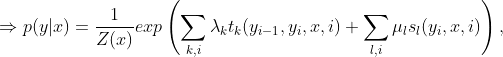

注意:
 :表示随机变量
:表示随机变量 对应的取值
对应的取值 :表示随机变量
:表示随机变量 对应的取值
对应的取值 :表示规范化因子
:表示规范化因子 :表示转移特征函数,满足转移特征条件取1,不满足取0
:表示转移特征函数,满足转移特征条件取1,不满足取0 :表示状态特征函数,满足状态特征条件取1,不满足取0
:表示状态特征函数,满足状态特征条件取1,不满足取0 :表示转移特征函数的权值
:表示转移特征函数的权值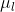 :表示状态特征函数的权值
:表示状态特征函数的权值
4 线性链条件随机场的简化形式
第一步:将转移特征函数与状态特征函数使用统一符号表示
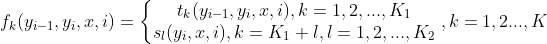
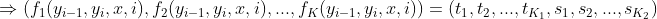
注意: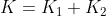
第二步:对转移特征函数与状态特征函数在各个位置求和
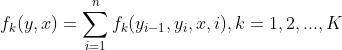
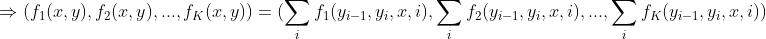
注意: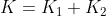
第三步:将转移特征函数的权值与状态特征函数的权值使用统一符号表示
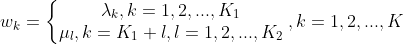
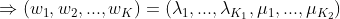
注意: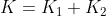
第四步:线性链条件随机场的简化形式
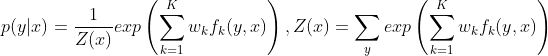
注意:令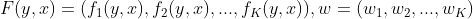
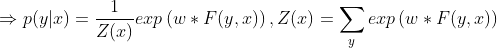
5 线性链条件随机场的矩阵形式
第一步:对观测序列
的每一个位置
,定义一个m阶矩阵(m是随机变量
的取值个数)
![M_{i}(x)=[M_{i}(y_{i-1},y_{i}|x)]](https://i-blog.csdnimg.cn/blog_migrate/d87bfd7d397b9fe36d03219be8e233f9.gif)
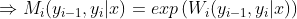
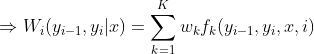
注意:我们这里引进特殊的起点和终点标记状态
第二步:非规范化的条件概率
通过对n+1个矩阵适当元素的乘积表示

第三步:规范化的条件概率

注意:理解
 表示以start为起点stop为终点通过状态的所有路径
表示以start为起点stop为终点通过状态的所有路径的非规范化概率
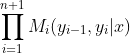 之和
之和
三 条件随机场的概率计算问题
1 概率计算问题描述
给定条件随机场 ,以及输入序列
,以及输入序列 和输出序列
和输出序列 ,计算
,计算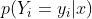 以及
以及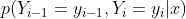
2 前向-后向算法
1)前向算法(对每个指标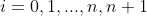 ,定义前向向量
,定义前向向量 ,维度为m)
,维度为m)
第一步:
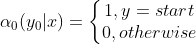
第二步:
![\alpha _{i}(y_{i}|x)=\alpha _{i-1}(y_{i-1}|x)[M_{i}(y_{i-1},y_{i}|x)],i=1,2,...,n,n+1](https://i-blog.csdnimg.cn/blog_migrate/5d56d595538c88932826f692c5b84f69.gif)
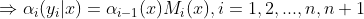
2)后向算法(对每个指标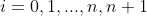 ,定义前向向量
,定义前向向量 ,维度为m)
,维度为m)
第一步:
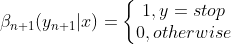
第二步:
![\beta _{i}(y_{i}|x)=[M_{i}(y_{i},y_{i+1}|x)]\beta _{i+1}(y_{i+1}|x),i=0,2,...,n](https://i-blog.csdnimg.cn/blog_migrate/4b3e41248d07ea75d933fa1b1aa94904.gif)
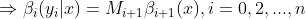
3)概率计算

![p(Y_{i-1}=y_{i-1},Y_{i}=y_{i}|x)=\frac{\alpha _{i-1}^{T}(x)M_{i}(x)\beta _{i+1}(x)}{Z(x)}=\frac{\alpha _{i-1}^{T}(y_{i-1}|x)[M_{i}(y_{i-1},y_{i}|x)]\beta _{i+1}(y_{i}|x)}{Z(x)}](https://i-blog.csdnimg.cn/blog_migrate/1c226e3887ca494dc4b233d65350228b.gif%3D%5Cfrac%7B%5Calpha%20_%7Bi-1%7D%5E%7BT%7D%28x%29M_%7Bi%7D%28x%29%5Cbeta%20_%7Bi+1%7D%28x%29%7D%7BZ%28x%29%7D%3D%5Cfrac%7B%5Calpha%20_%7Bi-1%7D%5E%7BT%7D%28y_%7Bi-1%7D%7Cx%29%5BM_%7Bi%7D%28y_%7Bi-1%7D%2Cy_%7Bi%7D%7Cx%29%5D%5Cbeta%20_%7Bi+1%7D%28y_%7Bi%7D%7Cx%29%7D%7BZ%28x%29%7D)
注意:
四 条件随机场的学习问题
1 学习问题的描述
给定训练数据集估计条件随机场模型参数的问题
2 学习问题的求解算法
1)改进的迭代尺度法
第一步:已知训练数据集,由此可知经验概率分布
,极大化训练数据的对数似然函数
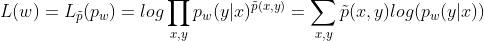
注意: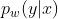 是条件随机场
是条件随机场
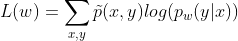
![=\sum_{x,y}\tilde{p}(x,y)log[\frac{1}{Z(x)}exp(\sum_{k=1}^{K}w_{k}f_{k}(y,x))]](https://i-blog.csdnimg.cn/blog_migrate/68b646d5e5c44599e26991903b4b6c40.gif)
![=\sum_{x,y}[\tilde{p}(x,y) \sum_{k=1}^{K}w_{k}f_{k}(y,x))-\tilde{p}(x,y)logZ(x)]](https://i-blog.csdnimg.cn/blog_migrate/a17162764274bc8a44e39f8f30d0019d.gif)
![=\sum_{j=1}^{N} \sum_{k=1}^{K}w_{k}f_{k}(y_{j},x_{j}))-\sum_{j=1}^{N} \sum_{k=1}^{K}logZ(x_{j})]](https://i-blog.csdnimg.cn/blog_migrate/41b2ca8b445eef670b0834c9f8b9e846.gif)
![\Rightarrow L(w)=\sum_{j=1}^{N} \sum_{k=1}^{K}w_{k}f_{k}(y_{j},x_{j}))-\sum_{j=1}^{N} \sum_{k=1}^{K}logZ(x_{j})]](https://i-blog.csdnimg.cn/blog_migrate/4f22c3824981e829aafc59de46935559.gif)
后续步骤有时间更新
五 条件随机场的预测问题
1 预测问题的描述
给定条件随机场 和输入序列/观测序列
和输入序列/观测序列 ,求条件概率最大的输出序列
,求条件概率最大的输出序列
2 Viterbi算法(算法原理与流程)
第一步:规范化概率最大对应的最优路径转换为非规范化概率最大对应的最优路径(减少计算量)

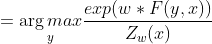
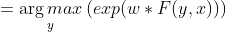
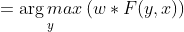
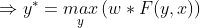
第二步:为求解最优路径,改写公式


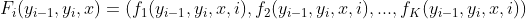


第三步:初始化(计算
的各个标记
的非规范化概率)
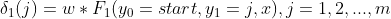
第四步:递推(
)
- 计算
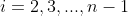 的各个标记
的各个标记 的非规范化最大概率
的非规范化最大概率
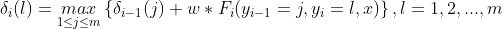
- 记录
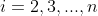 的各个标记
的各个标记 的非规范化最大概率的路径
的非规范化最大概率的路径
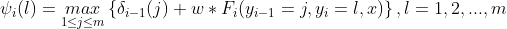
第五步:终止(
)

第六步:返回路径
第七步:最终路径








 本文深入探讨了概率无向图的概念,包括成对、局部和全局马尔科夫性,并详细介绍了条件随机场,特别是线性链条件随机场。阐述了条件随机场的参数化形式,概率计算中的前向-后向算法,以及学习问题中的迭代尺度法。此外,还讲解了Viterbi算法在预测问题中的应用。
本文深入探讨了概率无向图的概念,包括成对、局部和全局马尔科夫性,并详细介绍了条件随机场,特别是线性链条件随机场。阐述了条件随机场的参数化形式,概率计算中的前向-后向算法,以及学习问题中的迭代尺度法。此外,还讲解了Viterbi算法在预测问题中的应用。



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








