两个vector对应元素相加_Vector 和 Covector

Vector 有着明确的翻译 - 向量，如果搜索 Covector， 会把我们带到线性泛函 linear functional 的页面，可以看到：

In linear algebra, a linear form (also known as a linear functional, a one-form, or a covector) is a linear map from a vector space to its field of scalars.

Covector 看到有翻译成余向量的，也许蛮合适？毕竟 sine 、 cosine...

co 作为英文单词都前缀

• 有共同、相互、同等的意思（比如 cooperate、copartner、coequal），
• 如果用在数学上有 ‘余、补’的意思，比如 sine/cosine, tangent/cotangent, secant/cosecant。
• ‘余、补’ 其实也有点伴随、跟随的意思，比如 covarience

当然还有 coset（陪集），colatitude（余纬度），余维数（codimension），余代数（coalgebra）...

然后继续脑洞想到了共轭（conjugation）， 但是 conjugation 的前缀不是 co，而是 con- together 演化而来， conjugation 共轭家族也有很多：共轭复数（complex conjugation），共轭转置（conjugate transpose）、共轭指数(conjugate indices)... conjugation作为一般的英语单词是‘结合’，‘配合’的意思。

言归正传， 先说 Vector - 向量.

Vector

向量我们一般有三种看法：

• 一组数

向量之间可以相加， 向量还可以数乘：

这里依旧值得强调 向量本身是不变的，但在不同坐标系中的表示是不同的。Vectors are Invariant ≠ Vector components are not invariant. 就像

在用不同的基

可能是不同的。

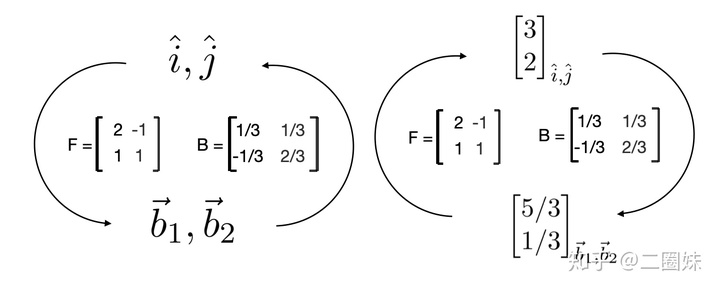
当我们有不同的基，向量写成的形式是：

同时在基变换和坐标变换 中我们写到过基变换与坐标变换有一个'相反'的关系。这种关系叫做'反变（contravariant，也称逆变）'。

在数学里，反变（contravariant，也称逆变）和共变（covariant，也称协变）描述一个向量（或更广义来说，张量）的坐标，在向量空间的基底／坐标系转换之下，会如何改变。

经常，为了更明确的表示反变，我们把分量的角标提上来，写成这种形式：

• 箭头

第二种看法是把向量看成有大小和方向的箭头，数乘和向量加法也可以和箭头的操作对应起来。不过值得注意的是并不是所有的向量都能表示为箭头，毕竟数学上很多东西都能抽象为向量，比如多项式。

• 向量空间的元素

向量可以理解成向量空间的元素， 向量空间定义为：

其中 V 是向量， S 是标量， + 和 · 是定义的加法和数乘. 基本上说来，向量就是我们可以加起来和数乘的东西。

如果需要更严格的定义可以查看 wikipedia.

Covector

那么 Covector 要怎么理解/看待呢？

• 行向量

理解成行向量并不一定准确，因为对于基正交的情况是合理的，但是对于基不正交的情况不太合理，o(╯□╰)o

• 作用于向量上的函数

把 covector 理解成向量上的函数，比如我有 covector

:

举个例子，比如我们有 covector

， 作用在向量

，其实也就是点乘：

很容易验证这个函数具有‘线性’性：

接下来的问题则是我们怎么看待它，比如 covector

, 比如作用于向量

上，我们知道结果是：

我们可以在平面上画出这个函数的等高线，再加上箭头指向等高线增加的方向：

来自 tensor for beginners

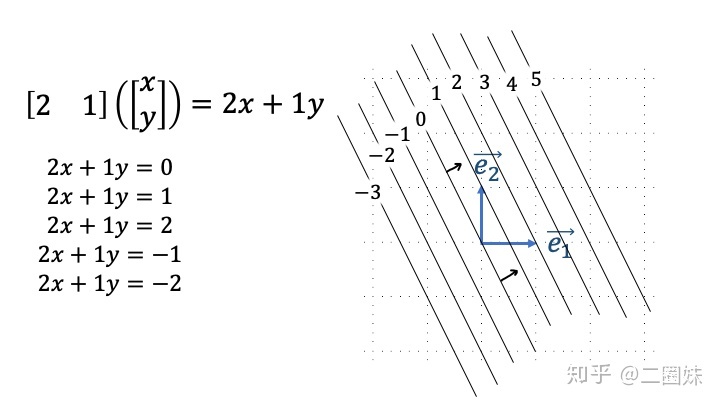
这样之后，我们甚至无需知道 covector 具体是多少，值需要看它跨过几根等高线，就知道函数作用的结果，比如下图：

来自 tensor for beginners

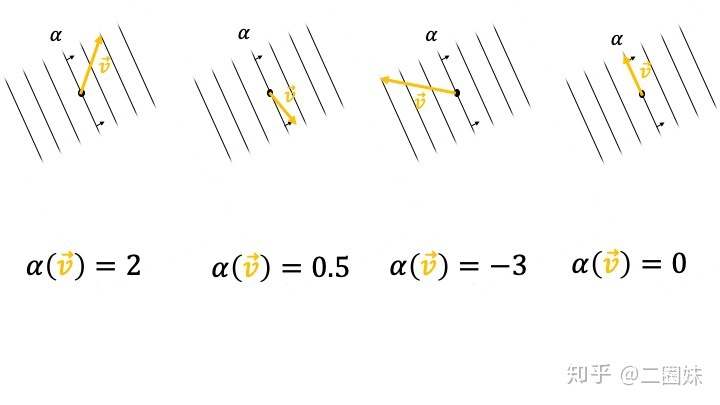
下面我们就继续利用这样的看法，同样对于 covector， 数乘和相加是怎样的效果：

数乘

来自 tensor for beginners

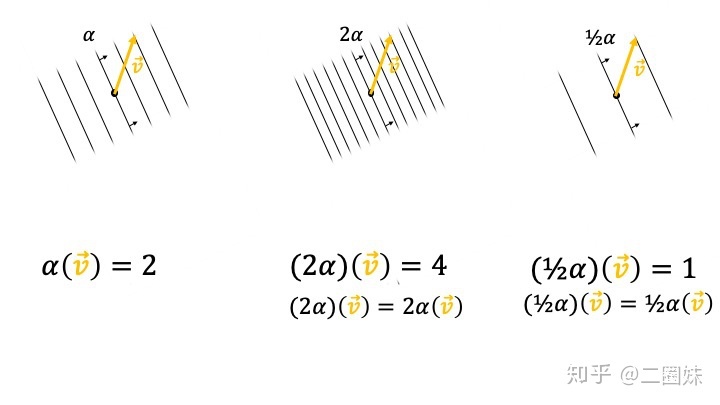
相加

来自 tensor for beginners

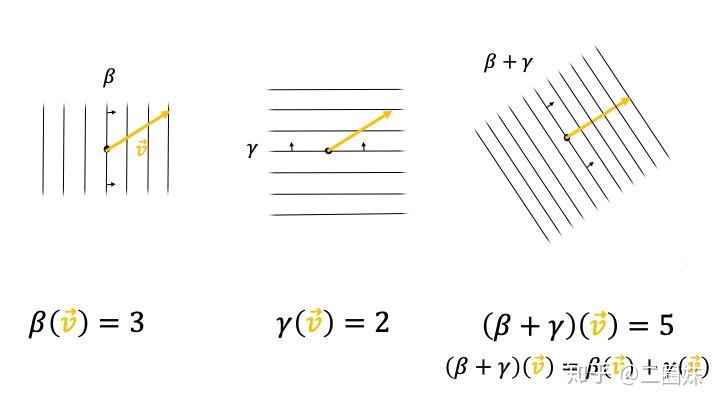
• 对偶空间中的元素

至此，给出 covector 的另一个定义，先引入'对偶空间':

对偶空间中的元素就是 covector（余向量），

. covector 本身也有加法和数乘，当然这个加法和数乘都是定义在 covector 上的：

至此 covector 定义理清，一张图总结如下：

来自 tensor for beginners

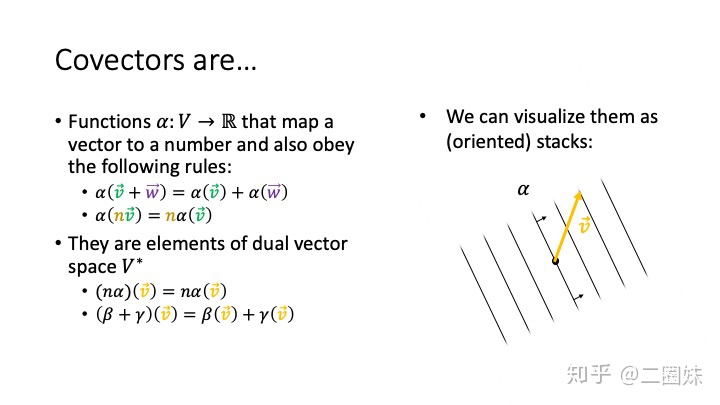
参考：

• tensor for beginners