#我要上头条# #数学# #头条教育#

01单元要点
圆是最美的图形,其中有一个非常重要的特性,就是在旋转的过程中,圆的所有性质都不变。
圆既是轴对称图形,又是中心对称图形,且其绕对称中心旋转任意角度,图形都不会发生变化。
在本单元新课学习阶段,我们已经通过实验、观察等方式,发现了圆心角、弧、弦、弦心距之间关系,明确了生活中的许多事物之间是相互联系、相互转化的。
本节内容的核心知识点是:在同圆或等圆中,圆心角相等、圆周角相等、弧相等、弦心距相等,已知其中任意一组量相等,就可以知道其他各组量也相等。
在本单元的中考考查中,围绕相关定理进行综合命题,也是考试中常见的一种方式。比如第12题,以圆周角定理为核心,融合考查了“在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半”,推论:“半圆(或直径)所对的圆周角是直角”,“90°的圆周角所对的弦是直径”等,还考查了垂径定理和平行四边形的性质。
此题的解答过程,也充分利用了圆周角定理,得到∠ACD=90°,再根据平行四边形的性质得到CD∥OB,CD=OB,则可求出∠A=30°,在Rt△AOP中利用含30度的直角三角形三边的关系可对A选项进行判断;利用OP∥CD,CD⊥AC可对C选项进行判断;利用垂径可判断OP为△ACD的中位线,则CD=2OP,原式可对B选项进行判断;同时得到OB=2OP,则可对D选项进行判断。
在中考中,任何一个考题,考查的都是我们的综合运用能力和逻辑分析能力,需要我们在学习中不断地提升这种能力,以求得数学知识的最优化。
现在,请大家走进圆的世界吧!

02阅读说明
因网页不支持数学公式,所有试题请以图片为准。
本人是一名数学教师,也是一名公益志愿者。
如果我的付出,对你或你的亲友有所帮助,期待你
(1)关注我!@同心圆数学世界
(2)在评论区留言支持!
(3)把这份资料转发给需要它的同学!
(4)你自己(亲友)能收藏用上这份资料!
(5)在本文之前和之后,已发布大量的相关复习资料,欢迎查阅使用。

03中考真题精选












04参考答案






















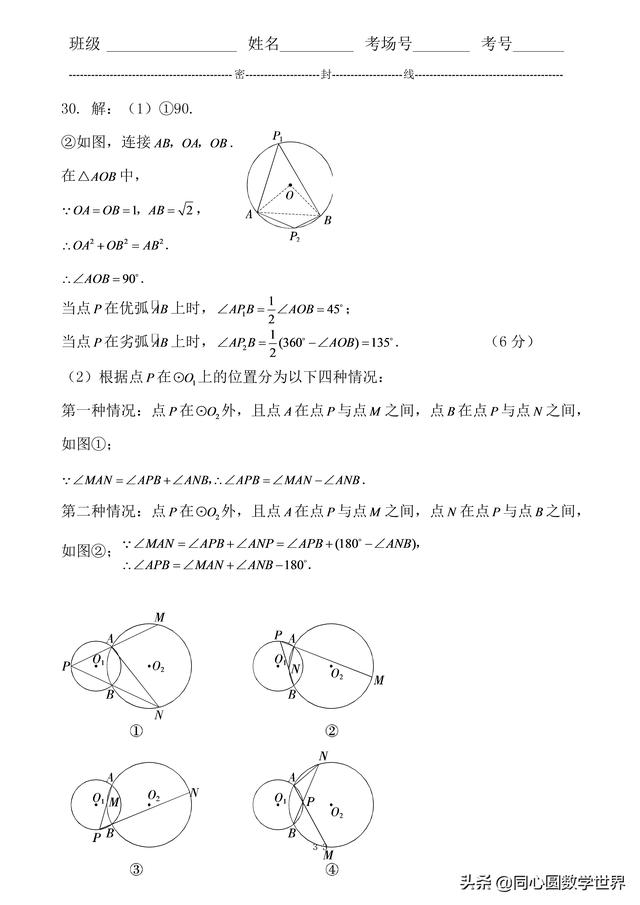


05经典题目解析
一、选择题
1. 考点圆心角、弧、弦的关系;翻折变换(折叠问题).
分析直接利用翻折变换的性质结合锐角三角函数关系得出∠BOD=30°,再利用弧度与圆心角的关系得出答案.
2. 考点M5:圆周角定理;M4:圆心角、弧、弦的关系.
分析根据圆周角定理求得∠AOB的度数,则∠AOB的度数一定不小于∠AMB的度数,据此即可判断.
3. 考点MN:弧长的计算;M5:圆周角定理.
分析连接OB、OC,利用圆周角定理求得∠BOC=60°,属于利用弧长公式l= 来计算劣弧 的长.
4. 考点M5:圆周角定理.
分析连接BD,根据直径所对的圆周角是直角,得∠ADB=90°,根据同弧或等弧所对的圆周角相等,得∠ABD=∠ACD,从而可得到∠BAD的度数.
5. 分析连接OD,由垂径定理得出AB⊥CD,由三角函数求出BH=3,由勾股定理得出DH= =4,设OH=x,则OD=OB=x+3,在Rt△ODH中,由勾股定理得出方程,解方程即可.
6. 分析先根据题意画出图形,由于点C的位置不能确定,故应分两种情况进行讨论.
7. 分析根据圆周角定理得到∠ABC=∠ADC=35°,∠ACB=90°,根据三角形内角和定理计算即可.
8. 分析根据圆周角定理可以求得∠BOD的度数,然后根据扇形面积公式即可解答本题.
9. 分析由图可知,OA=10,OD=5.根据特殊角的三角函数值求角度即可.
10. 分析根据垂径定理得出OE的长,进而利用勾股定理得出BC的长,再利用相似三角形的判定和性质解答即可.
11. 分析连接AC,如图,根据圆内接四边形的性质和圆周角定理得到∠1=∠CDA,∠2=∠3,从而得到∠3=∠CDA,所以AC=AD=5,然后利用勾股定理计算AE的长.
点评本题考查了圆内接四边形的性质:圆内接四边形的对角互补.圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角).也考查了勾股定理.
12. 分析利用圆周角定理得到∠ACD=90°,再根据平行四边形的性质得到CD∥OB,CD=OB,则可求出∠A=30°,在Rt△AOP中利用含30度的直角三角形三边的关系可对A选项进行判断;利用OP∥CD,CD⊥AC可对C选项进行判断;利用垂径可判断OP为△ACD的中位线,则CD=2OP,原式可对B选项进行判断;同时得到OB=2OP,则可对D选项进行判断.
点评此题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理和平行四边形的性质.
13. 分析根据圆心角与圆周角关系定理求出∠AOB的度数,进而由角的和差求得结果.
点评本题是圆的一个计算题,主要考查了在同圆或等圆中,同弧或等弧所对的圆心角等于它所对的圆周角的2信倍.
14. 分析连接AC,根据圆内接四边形的性质求出∠DAB,根据圆周角定理求出∠ACB、∠CAB,计算即可.
点评本题考查的是圆内接四边形的性质、圆周角定理,掌握圆内接四边形的对角互补是解题的关键.
15. 答案B.根据题意得到四边形ABCD共圆,利用圆内接四边形对角互补即可求出所求角的度数.
此题考查了圆内接四边形的性质,熟练掌握圆内接四边形的性质是解本题的关键.
二、填空题
16. 分析:连结CD如图,根据圆周角定理得到∠ACD=90°,∠D=∠B,则sinD=sinB= ,然后在Rt△ACD中利用∠D的正弦可计算出AC的长.
点评: 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了解直角三角形.
17. 考点圆周角定理;等腰三角形的性质.
分析连接AD,由圆周角定理得出∠AEB=∠ADB=90°,由等腰三角形的性质得出BD=CD,由三角形中位线定理得出OD∥AC,CE=2MD=4,求出AE,再由勾股定理求出BE即可.
18. 答案32。试题分析:由∠ABC=∠ADC=90°,E为对角线AC的中点,可知A,B,C,D四点共圆,圆心是E,直径AC然后根据圆周角定理由∠BAD=58°,得到∠BED=116°,然后根据等腰三角形的性质可求得∠EBD=32°.
考点:1、圆周角性质定理,2、等腰三角形性质
19. 分析利用垂径定理和三角函数得出∠CDO=30°,进而得出∠DOA=60°,利用圆周角定理得出∠DFA=30°即可.
20. 分析连接 并延长交 于 ,连接 ,于是得到 , ,解直角三角形即可得到结论.
点评本题考查了三角形的外接圆与外心,圆周角定理,等腰直角三角形的性质,正确的作出辅助线是解题的关键.
21. 分析先利用邻补角计算出∠BOC,然后根据圆周角定理得到∠CDB的度数.
点评本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
22. 分析连接EA,根据圆周角定理求出∠BEA,根据圆内接四边形的性质得到∠DEA+∠C=180°,结合图形计算即可.
点评:本题考查的是圆内接四边形的性质、圆周角定理,掌握圆内接四边形的对角互补是解题的关键。
23. 分析过O作OM⊥AC于M,延长MO交⊙O于P,则此时,点P到AC距离的最大,且点P到AC距离的最大值=PM,解直角三角形即可得到结论.
点评本题考查了三角形的外接圆与外心,圆周角定理,解直角三角形,正确的作出辅助线是解题的关键.
三、解答题
24. 分析(1)根据角平分线的定义和圆周角定理即可得到结论;
(2)连接OD,根据平角定义得到∠AEC=55°,根据圆周角定理得到∠ACE=90°,求得∠CAE=35°,得到∠BOD=2∠BAD=70°,根据弧长公式即可得到结论.
点评本题考查了三角形的外接圆与外心,圆周角定理,弧长的计算,正确的识别图形是解题的关键.
25. 分析连接AC,由圆心角、弧、弦的关系得出 = ,进而得出 = ,根据等弧所对的圆周角相等得出∠C=∠A,根据等角对等边证得结论.
点评本题考查了圆心角、弧、弦的关系,圆周角定理,等腰三角形的判定等,熟练掌握性质定理是解题的关键.
26. 分析(1)由AB=CD知 = ,即 + = + ,据此可得答案;
(2)由 = 知AD=BC,结合∠ADE=∠CBE,∠DAE=∠BCE可证△ADE≌△CBE,从而得出答案.
点评本题主要考查圆心角、弧、弦的关系,圆心角、弧、弦三者的关系可理解为:在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.
27. 分析(1)根据角平分线的定义和圆周角定理即可得到结论;
(2)连接 ,根据平角定义得到 ,根据圆周角定理得到 ,求得 ,得到 ,根据弧长公式即可得到结论.
点评本题考查了圆周角定理,三角形的外接圆与外心,弧长的计算,正确的识别图形是解题的关键.
29. 分析(1)由Rt△ACB中∠ABC=45°,得出∠BAC=∠ABC=45°,根据圆周角定理得出∠AEC=∠ABC,∠BEC=∠BAC,等量代换得出∠AEC=∠BEC,即EC平分∠AEB;
(2)设AB与CE交于点M.根据角平分线的性质得出 = .易求∠BAD=30°,由直径所对的圆周角是直角得出∠AEB=90°,解直角△ABE得到AE= BE,作AF⊥CE于F,BG⊥CE于G.证明△AFM∽△BGM,根据相似三角形对应边成比例,进而求出 .
点评本题考查了相似三角形的判定与性质,圆周角定理,锐角三角函数定义,通过作辅助线是解题的关键.
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








