可能存在无限递归_必备算法：递归！

递归是一种非常重要的算法思想，无论你是前端开发，还是后端开发，都需要掌握它。在日常生活中，统计文件夹大小、解析 xml 文件等等，都需要用到递归算法。它太基础太重要了，这也是为什么面试的时候，面试官经常让我们手写递归算法。本文将跟大家一起深入挖掘一下递归算法！

• 什么是递归？

• 递归的特点

• 递归与栈的关系

• 递归应用场景

• 递归解题思路

• LeetCode 案例分析

• 递归可能存在的问题以及解决方案

什么是递归？ 递归，在计算机科学中是指一种通过重复，将问题分解为同类的子问题而解决问题的方法。简单来说， 递归表现为函数调用函数本身。在知乎看到一个比喻递归的例子，个人觉得非常形象，大家看一下：

递归最恰当的比喻，就是查词典。我们使用的词典，本身就是递归，为了解释一个词，需要使用更多的词。当你查一个词，发现这个词的解释中某个词仍然不懂，于是你开始查这第二个词，可惜，第二个词里仍然有不懂的词，于是查第三个词，这样查下去，直到有一个词的解释是你完全能看懂的，那么递归走到了尽头，然后你开始后退，逐个明白之前查过的每一个词，最终，你明白了最开始那个词的意思。

来试试水，看一个递归的代码例子，如下：

public int sum(int n) {    if (n <= 1) {        return 1;    }     return sum(n - 1) + n; }

递归的特点实际上，递归有两个显著的特征， 终止条件 和 自身调用：

• 自身调用：原问题可以分解为子问题，子问题和原问题的求解方法是一致的，即都是调用自身的同一个函数。

• 终止条件：递归必须有一个终止的条件，即不能无限循环地调用本身。

结合以上 demo 代码例子，看下递归的特点： 递归与栈的关系递归的过程，可以理解为出入栈的过程。以上代码例子计算 sum(n=3) 的出入栈图如下： 为了更容易理解一些，我们来看一下函数 sum(n=5) 的递归执行过程，如下：

• 计算 sum(5) 时，先 sum(5) 入栈，然后原问题 sum(5) 拆分为子问题 sum(4)，再入栈，直到终止条件 sum(n=1)=1，就开始出栈。

• sum(1) 出栈后，sum(2) 开始出栈，接着 sum(3)...

• 最后呢，sum(1) 就是后进先出，sum(5) 是先进后出，因此递归过程可以理解为栈出入过程啦~

递归的经典应用场景哪些问题我们可以考虑使用递归来解决呢？即递归的应用场景一般有哪些呢？

• 阶乘问题

• 二叉树问题

• 汉诺塔问题

• 斐波那契数列

• 快速排序、归并排序(分治算法体现递归)

• 遍历文件，解析 xml 文件

递归解题思路解决递归问题一般就 三步曲，分别是：

• 第一步，定义函数功能
• 第二步，寻找递归终止条件
• 第三步，递推函数的等价关系式

这个递归解题三板斧理解起来有点抽象，我们拿阶乘递归例子来喵喵~ 定义函数功能定义函数功能，就是说，你这个函数是干嘛的，做什么事情，换句话说，你要知道递归原问题是什么呀？比如你需要解决阶乘问题，定义的函数功能就是 n 的阶乘，如下：

//n的阶乘(n为大于0的自然数)int factorial (int n){}

寻找递归终止条件递归的一个典型特征就是必须有一个终止的条件，即不能无限循环地调用本身。所以，用递归思路去解决问题的时候，就需要寻找递归终止条件是什么。比如阶乘问题，当 n=1 的时候，不用再往下递归了，可以跳出循环啦，n=1 就可以作为递归的终止条件，如下：

//n的阶乘(n为大于0的自然数)int factorial (int n){    if(n==1){      return 1;    }}

递推函数的等价关系式 递推的本义，就是原问题可以拆为同类且更容易解决的子问题，即原问题和子问题都可以用同一个函数关系表示。 递推函数的等价关系式，这个步骤就等价于寻找原问题与子问题的关系，如何用一个公式把这个函数表达清楚。阶乘的公式就可以表示为 f(n)=n*f(n-1)，因此，阶乘的递归程序代码就可以写成这样，如下：

int factorial (int n){    if(n==1){      return 1;    }    return n * factorial(n-1);}

注意啦，不是所有递推函数的等价关系都像阶乘这么简单，一下子就能推导出来。需要我们多接触，多积累，多思考，多联系递归题目滴~ LeetCode 案例分析来分析一道 LeetCode 递归的经典题目吧

原题链接在这里哈：https://leetcode-cn.com/problems/invert-binary-tree/

题目：翻转一棵二叉树。输入：

     4   /   \  2     7 / \   / \1   3 6   9

输出：

    4   /   \  7     2 / \   / \9   6 3   1

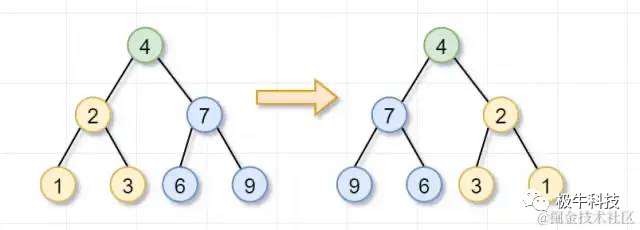
我们按照以上递归解题的三板斧来： 定义函数功能函数功能(即这个递归原问题是)，给出一棵树，然后翻转它，所以，函数可以定义为：

//翻转一颗二叉树public TreeNode invertTree(TreeNode root) {}/** * Definition for a binary tree node. * public class TreeNode { *     int val; *     TreeNode left; *     TreeNode right; *     TreeNode(int x) { val = x; } * } */

寻找递归终止条件
这棵树什么时候不用翻转呢？当然是当前节点为 null 或者当前节点为叶子节点的时候啦。因此，加上终止条件就是：

//翻转一颗二叉树public TreeNode invertTree(TreeNode root) {    if(root==null || (root.left ==null && root.right ==null)){       return root;    }}

递推函数的等价关系式原问题是你要翻转一棵树，是不是可以拆分为子问题，分别翻转它的左子树和右子树？子问题是翻转它的左子树，是不是又可以拆分为，翻转它左子树的左子树以及它左子树的右子树？然后一直翻转到叶子节点为止。看图理解一下咯~ 首先，你要翻转根节点为 4 的树，就需要翻转它的左子树(根节点为 2)和右子树(根节点为 7)。这就是递归的 递的过程啦 然后呢，根节点为 2 的树，不是叶子节点，你需要继续翻转它的左子树(根节点为 1)和右子树(根节点为 3)。因为节点 1 和 3 都是叶子节点了，所以就返回啦。这也是递归的 递的过程： 同理，根节点为 7 的树，也不是叶子节点，你需要翻转它的左子树(根节点为 6)和右子树(根节点为 9)。因为节点 6 和 9 都是叶子节点了，所以也返回啦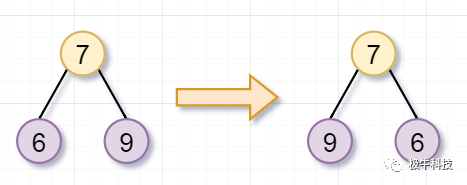： 左子树(根节点为 2)和右子树(根节点为 7)都被翻转完后，这几个步骤就 归了，即递归的归过程，翻转树的任务就完成了： 显然， 递推关系式就是：

invertTree(root)= invertTree(root.left) + invertTree(root.right);

于是，很容易可以得出以下代码：

//翻转一颗二叉树public TreeNode invertTree(TreeNode root) {    if(root==null || (root.left ==null && root.right ==null){       return root;    }    //翻转左子树    TreeNode left = invertTree(root.left);    //翻转右子树    TreeNode right= invertTree(root.right);}

这里代码有个地方需要注意，翻转完一棵树的左右子树，还要交换它左右子树的引用位置：

root.left = right;root.right = left;

因此，LeetCode 这个递归经典题目的终极解决代码如下：

class Solution {    public TreeNode invertTree(TreeNode root) {         if(root==null || (root.left ==null && root.right ==null)){           return root;         }         //翻转左子树         TreeNode left = invertTree(root.left);         //翻转右子树         TreeNode right= invertTree(root.right);         //左右子树交换位置~         root.left = right;         root.right = left;         return root;    }}

拿终极解决代码去 LeetCode 提交一下，通过啦~ 递归存在的问题

• 递归调用层级太多，导致栈溢出问题
• 递归重复计算，导致效率低下

栈溢出问题

• 每一次函数调用在内存栈中分配空间，而每个进程的栈容量是有限的；

• 当递归调用的层级太多时，就会超出栈的容量，从而导致调用栈溢出；

• 其实，我们在前面小结也讨论了，递归过程类似于出栈入栈，如果递归次数过多，栈的深度就需要越深，最后栈容量真的不够了。

代码例子如下：

/** * 递归栈溢出测试 */public class RecursionTest {    public static void main(String[] args) {        sum(50000);    }    private static int sum(int n) {        if (n <= 1) {            return 1;        }        return sum(n - 1) + n;    }}

运行结果：

Exception in thread "main" java.lang.StackOverflowError at recursion.RecursionTest.sum(RecursionTest.java:13)

怎么解决这个栈溢出问题？首先需要 优化一下你的递归，真的需要递归调用这么多次吗？如果真的需要，先稍微 调大 JVM 的栈空间内存，如果还是不行，那就需要弃用递归， 优化为其它方案了~ 重复计算，导致程序效率低下我们再来看一道经典的青蛙跳阶问题：一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。绝大多数读者朋友，很容易就想到以下递归代码去解决：

class Solution {    public int numWays(int n) {    if (n == 0){       return 1;     }    if(n <= 2){        return n;    }    return numWays(n-1) + numWays(n-2);    }}

但是呢，去 LeetCode 提交一下，就有问题啦，超出时间限制了： 为什么超时了呢？递归耗时在哪里呢？先画出 递归树看看：

• 要计算原问题 f(10)，就需要先计算出子问题 f(9) 和 f(8)
• 然后要计算 f(9)，又要计算出子问题 f(8) 和 f(7)，以此类推
• 一直到 f(2) 和 f(1)，递归树才终止

我们先来看看这个递归的时间复杂度吧， 递归时间复杂度 = 解决一个子问题时间*子问题个数

• 一个子问题时间 = f(n-1) + f(n-2)，也就是一个加法的操作，所以复杂度是 O(1)；
• 问题个数 = 递归树节点的总数，递归树的总结点 = 2^n-1，所以复杂度是 O(2^n)。

因此，青蛙跳阶，递归解法的时间复杂度 = O(1) * O(2^n) = O(2^n)，就是指数级别的，爆炸增长的， 如果 n 比较大的话，超时很正常了。回过头来，你仔细观察这棵递归树，你会发现存在 大量重复计算，比如 f(8) 被计算了两次，f(7) 被重复计算了 3 次……所以这个递归算法低效的原因，就是存在大量的重复计算！那么，怎么解决这个问题呢？既然存在大量的重复计算，那么我们可以先把计算好的答案存下来，即造一个备忘录，等到下次需要的话，先去 备忘录查一下，如果有，就直接取就好了，备忘录没有才再计算，那就可以省去重新重复计算的耗时啦！这就是 带备忘录的解法。我们来看一下 带备忘录的递归解法吧~
一般使用一个数组或者一个哈希 map 充当这个 备忘录。假设 f(10) 求解加上 备忘录，我们再来画一下递归树： 第一步，f(10) = f(9)+f(8)，f(9) 和 f(8) 都需要计算出来，然后再加到备忘录中，如下： 第二步，f(9) = f(8)+f(7)，f(8) = f(7)+f(6)，因为 f(8) 已经在备忘录中啦，所以可以省掉，f(7) 和 f(6) 都需要计算出来，加到备忘录中~ 第三步，f(8) = f(7)+f(6)，发现 f(8)、f(7)、f(6) 全部都在备忘录上了，所以都可以剪掉。 所以呢，用了备忘录递归算法，递归树变成光秃秃的树干喽，如下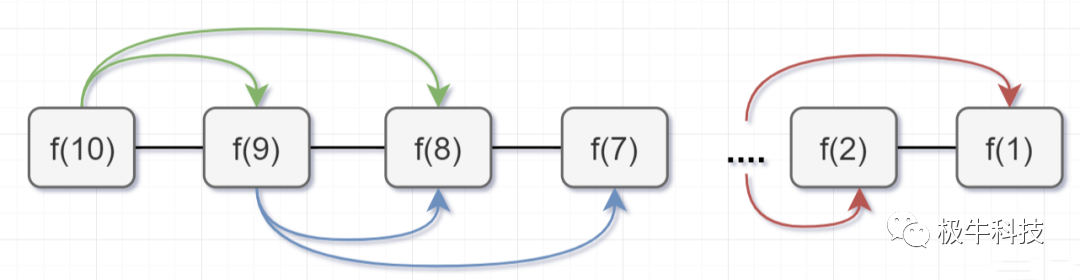： 带备忘录的递归算法，子问题个数 = 树节点数 = n，解决一个子问题还是 O(1)，所以 带备忘录的递归算法的时间复杂度是 O(n)。接下来呢，我们用带备忘录的递归算法去撸代码，解决这个青蛙跳阶问题的超时问题，代码如下：

public class Solution {    //使用哈希map，充当备忘录的作用    Map tempMap = new HashMap();    public int numWays(int n) {        // n = 0 也算1种        if (n == 0) {            return 1;        }        if (n <= 2) {            return n;        }        //先判断有没计算过，即看看备忘录有没有        if (tempMap.containsKey(n)) {            //备忘录有，即计算过，直接返回            return tempMap.get(n);        } else {            // 备忘录没有，即没有计算过，执行递归计算,并且把结果保存到备忘录map中，对1000000007取余(这个是leetcode题目规定的)            tempMap.put(n, (numWays(n - 1) + numWays(n - 2)) % 1000000007);            return tempMap.get(n);        }    }}

去 LeetCode 提交一下，如图，稳了：

参考与感谢

• [一文学会递归解题] (https://mp.weixin.qq.com/s/Hew44D8rdXb3pf8mZGk67w)
• [动态规划详解] (https://mp.weixin.qq.com/s/1V3aHVonWBEXlNUvK3S28w)

各位程序员大佬们，请让我听到你们的声音！不管你是前端开发、后端研发、测试开发、移动端开发、全栈工程师、运维工程师、网络工程师、架构师、研发经理还是其他职位，不管你在做 Android 开发 、iOS 开发、U3D 、COCOS2DX、 自动化测试、功能测试、性能测试、白盒测试、灰盒测试、黑盒测试、ETL、数据仓库、数据开发、数据挖掘、数据分析、数据架构、算法研究、精准推荐、分布式、系统集成、地图引擎、人工智能、大数据、深度学习、机器学习、图像处理、图像识别、语音识别、语音学习、机器视觉、自然语言处理、视频开发、区块链还是其它技术支持。欢迎在评论中踊跃发表意见！

扫码关注我们

极牛科技公众号

微信号 : jnkjnl

博客：niuzhendong.com

Github：github.com/niuzhendonglm

点个赞再走嘛！