19年重庆中考A卷难度相当高,尤其最后一道大题更是难上加难,二次函数+几何+动点+图形旋转的综合大题,如果将全国各地中考压轴大题难度排名,重庆A卷绝对榜上有名。
一般来说,各地中考的最后一道大题,第一问是求二次函数的解析式,这一步会给出几个点的坐标,让考生算出解析式,这是送分题。而重庆A卷的压轴大题干脆连送分小问都没有,直接上高难题。就让我们一起来看看重庆A卷的压轴题吧。
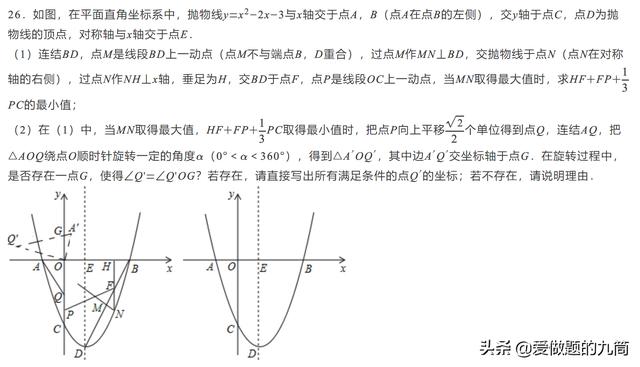
第一问的第一个难点是要了解MN什么时候取得最大值。官方答案上是通过分析三角形DNB的面积来推出当NF最大时,MN取得最大值。其实还有一个更简单的分析方法,因为直线BD与直线HF是垂直关系,因此角MFN的大小是不变的,即三角形MNF是一个角度固定的三角形。通过三角函数简单分析即可知当NF取最大时,MN取最大值。由于N在函数上,即可列出NH长度的二次函数表达式,也可以求出最大值。
第一问的第二个难点是要知道HF+FP+1/3PC的最小值。HF的值在第一问中已经可以求得,是定值2。因此本问转化为求FP+1/3PC的最小值,但是如何处理1/3PC?需要构造一个角度,使其正弦值等于1/3。即在x轴上取点K,将1/3PC转化为PJ。
第二问的难点在于如何理解角Q‘=角Q’OG,本问只需要知道直角三角形中,斜边上的中线等于斜边的一半,即在AQ上取一点G,而G恰好为AQ中点即可。因此这道题有4个答案,分别于AQ的中点G恰好过x轴和y轴的正负半轴即可。
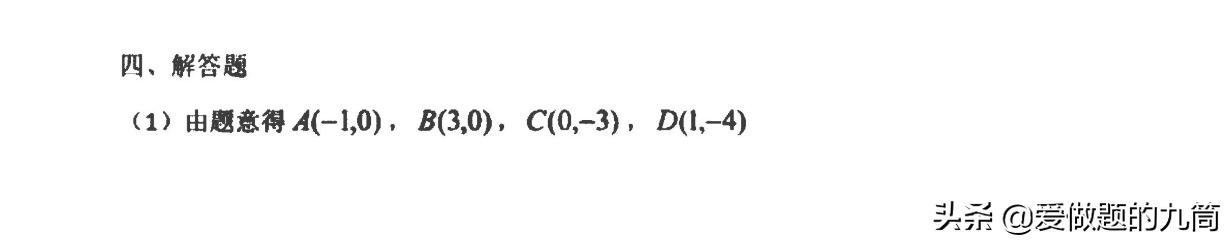








 这篇博客详细分析了2019年重庆中考A卷数学压轴题的难度和解题策略。题目结合了二次函数、几何、动点和图形旋转,挑战性强。第一问探讨了MN取得最大值的条件,通过三角函数简化问题。第二问则涉及HF+FP+1/3PC最小值的求解,利用角度构造解决。博主提供了不同于官方答案的解题思路,并解释了如何利用直角三角形性质简化问题。
这篇博客详细分析了2019年重庆中考A卷数学压轴题的难度和解题策略。题目结合了二次函数、几何、动点和图形旋转,挑战性强。第一问探讨了MN取得最大值的条件,通过三角函数简化问题。第二问则涉及HF+FP+1/3PC最小值的求解,利用角度构造解决。博主提供了不同于官方答案的解题思路,并解释了如何利用直角三角形性质简化问题。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








