简支梁挠度计算公式推导_桥梁动挠度理论分析

桥梁动挠度理论分析

1 截面位移公式

挠度作为变形的一种描述形式，可以评价桥梁质量及运营状态，反映桥梁的刚度，是桥梁整体变形最明显的反应。

截面的挠度即梁横截面的形心沿垂直于梁轴线方向的位移，是衡量梁变形的基本量之一。结构产生位移的因素有很多，如荷载、温度变化、支座位移等等。在材料服从胡克定律、结构小变形和连接处无摩擦三个假定的前提下，应用结构力学的方法，推导结构在荷载作用下的位移公式。由虚功原理可知，变形体系的虚功方程为：

从上式可以看出，结构的位移主要由荷载、材料属性和结构特性三方面决定。在荷载不变的前提下，位移的改变可以看作是材料属性、结构特性之一或两者的变化。分别计算弯矩、轴力、剪力引起的梁位移，可知弯曲变形对位移的影响是最主要的，则位移计算公式一般可以忽略轴向变形和剪切变形的影响，仅考虑弯曲变形，则梁的位移计算公式可简化为：

定义材料的弹性模量与截面惯性矩的乘积 EI 为结构的刚度，由公式（3-4）可知，在结构形式和荷载不变的情况下计算的结构位移是对结构刚度最好的反应。

2 动挠度理论

桥梁动挠度是对桥梁刚度最为实时的反应，也是桥梁在车辆荷载作用下最为真实的反应。通过对动挠度进行数值分析，可以得到车辆荷载的冲击系数和桥梁结构的内力分布情况，从而对桥梁的整体性和劣化部位做出判断。

虽然在一般情况下，对结构进行设计和分析时，静力问题是首先要面对的方面，而且是主要方面；但是有时动力荷载引起的破坏却是致命性的，是导致结构损坏的主要原因。对结构进行动力分析，确定结构在动荷载作用下的内力和变形，从而确定结构的动力特性，是结构动力分析的最终目的。1905 年俄国学者 Kphnob首先研究了在匀速常量力作用下简支梁的振动问题，在车辆质量与桥梁质量比较小的情况下（例如较大跨度的公路桥梁），可以给出动力响应的近似解。

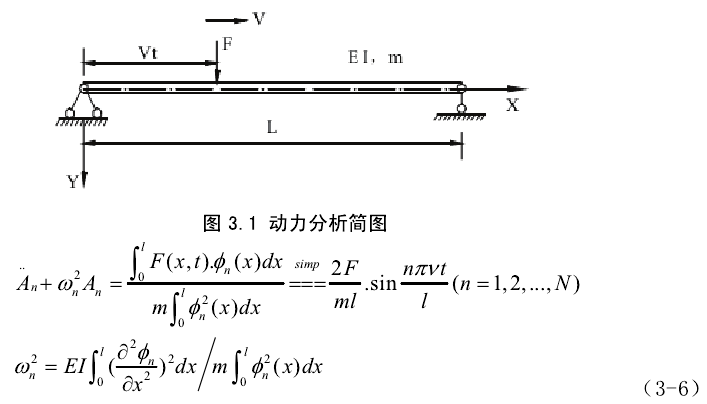
如图 3.1 所示，简支梁作用匀速常量力 F，速度为 V。时间 t=0 时，常量力 F位于左侧支承处；t 时刻，常量力 F 位于距离左侧支承 vt 处。假定 EI、m 均为常数，则简支梁在外荷载 F(x,t)作用下的振动方程可表示为：

《来源于科技文献，经本人分析整理，以技术会友，广交天下朋友》